ЗапуститьVS, со стартовой страницы; перейти к созданию проекта; в качестве типа проекта указать тип Библиотека классов ( ClassLibrary). В открывшемся окне создания DLL, показанном на рис. 4.1.2-2, все поля заполнены значениями по умолчанию. Как правило, их следует переопределить, задавая собственную информацию.

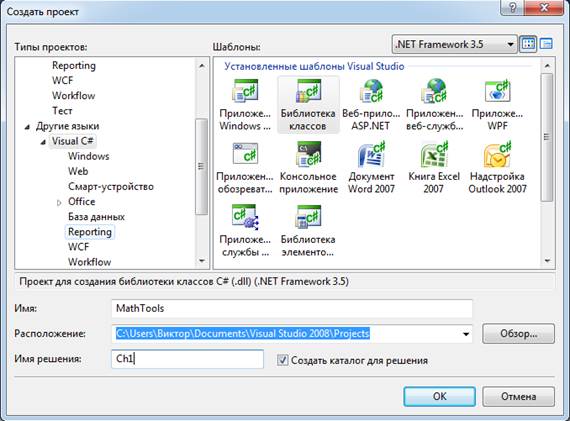
Рис. 4.1.2-2. Создание проекта DLL

В поле Имя (Name) задается имя строящейся DLL – MathTools в нашем случае.

В поле Расположение (Location) указывается путь к папке, где будет храниться Решение, содержащее проект.

В поле Solution выбран элемент CreateNewSolution, создающий новое Решение. Альтернативой является элемент списка, указывающий, что проект может быть добавлен к существующему Решению.

В окне Имя решения (Solution Name) задано имя Решения. Здесь зададим имя Ch1, все проекты этого примера будут вложены в одно Решение.

Необходимо обратить внимание и на другие установки, сделанные в этом окне - включен флажок (по умолчанию) Создать каталог для решений (Createdirectoryforsolution), в верхнем окошке из списка возможных каркасов выбран каркас Framework .Net 3.5. Задав требуемые установки и щелкнув по кнопке OK, получим автоматически построенную заготовку Проекта DLL, открытую в среде разработки проектов VS. На рис.4.1.2-3 показан внешний вид среды с построенным Решением и Проектом.

Среду разработки можно настраивать, открывая или закрывая те или иные окна, перемещая и располагая их по своему вкусу. Это делается стандартным способом, который рассмотрим далее.

В окне проектов Обозреватель решений (Solution Explorer) показано Решение с именем MathTools, содержащее проект DLL с именем MathTools. В папке Свойства (Properties) проект содержит файл с описанием сборки – ее имя и другие характеристики. В папке Ссылки (References) проект содержит ссылки на основные пространства имен библиотеки FCL, которые могут понадобиться в процессе работы DLL. Если содержимое этой папки не отображается, то необходимо щелкнуть по значку Показать все файлы в верхней части Обозревателя решений (Solution Explorer).

Поскольку всякая DLL содержит один или несколько классов, то для одного класса, которому по умолчанию дано имя Class1, заготовка построена. Класс этот, показанный в окне кода, пока что пуст – не содержит никаких элементов.

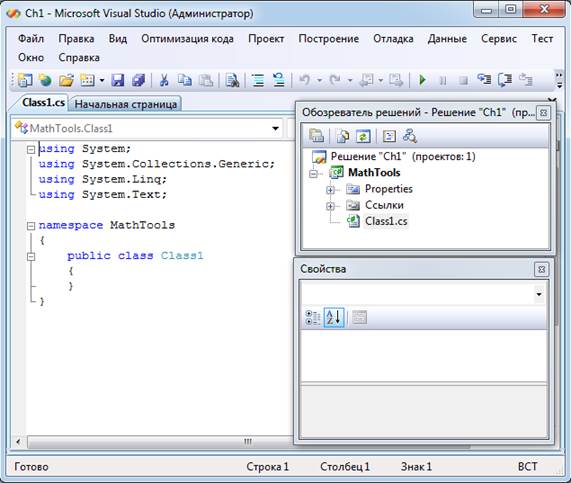
Рис. 4.1.2-3. Среда VS с начальным проектом DLL

Построенный автоматически класс вложен в пространство имен, которое по умолчанию получило имя, совпадающее с именем проекта – MathTools. Перед именем пространства заданы четыре предложения using, играющие роль инструкций для компилятора. В этих предложениях указываются имена пространств имен, присоединенных к проекту. Когда в коде создаваемого класса нужно сослаться на класс из пространств, указанных в предложениях using, можно задавать собственное имя этого класса, опуская имя пространства.

Итак,была рассмотрена подготовительная часть работы, которую выполнила VS. Дальше предстоит потрудиться самим. С чего следует начать? С переименования! Важное правило стиля программирования говорит, что имена классов должны быть содержательными. Изменим имя Class1 на имя MyMath. Как следует правильно изменять имена объектов в проектах? Никак не вручную. В окне кода проекта необходимо выделить имя изменяемого объектаClass1, затем в главном меню выбрать пункт Оптимизация кода(Refactor) и командуПереименовать(Rename). В открывшемся окне указать новое имяMyMath. Тогда будут показаны все места, требующие переименования объекта. В данном случае будет только одна очевидная замена, но в общем случае замен много, так что автоматическая замена всех вхождений крайне полезна.

Следующий шаг также продиктован правилом стиля – имя класса и имя файла, хранящего класс, должны совпадать. Переименование имени файлаClass1.cs на имя MyMath.cs делается непосредственно в окне проектов Обозреватель решений(SolutionExplorer).

Поскольку мы хотим создать аналог класса Math, то в нашем классе должны быть аналогичные методы. Начнем, как уже говорилось, с метода, позволяющего вычислить функцию sin(x). Заголовок метода сделаем такой же, как и в классе аналоге. В результате в тело класса добавим следующий код.

Осталось написать реализацию вычисления функции. Как и во всяком реальном программировании для этого требуется знание некоторых алгоритмов. Алгоритмы вычисления конечных и бесконечных сумм относятся к элементарным алгоритмам, изучаемым в самом начале программистских курсов. Несколько слов о том, как вычислять конечные и бесконечные суммы, аналогичные формуле, задающей вычисление функции sin(x).

Вычисление конечных сумм и произведений – это наиболее часто встречающийся тип элементарных задач, шаблон решения которых должен быть заучен, как 2*2. Какова бы не была сложность выражений, стоящих под знаком конечной суммы с заданным числом слагаемых, задачу всегда можно записать в виде:

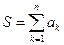
Покажем на примере формулы sin(x), как можно построить необходимые рекуррентные соотношения. Запишем соотношения для a₀, a_k, a_k+1:

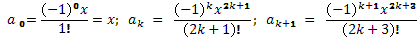
Вычислив отношение a_k+1/a_k, получим требуемое рекуррентное соотношение:

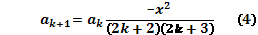
Значение a₀ задает базис вычислений, позволяя инициализировать начальное значение переменной a_k, а рекуррентное соотношение позволяет каждый раз в теле цикла вычислять новое значение этой переменной. Заметьте, введение рекуррентного соотношения позволило избавиться от вычисления факториалов и возведения в степень на каждом шаге цикла.

Иногда следует ввести несколько дополнительных переменных, хранящие вычисленные значения предыдущих членов суммы. Рекуррентная формула выражает новое значение a_k через предыдущее значение и дополнительные переменные, если они требуются. Начальные значения a_k и дополнительных переменных должны быть корректно установлены перед выполнением цикла в разделе Инициализация. В разделе Инициализация до цикла задаются начальные значения:первого слагаемого a_k=x, номер этого слагаемого k=0 и начальное значение суммы res=0. В цикле вначале выполняется прибавление a_k к сумме res, затем новое значение a_k вычисляется по рекуррентной формулеи увеличивается на единицу номер слагаемого k.

А теперь поговорим о том, как справляться с бесконечными суммами, примером которых является формула (1). Для математики бесконечность естественна. Множество целых чисел бесконечно, множество рациональных чисел бесконечно, множество вещественных чисел бесконечно. Элементы первых двух множеств можно пронумеровать – они задаются счетными множествами, множество вещественных чисел несчетно. Какой бы сколь угодно малый промежуток вещественной оси мы бы не взяли, там находится бесконечно много вещественных чисел. Число π и другие иррациональные числа задаются бесконечным числом цифр, не имеющим периода.

Мир компьютеров – это конечный мир, хотя в нем и присутствует стремление к бесконечности. Множества, с которыми приходится оперировать в мире компьютера, всегда конечны. Тип целых чисел в языках программирования – int – всегда задает конечное множество целых из некоторого фиксированного диапазона. В библиотеке FCLэто наглядно подтверждается самими именами целочисленных типов System.Int16, System.Int32, System.Int64. Типы вещественных чисел – double, float – задают конечные множества. Это достигается не только тем, что диапазон задания вещественных чисел ограничен, но и ограничением числа значащих цифр, задающих вещественное число. Поэтому для вещественных чисел компьютера всегда можно указать наборы таких двух чисел, между которыми нет никаких других чисел. Иррациональности компьютер не знает, – число π всегда задается конечным числом цифр.

Там, где в математике идет речь о пределах, бесконечных суммах, сходимости к бесконечности, в компьютерных вычислениях аналогичные задачи сводятся к вычислениям с заданной точностью – с точностью ε. Рассмотрим например задачу о вычислении предела числовой последовательности: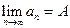

По определению число A является пределом числовой последовательности, если для любого сколь угодно малого числа ε существует такой номер N, зависящий от ε, что для всех n, больших N, числа a_n находятся в ε-окрестности числа A. Это определение дает основу для вычисления значения предела A. Понятно, что получить точное значение A во многих случаях принципиально невозможно, – его можно вычислить лишь с некоторой точностью и тоже не сколь угодно малой, поскольку существует понятие «машинного нуля» - минимального числа, все значения меньше которого воспринимаются как нуль. Когда два соседних члена последовательности – a_n и a_n+1 – начинают отличаться на величину по модулю меньшую чем δ, то можно полагать, что оба члена последовательности попали в ε-окрестность числа A и a_n+1 можно принять за приближенное значение числа A. Это рассуждение верно только при условии, что последовательность действительно имеет предел. В противном случае этот прием может привести к ошибочным выводам. Например, рассмотрим последовательность, элементы которой равны 1, если индекс элемента делится на 3, и равны 2, если индекс не делится на 3. Очевидно, что у этой последовательности предела нет, хотя существуют полностью совпадающие соседние члены последовательности.

При вычислении на компьютере значения функции, заданной разложением в бесконечный сходящийся ряд, не ставится задача получения абсолютно точного результата. Достаточно вычислить значение функции с заданной точностью ε. На практике вычисления продолжаются до тех пор, пока текущий член суммы не станет по модулю меньше заданного ε. Чтобы этот прием корректно работал, необходима сходимость ряда.

Вернемся к задаче вычисления функции sin(x) и приведем полный код проекта DLL, построенный на данный момент:

Поставленная цель достигнута, - построена DLL, содержащая класс, метод которого позволяет вычислять по заданному аргументу x функцию sin(x). Метод построен в полном соответствии с описанным алгоритмом. При его построении использованы две важные оптимизации. Во-первых, применено рекуррентное соотношение, позволяющее существенно ускорить время и точность вычисления функции. Во-вторых, аргумент x приведен к сравнительно небольшому интервалу, что увеличивает скорость сходимости и гарантирует работоспособность метода для больших значений x. Если не делать этой оптимизации, то для больших по модулю значений метод может давать некорректные результаты.

Построим Решение, содержащее проект, для чего в Главном меню среды выберем главный элемент Построение(Build), а затем выполним командуПостроитьMathTools (BuildSolution). В результате успешной компиляции будет построен файл с расширениемdll. Поскольку построенная сборка не содержит выполняемого файла, то непосредственно запустить наш проект на выполнение не удастся. Построим консольный проект, к которому присоединим построеннуюбиблиотеку DLL, и протестируем, насколько корректно работают созданные нами методы. Заодно разберемся с тем, как строится консольный проект и как к нему подсоединяется сборка, содержащая DLL.