Категория времени принадлежит к числу тех, которые играют ключевую роль не только в философии, математике, астрономии, но и в гуманитарных и исторических науках. Ни одна сфера человеческой деятельности не обходится без соприкосновения с реальностью времени: все, что движется, изменяется, живет, действует и мыслит, — все это в той или иной форме связано со временем. Однако удивительным образом само понятие времени представляет большие трудности для всякого, кто пытается постигнуть его природу. Не случайно о времени написаны горы литературы, особенно в последнее столетие, но число неразрешимых вопросов, как кажется, не только не уменьшается, а с каждым десятилетием, пожалуй, только возрастает.

В данной работе будут предприняты попытки рассмотреть лишь некоторые аспекты проблемы времени. Время непрерывно или, как некоторые полагают, дискретно. Поэтому для понимания его необходимо разобраться в природе континуума. В своей работе, посвященной анализу математического континуума, Георг Кантор подчеркивал, что невозможно определить континуум, если исходить из представлений о времени или пространстве. Потому что сами эти представления могут быть объяснены только с помощью понятия континуума, которое должно быть исходным и простым и не должно зависеть в своем содержании от других понятий. Это утверждение Кантора связано с его пониманием теории множеств как общего фундамента и математики в целом, и теории континуума в особенности.

Надо сказать, что размышления о природе времени с первых шагов научной и философской мысли в Древней Греции были неразрывно связаны с попытками решить проблему континуума. Ведь время, так же как и пространство, и движение представляет собой континуум, который можно мыслить либо как состоящий из неделимых частиц, либо как бесконечно делимую, то есть в непрерывную величину. Вот что пишет в этой связи Герман Вейль, чьи работы по философии математики относятся к классическим: «Издавна противостоят друг другу атомистическая концепция, согласно которой континуум состоит из отдельных точек, и противоположная точка зрения, считающая невозможным понять таким образом непрерывное течение. Первая концепция дает построенную логически систему неподвижно сущих элементов, но она не в состоянии объяснить движение и действие; всякое изменение сводится для нее к иллюзии. Второй же концепции не удалось ни во времена античного мира, ни позже, вплоть до Галилея, вырваться из сферы туманной интуиции, чтобы проникнуть в область абстрактных понятий, необходимых для рационального анализа действительности. Достигнутое в конце концов решение — это то, математически-систематическим образцом которого служит дифференциальное и интегральное исчисление. Но современная критика анализа снова разрушает изнутри это решение, хотя, правда, она и не дает себе ясного отчета во всем значении старой философской проблемы и приходит в итоге к хаосу и бессмыслице».

При обсуждении вопроса о природе континуума и особенно о природе времени как одномерного и необратимого континуума это сопоставление бытия и становления играет важную роль. Что касается времени, то тут ситуация особенно наглядна: те, кто считают предметом науки бытие как начало устойчивости и постоянства, а потому ищут неизменную основу изменчивых явлений, склонны устранять фактор времени при изучении природы. Напротив, те, кто приравнивает понятия природы и становления и пытаются создать средства для познания самого изменения и движения, убеждены в том, что время есть ключевой фактор в жизни природы и соответственно играет ведущую роль в ее познании.

Джордж Уитроу, автор обстоятельного исследования «Естественная философия времени», связывает эти два подхода к изучению природы с именами Архимеда и Аристотеля. Архимед, по его мнению, служит прообразом тех, чья философия физики предполагает исключение времени, т. е. тех, кто полагает, что время не является особенностью сущностью вещей. С другой стороны, Аристотель служит предшественником тех, кто рассматривает время как фундаментальное понятие, поскольку он утверждал, что имеется реальное становление и что мир имеет в своей основе временную структуру. Действительно, Аристотель был одним из первых, кто подверг критике как учение элеатов о неизменном и неподвижном бытии, по отношению к которому всякое становление есть только иллюзия, так и платоновское учение об идеях как потусторонних чувственному миру вневременных неизменных образах чувственных вещей. С точки зрения Платона, строгое научное знание можно получить лишь с помощью умозрения, ибо лишь ум в состоянии созерцать вечные идеи, недоступные чувствам; их он называет истинно сущим, противопоставляя всему становящемуся, не обладающему подлинным бытием. В отличие от Платона Аристотель стремится создать науку также и о движущемся и изменяющемся — о мире становления. По его замыслу, это должна быть наука о природе как начале движения и изменения — физика. И, как справедливо говорит Уитроу, Аристотель рассматривает время как фундаментальное понятие физики; не случайно его анализ времени и непрерывности не утратил своего значения по сегодняшний день.

Однако при этом у Аристотеля первостепенную роль играет и категория сущности как начала чего-то устойчивого и постоянного. Анализу именно этого начала посвящена «первая философия» Аристотеля — метафизика. Бытию уделяется и большое внимание в физике, поскольку и в изменчивом природном мире Аристотель пытается обнаружить некие инварианты — то прочное и устойчивое, что служит незыблемым фундаментом как самого природного сущего, так и науки о природе. Учение о субстанциях и вечном двигателе как высшей среди них как раз и составляет такой фундамент.

Необходимо отметить, что крайние формы противопоставления бытия и становления как взаимоисключающих реальностей в истории философии сравнительно редки, хотя они и выполняют важную эвристическую функцию в развитии теоретического знания. Так, в античности представителям Элейской школы — Пармениду и Зенону, доказывавшим реальность и познаваемость бытия и иллюзорность и непостижимость становления, впервые со всей остротой удалось поставить и обсуждаемую нами здесь проблему континуума. Другой крайний полюс — признание реальности только становления — представлен в древности Гераклитом, а в новейшее время — Бергсоном. Между этими полюсами располагается большинство мыслителей, пытающихся избежать крайних позиций и признающих как начало устойчивости и постоянства (сверхчувственное бытие), так и известные права на существование изменчивого и преходящего — становления.

Сегодня споры между приверженцами бытия и сторонниками становления ведутся в новой форме. При этом по-новому заостряется и вопрос о том, насколько существенным для познания природы, как и для самого ее существования, является фактор времени с характерной для него необратимостью. Об этом хорошо говорит В. С. Степин в своем фундаментальном исследовании «Теоретическое знание». Сравнивая принципиальную физики с другими науками, он указывает на различное отношение той и другой прежде всего к фактору времени. Классическая наука преимущественно уделяла внимание устойчивости, равновесию, однородности и порядку. В числе ее объектов были замкнутые системы. Как правило, это были простые объекты, знание законов развития которых позволяло, исходя из информации о состоянии системы в настоящем, однозначно предсказать ее будущее и восстановить прошлое. Для механической картины мира характерен был вневременной характер. Время было несущественным элементом, оно носило обратимый характер, т. е. состояния объектов в прошлом, настоящем и будущем были практически неразличимы. Иначе говоря, мир устроен просто и подчиняется обратимым во времени фундаментальным законам.

Иной подход обнаруживает современная физика, в частности синергетика, изучающая самоорганизующиеся сложные системы различной природы. При этом возникает вопрос о взаимоотношении неживой и живой природы, что ведет к изменению принципов классической и неклассической физики. Как отмечает В. С. Степин, в 20 веке появляется тенденция устранения разрывов между эволюционной теорией биологии и традиционным умозрением от эволюционных идей при строении физической картины мира. Синергетика имеет дело с открытыми системами, которые обмениваются энергией, веществом и информацией с окружающим миром. Состояния таких открытых систем становятся неустойчивыми, неравновесными. Процессы, происходящие в неравновесных системах, носят необратимый характер, и понятно, что необратимость времени получает в них решающую роль. Не случайно Илья Пригожин подчеркивает, что, в отличие от классической физики, синергетика возвращает все права становлению, в котором порядок возникает случайными отклонениями величин от их среднего значения.

Если классическая физика воспроизводит теорию Архимеда, исключающую «стрелу времени», т. е. рассматривает время как обратимое, то синергетика возвращается к Аристотелю, у которого время именно как необратимое играет основополагающую роль, становясь принципом становления, возведенного в ранг абсолютной реальности. Аристотель не признает никакого бытия как вневременной и неизменной реальности, для него нет ничего, кроме текучей изменчивости.

Теперь обратимся к понятию континуума. Можно утверждать, что формулировка этого понятия определяется тем фактом, что тот или иной ученый  решает проблему бытия и становления. Разумеется, каждый из ученых решает эту задачу по-своему, создавая свою систему понятий, и по-разному ставит проблему континуума.

Необходимо отметить еще один важный аспект рассматриваемой проблемы, которого до сих пор не касались: этот аспект связан с понятием бесконечности и с различением актуальной и потенциальной бесконечностей — различением, с древности и по сегодняшний день определяющим понимание как природы непрерывного вообще, так и сущности времени в частности.

Исторический анализ позволяет по-новому увидеть и глубже понять смысл современных дискуссий, посвященных проблеме континуума и различных его видов. В данной работе будут затронуты лишь наиболее важные, узловые моменты в истории понятия непрерывности, начиная с античности и кончая 17 – 18 веков. Как уже упоминалось, впервые проблема континуума была поставлена Зеноном из Элеи, выявившим парадоксы, возникающие при попытке мыслить движение в понятиях. Кратко содержание этих парадоксов передает Аристотель. Он говорит, что есть три основных рассуждения Зенона о движении, доставляющие большие затруднения тем, которые хотят их разрешить. Первое заключено в том, что не существует движения на том основании, что перемещающееся тело должно прежде дойти до половины, чем до конца. Второе, так называемый Ахиллес. Оно заключается в том, что существо более медленное в беге никогда не будет настигнуто самым быстрым, ибо преследующему необходимо раньше прийти в то место, откуда уже двинулось убегающее, так что более медленное всегда имеет некоторое преимущество. Третье заключается в том, что летящая стрела стоит неподвижно. Оно вытекает из предположения, что время слагается из отдельных «теперь».

Первая апория — «Дихотомия» — доказывает невозможность движения, поскольку движущееся тело, прежде чем преодолеть определенное расстояние, должно сначала пройти его половину, а для этого — половину этой половины и т. д. до бесконечности. В самом деле, если пространственный континуум рассматривать как актуально данное бесконечное множество элементов, то движение в таком континууме невозможно мыслить, ибо занять бесконечное количество последовательных положений в ограниченное время невозможно: строго говоря, движение здесь не может даже начаться.

В основе апории «Ахиллес» — то же самое затруднение: пока Ахиллес преодолевает расстояние, отделяющее его от черепахи, последняя пройдет еще один отрезок пути и т. д. до бесконечности. Чтобы догнать ее, самый быстроногий бегун должен последовательно занять бесконечное множество мест, которые занимала черепаха. В обеих апориях Зенон предполагает континуум делимым до бесконечности, но эту бесконечность считает актуально существующей, т. е. бытием в том смысле, о каком мы говорили выше.

В третьей апории «Стрела» философ доказывает, что летящая стрела покоится. Зенон здесь исходит из понимания времени как суммы неделимых моментов «теперь», а пространства — как суммы неделимых точек. В каждый момент времени, рассуждает Зенон, стрела занимает место, равное своему объему, а значит, движение можно мыслить лишь как сумму состояний покоя, потому что при действительном движении предмет должен занимать место большее, чем он сам. Атомистический континуум, как доказывает Зенон, не позволяет движению ни существовать, ни быть мыслимым.

 С помощью этих апорий Зенон пытается доказать, что, независимо от того, рассматривать ли континуум как делимый до бесконечности или же как состоящий из неделимых моментов, движение в равной мере окажется невозможным. Смысл парадоксов Зенона — в стремлении доказать, что множественный и изменчивый чувственный мир становления есть мир иллюзорный и не допускающий строго научного познания; об этом, как хочет доказать Зенон, неопровержимо свидетельствует то, что любая попытка постигнуть движение с помощью строгого рассуждения ведет к неразрешимым противоречиям...

Теория континуума Аристотеля служит фундаментом не только физики, но и математики, поскольку Аристотель предложил новое обоснование математики по сравнению с тем, какое давала пифагорейско-платоновская школа. Анализируя понятие непрерывности, как его обосновал Аристотель, можно видеть, как он понимает связь физики с математикой. Итак, что же такое непрерывность? Это есть, по Аристотелю, определенный тип связи элементов системы, отличающихся от других типов связи — последовательности и смежности. Последовательность, или следование по порядку, — условие смежности, а смежность — условие непрерывности. Важно уяснить различие между смежным и непрерывным: если предметы соприкасаются, но при этом сохраняют каждый свои края, так что соприкасающиеся границы не сливаются в одну общую, то мы имеем дело со смежностью. Если граница двух предметов оказывается общей, то тут речь идет о непрерывности. Непрерывными, по Аристотелю, могут быть не только части пространства и времени, но и движения; более того, подлинно непрерывным он считает то, что непрерывно по движению. Чтобы движение было непрерывным, должны быть выполнены три условия: единство вида движения, единство движущегося предмета и единство времени. Непрерывным называется то, что делится на части, всегда делимые. А это значит, что непрерывное не может быть составлено из неделимых частей. Таким образом, Аристотель снимает те трудности, которые возникают в физике при допущении, что пространство и время состоят из неделимых, и получает возможность мыслить движение как непрерывный процесс, а не как сумму «продвинутостей». Непрерывность составляет условие возможности движения и его мыслимости. Остаются, однако, две первых апории — «Дихотомия» и «Ахиллес», основанные на бесконечной делимости пространства и времени. Здесь для разрешения противоречия Аристотель действует иначе. Если любой отрезок пути в силу его непрерывности делим до бесконечности, то движение окажется невозможным только при забвении того, что и время, в течение которого тело проходит этот путь, тоже непрерывно, т. е. делимо до бесконечности. А если учесть, что непрерывности пути соответствует непрерывность времени, то парадокс снимается. Поэтому ошибочно рассуждение Зенона, что невозможно пройти бесконечное, т. е. коснуться бесконечного множества отдельных частей в ограниченное время. Ведь длина и время, как и вообще все непрерывное, называются бесконечными в двояком смысле: или в отношении деления, или в отношении границ. И вот, бесконечного в количественном отношении нельзя коснуться в ограниченное время, бесконечного согласно делению — возможно, так как само время в этом смысле бесконечно. Следовательно, приходится проходить бесконечность в бесконечное, а не в ограниченное время и касаться бесконечного множества частей бесконечным, а не ограниченным множеством

Определение непрерывности Аристотеля по существу совпадает с аксиомой Евдокса, получившей название также аксиомы Архимеда и сформулированной Евклидом в четвертом определении. У книги «Начал»: “Говорят, что величины имеют отношение между собой, если они, взятые кратно, могут превзойти друг друга”. Вот как Аристотель формулирует евдоксов принцип отношений, показывая, что его альтернативой будет парадокс «Дихотомия»: «Если, взявши от конечной величины определенную часть, снова взять ее в той же пропорции, т. е. не ту же самую величину, которая взята от целого, то конечную величину нельзя пройти до конца. Если же настолько увеличивать пропорцию, чтобы брать всегда одну и ту же величину, то пройти можно, так как конечную величину всегда можно исчерпать любой определенной величиной». Вероятно, теория отношений Евдокса была попыткой решить вопрос о возможности установления отношения также и несоизмеримых величин. Пока не была открыта несоизмеримость, отношения могли выражаться целыми числами, и для определения отношения двух величин нужно было меньшую взять столько раз, сколько необходимо для того, чтобы она сравнялась с большей. Но отношения несоизмеримых величин невозможно выразить в виде пропорции, члены которой будут целыми числами. 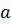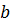Чтобы все же иметь возможность устанавливать отношения несоизмеримых величин, Евдокс предложил такой выход: если для двух величин и , где 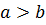, можно подобрать такое число 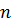, чтобы меньшая величина, взятая 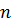раз, превзошла большую, т. е. чтобы было справедливо неравенство 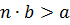, то величины 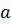и 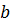 находятся между собой в некотором отношении. В противном же случае они не находятся ни в каком отношении, что действительно имеет место там, где приходится иметь дело с бесконечно малыми величинами, которые были известны грекам в виде, например, роговидных углов: последние не имеют отношения с прямолинейными углами, ибо роговидный угол всегда меньше любого прямолинейного угла. Как пишет И. Г. Башмакова, роговидные углы по отношению к любому прямолинейному являются актуальными бесконечно малыми, или неархимедовыми величинами. Именно эти величины, согласно Евдоксу, Архимеду и Аристотелю, не находятся ни в каком отношении с конечными.

Аристотель, как известно, не принимает понятия актуальной бесконечности, и его позиция совпадает с принципами античной математики. Он пользуется только понятием потенциально бесконечного, т. е. бесконечного делимого, которое, будучи проходимым по природе, не имеет конца прохождения, или предела.

Сказать, что бесконечное существует только как потенциальное, а не как актуальное — значит сказать, что оно становится, возникает, а не есть нечто законченное, завершенное, не есть бытие. Пример потенциально бесконечного — это беспредельно возрастающий числовой ряд, ряд натуральных чисел, который, сколько бы мы его ни увеличивали, остается конечной величиной. Потенциально бесконечное всегда имеет дело с конечностью и есть беспредельное движение по конечному. Принцип непрерывности, как его задал Аристотель, базируется на понятии потенциально бесконечного.

Бесконечное, таким образом, по Аристотелю, возможное, а не действительное, материя, а не форма: не случайно же материю Аристотель понимает как возможность. Не допуская актуальной бесконечности, Аристотель определяет бесконечное как то, вне чего еще всегда что-то есть. А может ли существовать нечто такое, вне чего больше ничего нет? И если да, то как его назвать? Бесконечное — это материя, т. е. в ее аристотелевском понимании нечто вполне неопределенное, не имеющее в себе своей связи и лишенное всякой структуры. Целое - это материя оформленная, и конец, граница, структурирующая его и делающая чем-то актуально сущим, действительным - это форма. Именно потому, что началом актуально сущего является форма, а форма есть предел, начало цели отвергает возможность актуально бесконечного: такое понятие является, по Аристотелю, как, впрочем, и по Платону, противоречит само себе.

Заключение

В данной работе были раскрыты некоторые аспекты и затруднения, связанные с апориями Зенона Элейского. Также эти апории были интерпретированы  с точки зрения современной математики. Как было видно в рассуждениях, все трудности и парадоксы возникали из-за недопонимания понятий и недостаточного количества математических и физических знаний.

Многие ученые на протяжении двух тысяч лет пытались разрешить эти загадочные апории, но большинство парадоксов так и остались неразгаданными и по сей день.

Возможно, спустя некоторое время, наши знания в области математического анализа и других отраслей математики станут еще больше. Некоторые понятия будут дополнены и станут еще более развернутыми и широкими. И вот тогда будет возможно окончательно разрешить все эти парадоксы. Как мне кажется, апории Зенона на протяжении всего времени являются самыми популярными среди ученых, несмотря на многообразие других различных парадоксов. Поэтому интерес к ним не пропадет до тех пор, пока их не решат. Остается только лишь наблюдать за поисками этих решений.

Список использованной литературы

1. Кудрявцев Л. В. – Курс математического анализа (в двух томах): Учебник для студентов университетов и вузов. – М.: Высш. школа, 1981, т. I. – 687 с., ил.

2. Грюнбаум А. – Философские проблемы пространства и времени. - М., 1969. С. 405.

3. Уитроу Дж. - Естественная философия времени. - М., 1964. С. 177.

4. Анисов А. М. - Апории Зенона и проблема движения // Труды научно-исследовательского семинара Логического центра Института философии РАН / РАН. Институт философии, Обществ. институт логики, когнитологии и развития личности. — М., 2000. — Вып. 14 / Редкол.: А. С. Карпенко (отв. ред.) и др. — Стр. 139—153.

5. Вейль Г. - О философии математики. - М.-Л., 1934. С. 102.

6. Кантор Г. - Основы общего учения о многообразиях // Новые идеи в математике. - СПб., 1914., Вып. 6.

7. Юшкевич А. П. - Идеи обоснования математического анализа в XVIII в. // Историко-математические исследования. - Вып. XXX. М., 1986. С. 26.

8. http://www.proza.ru/2009/07/06/918

9. http://fb.ru/article/156622/aporiya---eto-aporii-zenona-filosofiya