Главная цель данной работы заключается в желании понять, на какие реальные сложности в анализе апорий указывал Зенон Элейский. Ведь он только указал на эти трудности, но не пытался их решить. Именно поэтому мы не можем говорить о присвоении элейскому философу современную постановку проблем движения. Кстати говоря, такая постановка в литературе философии далеко не единая. Нехватка математических знаний и отсутствие многих математических понятий привели к возникновению парадоксов.   Многие считают, что если мы дадим определения необходимым понятиям, то парадоксы сразу же исчезнут. На мой взгляд, это не совсем правильно, поэтому я не соглашусь с этим. Апории Зенона затрагивают основы понимания человека о мире. Чтобы разобраться в них необходимо выбрать определенную систему требований философии для объяснения реальности, а не только уточнить какие-либо понятия. Только лишь спустя большое количество времени, а именно в настоящий момент, имея полный объем знаний во многих областях науки, мы можем придти к решению представленных парадоксов, рассмотрев все необходимые нам понятия. На сегодняшний день наши знания определенно намного шире и точнее, чем почти две тысячи с половиной лет назад. И может быть завтра мы, возможно, сможем уйти далеко вперед.

Чтобы начать разбираться в трудностях представленных парадоксов для начала необходимо ввести основные понятия, которыми необходимо будет руководствоваться в дальнейших рассуждениях.

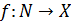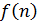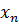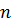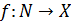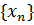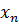Определение 1. Пусть X – какое либо множество и N – множество натуральных чисел. Всякое отображение  называется последовательностью элементов множества X. Элемент  обозначается через  и называется -м членом последовательности , а сама эта последовательность обозначается через  или , n=1, 2, … .

Каждый элемент 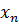 последовательности  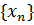представляет собой упорядоченную пару, состоящую из числа  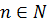и соответствующего ему при отображении  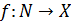элемента x множества X, т.е. 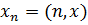. Второй элемент этой пары называется значением элемента последовательности 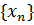, а первый – его номером.

Множество элементов последовательности всегда бесконечно. Два различных элемента последовательности могут иметь одно и то же значение, но заведомо отличаются номерами, которых бесконечное множество.

Множество значений элементов последовательности может быть конечным. Например, если всем 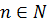 поставлен в соответствие один и тот же элемент 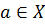, т.е. при всех  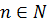имеет место 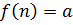, то множество значений последовательности 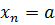, n=1, 2, … , состоит из одного элемента 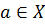. Такие последовательности называются стационарными.

 Если 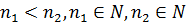, то член  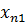последовательности  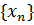называется членом, предшествующим члену 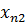, а член  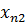членом, следующим за членом 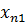. В этом смысле члены последовательности всегда упорядочены.

Очевидно, что числовая последовательность является частным случаем функции. Именно, последовательность является функцией, определенной на множестве натуральных чисел и принимающей значения в множестве действительных чисел, т.е. функцией вида: .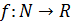

Иногда в качестве номеров удобно употреблять не все натуральные числа, а лишь некоторые из них. Например, натуральные числа, начиная с некоторого натурального числа 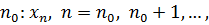 или одни четные числа: 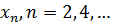. Случается, что для нумерации употребляются не только натуральные, но и другие числа, например, 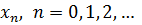(здесь в качестве еще одного номера добавлен нуль). Во всех этих случаях можно пронумеровать заново 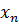, используя все натуральные числа m и только их. В первом примере следует положить 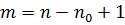, во втором –  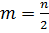, в третьем - 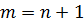. Поэтому в подобных случаях также говориться, что  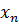образуют последовательность и, конечно, указывается, какие значения принимают номера n.

Так, например, последовательностью является прогрессия. На данный момент меня интересует бесконечно убывающая геометрическая прогрессия.

Определение 2. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число, т.е. геометрическая прогрессия – это числовая последовательность, заданная соотношениями:

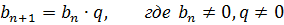
q – знаменатель прогрессии, определяющийся по формуле  .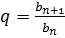

Если знаменатель геометрической прогрессии 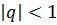, то каждый следующий член прогрессии по модулю меньше предыдущего. Если в этой прогрессии бесконечное число членов, то при 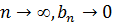. Такая последовательность называется бесконечно убывающей геометрической прогрессией.

Далее разберемся в понятии предела последовательности.

Определение 3. Число x называется пределом данной последовательности 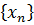, если для любого  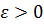существует такой номер , что для всех номеров 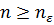 выполняется неравенство

.

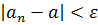При этом пишут .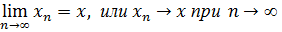

Употребляя логические символы, это определение можно записать в виде:

.

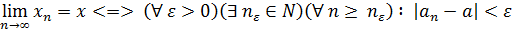Последовательность, у которой существует предел, называется сходящейся. Таким образом, последовательность 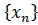 является сходящейся, если существует такое число x, что для любого  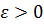найдется такой номер , что для всех 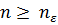 выполняется неравенство .

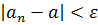Определение 4. Последовательность 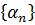 называется бесконечно малой последовательностью, если .

Примерами таких последовательностей могут быть, например последовательности  .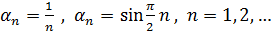

Отметим несколько свойств бесконечно малых последовательностей:

1. Алгебраическая сумма конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

2. Произведение бесконечно малой последовательности на ограниченную последовательность является бесконечно малой последовательностью.

Следствие. Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.

Теперь я могу начать рассматривать возникшие затруднения в апориях Зенона при рассмотрении апории «Ахиллес и черепаха».

 Ахиллес - всеми известный древнегреческий герой. Черепаха - самое медленное животное на земле. Но несмотря на эти факты, Зенон утверждал, что если провести соревнования по бегу между Ахиллесом и черепахой, то молодой спортсмен, как это не выглядит странным, никогда не догонит это медлительное животное. Зададим условия: пусть между Ахиллесом и финишем расстояние, равное единице, а расстояние от черепахи до финиша равно половине единице, т.е. . Пусть Ахиллес и черепаха начнут движение в одинаковый момент времени. Предположим, для определенности, что скорость Ахиллеса вдвое быстрее скорости черепахи. Тогда, после того как он пробежит  расстояния, наш герой заметит, что черепаха уже смогла за тот же промежуток времени преодолеть расстояние, равное  и все так же продолжает движение впереди Ахиллеса. Так, ситуация продолжается: пробежав  часть заданного пути, он заметит свою соперницу, обогнавшую его на  и так бесконечно. Значит, каждый раз, когда Ахиллес пробегает расстояние, отделяющее его от черепахи, та уже преуспела «убежать»  и все также остается впереди. Следовательно, делаем вывод, что Ахиллес никогда не сможет догнать черепаху. Иными словами можно сказать, что движение, которое уже начато, нельзя завершить.

Знатоки математического анализа всегда указывают на тот факт, что ряд будет сходиться к единице:

Определение 5. Числовым рядом называют сумму числовой последовательности вида  .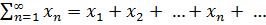

В данном случае мы имеем дело с бесконечно убывающей геометрической прогрессии с  :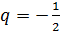

 .

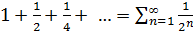Определение 6. Частичной суммой числового ряда называется сумма вида 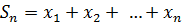 , где n – некоторое натуральное число.

Определение 7. Числовой ряд 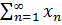 называется сходящимся, если существует конечный предел последовательности частичных сумм  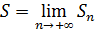. Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд  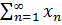называется расходящимся.

 Видно, собственно то, что Ахиллес пройдет установленный путь за конечный промежуток времени и, бесспорно, сможет обогнать черепаху. Как уже было замечено в 1 главе, есть противоречие, которое сумели увидеть Д. Гильберт и П. Бернайс. Они говорили о том, что такой парадокс довольно-таки часто пытаются обойти такими рассуждениями о том, что сумма бесконечного числа полученных интервалов времени все-таки сходится, а значит, получим конечный промежуток времени. Однако такое рассуждение вовсе не упоминает один немаловажный противоречивый момент, а именно парадокс, который основывается на том факте, что некоторая бесконечная последовательность событий, следующих поочередно друг за другом, представляет собой последовательность, завершенность которой мы не сможем себе представить, все же должна быть завершена.

Такая имеющая принципиальное значение невозможность завершения данной последовательности проявляется в том, что в ней нет последнего элемента. С каждым разом, указывая очередной член данной нам последовательности, можно показать член, который следует за ним.

Давайте предположим, что какая-то вычислительная машина, сможет реализовать 1-ую операцию за половину минуты, т.е. за  часть заданного времени. Следующее действие она выполнит за четверть минуты, т.е. за  часть времени. Еще одну следующую такая чудо-машина преодолеет за часть минуты и так  до бесконечности. Если подумать, то выходит, что данная машина для вычислений смогла бы уже под конец заданного времени, а именно первой минуты посчитать весь числовой ряд, состоящий только из натуральных чисел. На мой взгляд, понятно, что работы над производством этой вычислительной машины понесет за собой провал. Возникает вопрос: почему объект, который вышел из начала отрезка 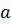, достигнет его конца в точке 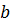, когда просчитает счетное множество точек  ?

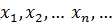В Древней Греции и вообще невозможно было представить бесконечную последовательность, которую можно было бы завершить. Поэтому автор всех этих апорий пришел к тому, что движение, из-за того, что необходимо посчитать все бесконечные точки, так и не прекратится. Почти на таких же доводах строится основание апории о том, что невозможно начать движение – апории «Дихотомия».

Размышления в этой апории достаточно легкое. Для преодоления всего пути, тело, которое начало движение для начала должно преодолеть  данного пути, но для преодоления этой  части, нужно пройти  этого пути и так продолжать бесконечно. Другими словами, при этих же условиях,  которые встречаются в предыдущем случае, мы получаем следующий перевернутый ряд точек:

,

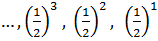
Если в апории «Ахиллес и черепаха» в соответствующем ряду не было крайней точки, то в « Дихотомии» в таком ряду нет первоначальной точки. Из этого следует утверждение Зенона о том, что движение не может быть начато. А если движение невозможно закончить и невозможно начать, то получается, что движения не существует в принципе.

Согласно одной легенде, кто-то из древних мыслителей посмел выразить противоречие Элейскому философу. На что тот приказал побить беднягу: он вовсе не хотел отвергать чувственное восприятие движения. Мудрец говорил о том, что движение немыслимо и что такое требователное размышление о движении приведет к серьезным разногласиям, которые невозможно будет разрешить. Следовательно, если надо покончить с апориями, то для этого нужно больше ссылаться на теоретические доказательства, а не опираться на чувства. Необходимо проанализировать одно интересное возражение, которое обосновано теорией, и которое выставили против апории «Ахиллес и черепаха».

Предположим, что Ахиллес начал движение в одном направлении вместе с двумя черепахами. Тогда 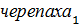 находится ближе к Ахиллесу, в отличие от 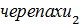. Чтобы представить, что Ахиллес не сможет справиться со своей задачей  обогнать 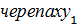, буду вести рассуждение таким образом. За тот промежуток времени, за который Ахиллес должен пробежать расстояние, которое разделяет их в самом начале,  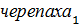сумеет проползти вперед некоторое расстояние. Пока Ахиллес начнет проходить следующее расстояние, 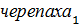снова пройдет далее. Такое прохождение определенного расстояния повторяется бесконечно много раз. Ахиллес с каждым разом будет приближаться к 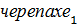, но ему так и не удастся «победить» черепаху. Получается противоречие.

Пусть тогда Ахиллес будет пытаться догонять наиболее дальнюю от спортсмена 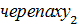. Это же построение рассуждения позволит убедиться, что Ахиллес сможет достаточно близко приблизиться к 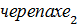, но одержать «победу» над  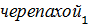он все-таки не сможет. Вот и приходим к логическому противоречию.

В данной ситуации трудно возразить что-то против. Нужно выявить формальную суть дела, что разрешит от дискуссии перейти к строгим рассуждениям. По моему мнению, эту апорию можно привести к таким утверждениям:

1. Тело, проходящее от 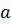 к 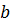  должно пройти через все точки отрезка 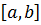, независимо от того каким он будет.

2. Абсолютно любой интервал 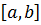 возможно записать в виде последовательности бесконечно убывающих отрезков …

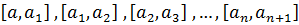3. Так как бесконечная последовательность не содержит последнюю точку, то движение не может быть завершено.

Пояснить этот вывод можно различными способами. Наиболее простой пример – «Самое быстрое никогда не сможет догнать самое медленное» - уже был рассмотрен. Можно сделать наиболее действенную иллюстрацию, из которой можно увидеть, что Ахиллес, который вышел из точки 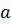, безо всякого успеха пытается догнать черепаху, находящуюся в точке 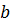. Из этого предположения сама апория не изменяется. Тогда примером будет служить более точное утверждение - «Самое быстрое никогда не сможет догнать неподвижное». 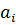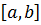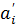Однако, никто не говорит, что последовательности отрезков , которые убывают на всем промежутке, для  и  для 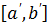 обязаны быть одинаковыми. А вот если эти отрезк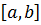и  и 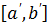 будут отличными друг от друга, то тогда их разбиения на бесконечные последовательности убывающих отрезков будут разными. В этой идее Ахиллеса и двух имеющихся черепах -  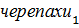и 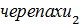 - разделяют отличные друг от друга расстояния. Из этого получается два разных отрезка с одной общей точко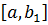й -  и 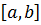. Отличающиеся друг от друга отрезк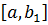и  и 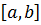тянут за собой разные бесконечные последовательности точек, и нельзя использовать одну точку вместо другой. Впрочем, именно такая неправильная операция используется в доводах о двух черепахах.

Если не смешивать иллюстрации и существо апории, то можно утверждать, на наш взгляд, что апории Ахилл и Дихотомия симметричны по отношению друг к другу. В самом деле, Дихотомия также водится к следующим трем утверждениям:

4. Тело, проходящее от 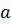 к 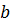должно пройти через все точки отрезка 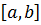, независимо от того каким он будет.

5. Абсолютно любой интервал 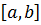 возможно записать в виде последовательности бесконечно убывающих отрезков .

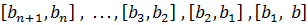6. Так как бесконечная последовательность 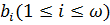не содержит первую точку, то движение не может быть начато.

Следовательно, апория «Ахиллес и черепаха» имеет обоснование на идее о невозможности завершения движения из-за того, что необходимо последовательно побывать в каждой точке полученного бесконечного ряда, который упорядочен в натуральных числах и не содержит последнего числа. В свою очередь апория « Дихотомия» говорит о том, что движение начать невозможно из-за того, что у  бесконечного ряда точек, который упорядочен в целых отрицательных числах не содержится первого числа.

Проведя тщательный анализ первых двух апорий, можно обнаружить, что и одна, и вторая допускают такое свойство пространства и времени, как непрерывность в смысле их бесконечной делимости. Такое предположение свойства непрерывности имеет отличие от современного подхода к данному вопросу. Без гипотезы о том, что всякий интервал пространства или времени мы можем поделить на небольшие интервалы, получается, что эти две апории разрушаются. Зенон осознавал это и поэтому привел в качестве аргумента тезис, который исходит из допустимости такого свойства пространства и времени, как дискретность, т. е. допустимость существования элементарных, неделимых длин и времен.

Из всего вышесказанного можно придти к выводу, что трудности апорий «Ахиллес и черепаха» и «Дихотомия»,  так до сих пор не смогли преодолеть.