Толщина и/или ширина многозатворных МОП транзисторов достигает значений менее 10 нанометров. При этих условиях электроны в канале (если мы в качестве примера берем n-канальный прибор) образуют или двухмерный электронный газ (2DEG), если мы рассматриваем двухзатворный прибор, или одномерный электронный газ (1DEG), если мы рассматриваем трех- или четырехзатворный МОП-транзистор. Рассмотрим двухзатворный прибор, выполненный в тонком слое кремния. Примем систему координат, используемую на рис.8.8, толщина слоя кремния составляет 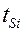, электроны свободно перемещаются в направлениях x и z, но они ограничены в направлении y. В тонком и узком трех- или четырехзатворном приборе электроны свободно двигаются только в направлении x и ограничены в направлениях y и z. Это приводит к образованию энергетических подзон и электронных распределений в слое кремния, которые могут значительно отличаться от тех, что описываются классической теорией. В частности, инверсионные слои не обязательно локализуются у поверхности кремниевого слоя, а могут образовываться в глубине слоя, увеличивая объем инверсии. Квантовые ограничения электронов являются также причиной ранее не наблюдавшихся до этого момента свойств подвижности и порогового напряжения.

    Объемная инверсия – это явление, появляющееся в очень тонком (или узком) слое многозатворных КНИ МОП-транзисторов, в результате которого инверсные носители локализованы не вблизи границы раздела Si/SiO₂, как предполагается классической теорией приборов, а в центре слоя. Чтобы корректно спрогнозировать объемную инверсию, необходимо решить уравнения Шредингера и Пуассона самосогласованным методом.

   Когда многозатворный МОП-транзистор работает в режиме объемной инверсии, электроны образуют низкоразмерный электронный газ (двухмерный электронный газ для двухзатворного прибора и одномерный электронный газ для трех-, П-, W-затворного приборов или прибора с окружающим затвором). В результате формируются энергетические подзоны. Примеры профилей концентрации электронов в двухзатворных МОП-транзисторах для различной толщины слоя кремния 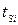 и для V_G > V_T  представлены на рис.8.14. Профили концентрации электронов в FinFET транзисторе, трехзатворном МОП транзисторе и транзисторе с окружающим затвором показаны на рис.8.15. В каждом случае наблюдается высокая концентрация электронов в середине слоя кремния или плавника, что соответствует объемной инверсии. Прямым следствием объемной инверсии является увеличение подвижности инверсных носителей в тонкопленочном приборе.

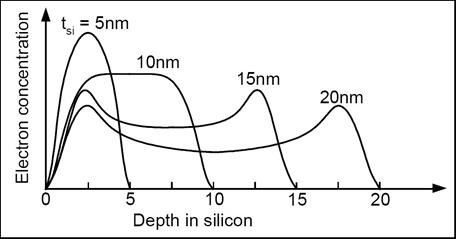
Рис. 8.14. Профиль распределения электронов в двухзатворных МОП-транзисторах с различными значениями толщины слоя кремния ( ).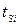

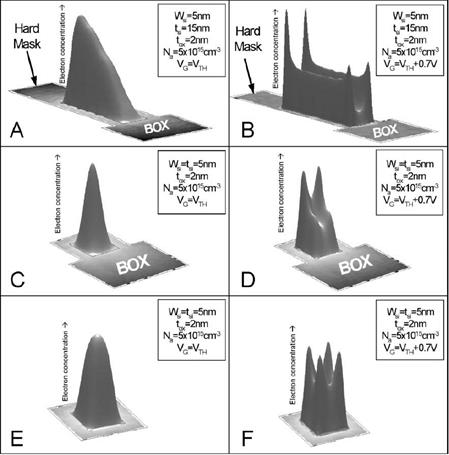
Рис. 8.15. Профиль распределения электронов в FinFET транзисторе (A,B), трехзатворном полевом транзисторе (C,D) и транзисторе с окружающим затвором (E,F) при пороговом напряжении (A,C,E) и напряжении выше порогового (B,D,F). Вертикальный масштаб (электронная концентрация) различается для каждого графика.

Эффекты подвижности

    Объемно-инверсные носители испытывают меньшее рассеяние на поверхности раздела, чем носители в поверхностном инверсном слое. В результате в двухзатворных транзисторах обеспечивается увеличение подвижности и крутизны. Зависимость подвижности от толщины слоя в двухзатворных МОП-транзисторах проиллюстрирована на рис.8.16. В толстых пленках нет взаимодействия между передним и задним каналом, и нет объемной инверсии. Подвижность идентична подвижности в объемном МОП-транзисторе. Если слой тоньше, появляется объемная инверсия, и подвижность увеличивается, так как уменьшается рассеяние на поверхности раздела Si-SiO₂.

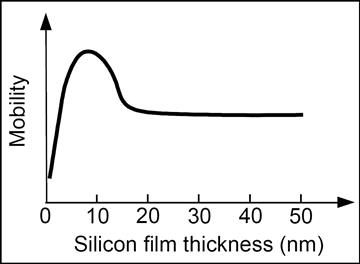
Рис. 8.16. Зависимость подвижности инверсных носителей от толщины слоя кремния в двухзатворном транзисторе.

В более толстых слоях инверсные носители концентрируются вблизи поверхности, а в более тонких слоях большинство носителей концентрируется около середины слоя кремния, отдаляясь от центров рассеяния на поверхности раздела (рис. 8.14), что увеличивает их подвижность. В очень тонких слоях кремния, однако, инверсные носители в области объемной инверсии испытывают поверхностное рассеяние по причине их физической близости к поверхностям раздела, и подвижность падает с уменьшением толщины слоя.

Пороговое напряжение

Классическая теория объясняет, что пороговое напряжение уменьшается в полностью обедненном КНИ МОП-транзисторе, когда уменьшается толщина слоя кремния, предполагая концентрацию примеси N_a постоянной, − сокращение толщины кремниевого слоя соответствует уменьшению заряда обеднения qN_at_Si. Когда толщина слоя становится ниже 10нм, обедненный заряд очень мал, и им обычно можно пренебречь. С другой стороны, учитываются две неклассические добавки к пороговому напряжению. Первая добавка исходит из факта, что концентрация инверсных носителей для достижения порогового напряжения должна быть больше, чем прогнозирует классическая теория. Таким образом, поверхностный потенциал Ф в тонком слое кремния больше 2Ф_F. Вторая добавка возникает из расщепления зоны проводимости на две подзоны: минимальная энергия подзон (и таким образом минимальная энергия зоны проводимости) увеличивается при уменьшении толщины слоя. Вторая добавка увеличивает напряжение на затворе, необходимое для достижения определенной концентрации инверсных носителей. Это также увеличивает пороговое напряжение.

Выражение для величины порогового напряжения с учетом вышеуказанных добавок получено в [9]:

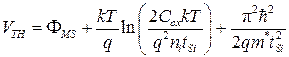                                    (8.18)

Первый член уравнения (8.18) – разница работ выхода затвор-кремний. Второй член уравнения представляет поверхностный потенциал Ф в канале. Он обратно пропорционален логарифму от толщины кремниевого слоя 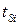. В очень тонких пленках Ф может быть значительно больше 2Ф_F, и как результат, концентрация инверсных носителей при пороге может быть больше в тонкослойном приборе, чем в более толстом транзисторе. Это увеличение порогового напряжения корректно предсказывается классической теорией, хотя она не включает уравнение Шредингера. Третий член уравнения (8.18) относится к изменению минимальной энергии в зоне проводимости, которое может быть предсказано только через квантомеханические вычисления (рис.8.17). Подобное увеличение порогового напряжения наблюдается в трехзатворном, П-затворном, Ω-затворном и GAA транзисторах, когда уменьшается  размер  кремниевого  плавника.

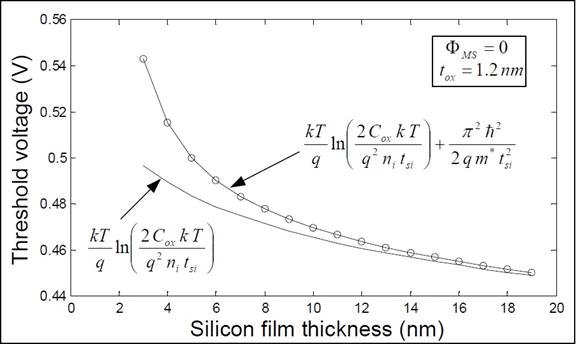
Рис. 8.17. Зависимость порогового напряжения от толщины слоя кремния в длинноканальном, слаболегированном/нелегированном двухзатворном транзисторе. Нижняя кривая представляет классическую часть уравнения (8.18), а верхняя кривая включает квантовомеханическое приближение.

Заключение

    Подавление короткоканальных эффектов и максимилизация тока в открытом состоянии, необходимые для продолжения масштабирования МОПТ в нанометровом диапазоне, совершаются за счет достижений в материалах (high-k диэлектрики, металлические затворы, металлические области стока и истока и др.), процессах (создание механических напряжений для повышение тока в открытом состоянии без увеличения тока в закрытом состоянии), схемных инновациях (таких как смещение подложки для увеличения масштабируемости и допущение динамической регулировки компромисса между характеристиками и потребляемой мощностью) и структурах (многозатворные МОПТ). Так как расстановка по важности требований к масштабированию МОПТ зависит от конкретных приложений, могут возникнуть расхождения в оптимальной конструкции структуры (например, для логических схем и схем памяти), так что будущие ИС могут одновременно содержать различные транзисторные структуры. Исходя из фундаментального предела масштабирования, определяемого туннельным током сток-исток, кремниевые МОПТ могут масштабироваться до длин затвора менее 10нм. Темп масштабирования в будущем может замедлиться, впрочем, в зависимости от того насколько профили примесей и размеры канала могут точно контролироваться/задаваться в рентабельном промышленном производстве. Альтернативные материалы для канала, такие как Ge и GaAs, менее масштабируемы и поэтому маловероятно, что могут сохранить улучшения характеристик МОПТ после того, как кремний достигнет предела. Так как для кремния фундаментальный предел подпорогового размаха характеристик S=60мВ/декаду, в дополнение к МОПТ потребуются альтернативные приборы с более крутой характеристикой включения, чтобы обеспечить ультранизкое потребление мощности для быстро растущего рынка потребителей мобильной электроники. У технологов и проектировщиков имеются большие возможности для инноваций, способных поддержать кремниевую революцию.

Литература:

1. Зебрев Г.И. Физические основы кремниевой наноэлектроники, М.: БИНОМ, 2011, с. 159-186.

2. Парменов Ю.А., Элементы твердотельной наноэлектроники. Учебное пособие. М.: МИЭТ, 2011, гл. 6.

3. FinFETs and Other Multi-Gate Transistors, Еd. Jean-Pierre Colinge, Springer Science+Business Media, LLC, 2008.

4. Sekigawa T. and Hayashi Y., Calculated threshold-voltage characteristics of an XMOS transistor having an additional bottom gate. Solid-State Electronics, v. 27, р.827 (1984).

5. Lim H.K. and Fossum J.G., Threshold voltage of thin-film silicon-on-insulator (SOI) MOSFETs IEEE. Trans. on Electron Devices v.30,№10, р.1244 (1983).

6. Yan, R.H, Ourmazd A. and K.F. Lee: Scaling the Si MOSFET: from bulk to SOI to bulk. IEEE Transactions on Electron Devices v.39, №7, р.1704 (1992).

7. Auth C.P., Plummer J.D, Scaling theory for cylindrical, fully-depleted, surrounding-gate MOSFET's. IEEE Electron Device Letters v,18, №2, р.74 (1997).

8. Wong H.S., White M.H., Krutsck T.J., Booth R.V., Modeling of transconductance degradation and threshold voltage in thin oxide MOSFETs. Solid-State Electronics, v.30, №9, р.953 (1987).

9. Poiroux T., Vinet M., Faynot O., Widiez J., Lolivier J., Ernst T., Previtali B., Deleonibus S., Multiple gate devices: advantages and challenges. Microelectronic Engineering v.80, р.378 (2005).

10. Skotnicki T., Hutchby J.A., Tsu-Jae King, Boeuf F. The end of CMOS scaling, IEEE Circuits and Devices Magazine, 2005, №1-2, pp.16-26.

11. Frank D.J., Dennard R.H., Nowak E. at al., Device Scaling Limits of Si MOSFETs and Their Application Dependencies, Proceedings of the IEEE, 2001, v.89, №3, pp.259-288.

12. Taur Y., Buchanan D.A., Wei Chen, Frank D.J. at al., CMOS Scaling into the Nanometer Regime, Proceedings of the IEEE, 2001, v.85, №4, pp.486-504.

13. Wong P., Frank D.J., Solomon P.M. at al., Nanoscale CMOS. Proceedings of the IEEE, 1999, v.87, №4, pp.537-570.

14. Haensch W., E. J. Nowak,R. H. Dennard,P. M. Solomon,A. Bryant,O. H.Dokumaci,A. Kumar,X. Wang,J. B. Johnson,M. V. Fischetti Silicon CMOS devices beyond scaling, IBM J. RES. & DEV. VOL. 50 NO. 4/5 JULY/SEPTEMBER 2006, pp.339-361.

15. Taur Y., CMOS design near the limit of scaling. IBM J. RES. & DEV. VOL. 46, NO. 2/3, 2002, pp.213-222.

16. Wong H.-S. P., Beyond the conventional transistor, IBM J. RES. & DEV. VOL. 46 NO. 2/3 MARCH/MAY 2002, pp. 133-168.

17. Bokor J., King T.-J., Hergenrother J., Bude J., Muller D., Skotnicki T., Monfray S. and Timp G., Advanced MOS-Devices, in «High Dielectric Constant Materials», Ed. H.R. Huff, D.C. Gilmer, Springer, 2005, pp.667-705.

18. Liu T.-J.K. and Chang L. Transistor Scaling to the Limit, in «Into the Nano Era: Moore’s Law Beyond Planar Silicon CMOS», Ed. H. R. Huff, Springer, 2009, pp.191-223.

19. Chang L., Choi Y.-K., Ha D. at al. Extremely Scaled Silicon Nano-CMOS Devices,Proceedings of the IEEE, 2003, v.91, №11, pp.1860-1873.

Задание для СРС

1.Изучить материал лекции №8 по конспекту и по литературным источникам.

Вопросы для самопроверки

1. Что такое электростатическое качество МОПТ?

2. За счет каких факторов уменьшается пороговое напряжение короткоканальных транзисторов?

3. Опишите структуры многозатворных КНИ МОПТ.

4. В чем заключаются преимущества многозатворных МОПТ?

5. Что определяет характерная длина МОПТ?

6. Что такое угловой эффект в структуре МОПТ?

7. Как подвижность носителей в канале двухзатворного МОПТ зависит от толщины слоя кремния?

8. Какие требования (перечисленные в порядке их важности), предъявляются к «совершенному» МОПТ?

[1] Обратите внимание, что характерная длина прибора уже встречалась в лекции 5 (формула (5.1.3)) при рассмотрении поля в области отсечки.