Если не возникает разночтений (например, когда все цифры представляются в виде уникальных письменных знаков), число 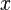записывают в виде последовательности его 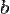-ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо^[1]:

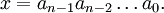
В ненулевых числах 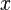левые нули обычно опускаются.
Во избежание путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса:

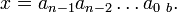
Построение такой записи числа называют позиционным кодированием числа, а саму запись — позиционным кодом числа.
Количество записываемых кодов такой записью определяется в комбинаторике и равно количеству размещений с повторениями:

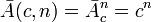, где

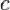— размерность множества из которого берутся цифры 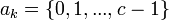( основание системы кодирования),
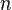— количество цифр 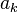в записи.
При 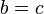и показательной весовой функции 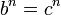, при этом образуются системы счисления с равномерным распределением чисел на числовой оси c расстояниями между соседними числами на числовой оси равными 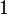. Из-за этих двух свойств такие системы счисления получили наибольшее распространение.

С помощью 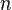позиций в 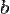-ричной системе счисления с 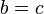можно записать целые числа в диапазоне от 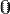до 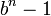( 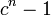), то есть всего 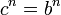различных чисел с расстояниями между соседними числами на числовой оси равными .

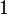Для записи чисел в системах счисления с основанием до 36 включительно в качестве цифр (знаков) используются арабские цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) и, затем, буквы латинского алфавита (a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z). При этом, a = 10, b = 11 и т. д., иногда x = 10.

При одновременной работе с несколькими системами счисления для их различения основание системы обычно указывается в виде нижнего индекса, который записывается в десятичной системе:

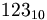— это число 123 в десятичной системе счисления;

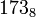— то же число в восьмеричной системе счисления;

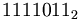— то же число, но в двоичной системе счисления;

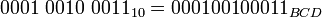— то же число, но в десятичной системе счисления с двоичным кодированием десятичных цифр (BCD);

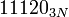— то же число, но в несимметричной троичной системе счисления;

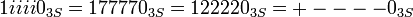— то же число, но в симметричной троичной системе счисления, знаки "i", "7", "2" и "-" обозначают "-1", знаки "1" и "+" обозначают "+1".

В некоторых специальных областях применяются особые правила указания основания. Например, в программировании шестнадцатеричная система обозначается:

в ассемблере и записях общего рода, не привязанных к конкретному языку, буквой h (от hexadecimal) в конце числа (синтаксис Intel);

в Паскале знаком «$» в начале числа;

в C и многих других языках комбинацией 0x или 0X (от hexadecimal) в начале.

В некоторых диалектах языка Си по аналогии с «0x» используется префикс «0b» для обозначения двоичных чисел. (Обозначение «0b» не входит в стандарт ANSI C.)

В русских счётах для записи чисел в десятичной показательной позиционной системе счисления применяется унарнодесятичная система записи (представления) десятичных цифр с одной избыточной унарнодесятичной цифрой «1111111111»= 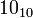на каждый разряд.

ПЕРЕВОД ЧИСЕЛ ИЗ ШЕСТНАДЦАТЕРИЧНОЙ СИСТЕМЫ В ДВОИЧНУЮ И ВОСЬМЕРИЧНУЮ

Алгоритм перевода чисел из шестнадцатеричной системы счисления двоичную крайне прост. Необходимо только заменить каждую цифру шестнадцатеричного числа ее эквивалентом в двоичной системе счисления (в случае положительных чисел). Как и в предыдущих параграфах, удобно и полезно воспользоваться таблицей соответствия, приведенной в Приложении. Отметим только, что каждое шестнадцатеричное число следует заменять двоичным, дополняя его до 4 разрядов (в сторону старших разрядов).

Арифметические операции

Производятся по тем же правилам, что и в десятичной с.ч.

если результат поразрядного сложения в каждом разряде меньше основания системы счисления, т.е.

аi + bi, < р,

то в соответствующий разряд суммы записывается цифра, которая отображает количество, равное ci = ai + bi

В том случае, если результат поразрядного сложения больше ос­нования системы счисления или равен ему, т.е.

аi + bi, ³ р, то в соответствующий разряд суммы записывается цифра, которая отображает количество, равное:

Ci = ai + bi - p

и в старший разряд c1+i переносится единица, которая должна учи­тываться при суммировании в этом разряде. При вычитании поступают по аналогичным правилам.

Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.

Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных.

Примеры.