Проверим зубья на выносливость по напряжениям изгиба по формуле 3.22 [1]:
sF = Ft · KF · YF / (b · mn) £ [sF]
Здесь коэффициент нагрузки KF = KFb · KFv (см. стр. 42 [1]). По таблице 3.7 [1] выбираем коэффициент расположения колес KFb = 1,089, по таблице 3.8 [1] выбираем коэффициент KFv=1,35. Таким образом коэффициент KF = 1,089 · 1,35 = 1,47. Y – коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа Zv (см. гл. 3, пояснения к формуле 3.25 [1]):
у шестерни: Zv1 = z1 / cos3 (b) = 43 / cos3 (0o) = 43
у колеса: Zv2 = z2 / cos3 (b) = 137 / cos3 (0o) = 137
Тогда: YF1 = 3,688; YF2 = 3,582
Допускаемые напряжения находим по формуле 3.24 [1]:
[sF] = soF lim b · KFL / [Sf].
KFL – коэффициент долговечности.
KFL = (NFO / NF) 1/6,
где NFO – базовое число циклов нагружения; для данных сталей NFO = 4000000;
NF = 60 · n · c · tS
Здесь:
– n – частота вращения, об./мин.; nшест. = 1465,502 об./мин.; nкол. = 465,239 об./мин.
– c = 1 – число колёс, находящихся в зацеплении;
tS = 20000 ч. – продолжительность работы передачи в расчётный срок службы.
Тогда:
NF (шест.) = 60 · 1465,502 · 1 · 20000 = 1758602400
NF (кол.) = 60 · 465,239 · 1 · 20000 = 558286800
В итоге получаем:
КFL (шест.) = (4000000 / 1758602400) 1/6 = 0,363
Так как КFL (шест.)<1.0, то принимаем КFL (шест.) = 1
КFL (кол.) = (4000000 / 558286800) 1/6 = 0,439
Так как КFL (шест.)<1.0, то принимаем КFL (шест.) = 1
Для шестерни: soF lim b = 414 МПа;
Для колеса: soF lim b = 360 МПа.
Коэффициент [SF] безопасности находим по формуле 3.24 [1]:
[SF] = [SF]' · [SF]».
где для шестерни [SF]' = 1,75;
[SF]' = 1;
[SF (шест.)] = 1,75 · 1 = 1,75
для колеса [SF]' = 1,75;
[SF]» = 1.
[SF (кол.)] = 1,75 · 1 = 1,75
Допускаемые напряжения:
для шестерни: [sF1] = 414 · 1 / 1,75 = 236,571 МПа;
для колеса: [sF2] = 360 · 1 / 1,75 = 205,714 МПа;
Находим отношения [sF] / YF:
для шестерни: [sF1] / YF1 = 236,571 / 3,688 = 64,146
для колеса: [sF2] / YF2 = 205,714 / 3,582 = 57,43
Дальнейший расчет будем вести для колеса, для которого найденное отношение меньше.
Проверяем прочность зуба колеса по формуле 3.25 [1]:
sF2 = (Ft · KF · YF1) / (b2 · mn) =
(1742,34 · 1,47 · · 3,582) / (36 · 2) = 127,422 МПа
sF2 = 127,422 МПа < [sf] = 205,714 МПа.
Условие прочности выполнено.
Механические характеристики материалов зубчатой передачи
| Элемент передачи | Марка стали | Термообработка | HB1ср | sв | [s] H | [s] F |
| HB2ср | H/мм2 | |||||
| Шестерня | 45 | улучшение | 230 | 780 | 481,818 | 236,571 |
| Колесо | 45 | улучшение | 200 | 690 | 427,273 | 205,714 |
Параметры зубчатой цилиндрической передачи, мм
| Проектный расчёт | |||||||
| Параметр | Значение | Параметр | Значение | ||||
| Межосевое расстояние aw | 180 | Угол наклона зубьев b, град | 0 | ||||
| Модуль зацепления m | 2 | Диаметр делительной окружности: | |||||
| Ширина зубчатого венца: |
| шестерни d1 колеса d2 | 86 274 | ||||
| шестерни b1 колеса b2 | 41 36 | ||||||
| Числа зубьев: |
| Диаметр окружности вершин: | |||||
| шестерни z1 колеса z2 | 43 137 | шестерни da1 колеса da2 | 90 278 | ||||
| Вид зубьев | прямозубая передача | Диаметр окружности впадин: | |||||
| шестерни df1 колеса df2 | 81 269 | ||||||
| Проверочный расчёт | |||||||
| Параметр | Допускаемые значения | Расчётные значения | Примечание | ||||
| Контактные напряжения sH, H/мм2 | 427,273 | 389,293 | - | ||||
| Напряжения изгиба, H/мм2 | sF1 | 236,571 | 115,193 | - | |||
| sF2 | 205,714 | 127,422 | - | ||||
Расчёт 2-й зубчатой цилиндрической передачи
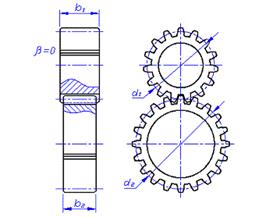
Проектный расчёт
Так как в задании нет особых требований в отношении габаритов передачи, выбираем материалы со средними механическими характеристиками (см. гл. 3, табл. 3.3 [1]):
– для шестерни: сталь: 40ХН
термическая обработка: улучшение
твердость: HB 280
– для колеса: сталь: 40ХН
термическая обработка: улучшение
твердость: HB 265
Допустимые контактные напряжения (формула (3.9) [1]), будут:
[sH] = sH lim b · KHL / [SH]
По таблице 3.2 гл. 3 [1] имеем для сталей с твердостью поверхностей зубьев менее HB 350:
sH lim b = 2 · HB + 70.
sH lim b (шестерня) = 2 · 280 + 70 = 630 МПа;
sH lim b (колесо) = 2 · 265 + 70 = 600 МПа;
[SH] – коэффициент безопасности [SH]=1,1; KHL – коэффициент долговечности.
KHL = (NH0 / NH) 1/6,
где NH0 – базовое число циклов нагружения; для данных сталей NH0 = 26400000;
NH = 60 · n · c · tS
Здесь:
– n – частота вращения, об./мин.; nшест. = 465,242 об./мин.; nкол. = 186,097 об./мин.
– c = 1 – число колёс, находящихся в зацеплении;
tS = 20000 ч. – продолжительность работы передачи в расчётный срок службы.
Тогда:
NH (шест.) = 60 · 465,242 · 1 · 20000 = 558290400
NH (кол.) = 60 · 186,097 · 1 · 20000 = 223316400
В итоге получаем:
КHL (шест.) = (26400000 / 558290400) 1/6 = 0,601
Так как КHL (шест.)<1.0, то принимаем КHL (шест.) = 1
КHL (кол.) = (26400000 / 223316400) 1/6 = 0,701
Так как КHL (кол.)<1.0, то принимаем КHL (кол.) = 1
Допустимые контактные напряжения:
для шестерни [sH1] = 630 · 1 / 1,1 = 572,727 МПа;
для колеса [sH2] = 600 · 1 / 1,1 = 545,455 МПа.
Для прямозубых колес за расчетное напряжение принимается минимальное допустимое контактное напряжение шестерни или колеса.
Тогда расчетное допускаемое контактное напряжение будет:
[sH] = [sH2] = 545,455 МПа.
Принимаем коэффициент симметричности расположения колес относительно опор по таблице 3.5 [1]: KHb = 1,25.
Коэффициент ширины венца по межосевому расстоянию принимаем: yba = b / aw = 0,25, (см. стр. 36 [1]).
Межосевое расстояние из условия контактной выносливости активных поверхностей зубьев найдем по формуле 3.7 гл. 3 [1]:
aw = Ka · (u + 1) · (T2 · KHb / [sH] 2 · u2 · yba) 1/3 =
49.5 · (2,5 + 1) · (533322,455 · 1,25 / 545,4552 · 2,52 · 0,25) 1/3 = 195,371 мм.
где для прямозубых колес Кa = 49.5, передаточное число передачи u = 2,5; T2 = Тколеса = 533322,455 Н·мм – момент на колесе.
Ближайшее значение межосевого расстояния по ГОСТ 2185–66 будет: aw = 180 мм.
Нормальный модуль зацепления берем по следующей рекомендации:
mn = (0.01…0.02) · aw мм, для нас: mn = 1,8.. 3,6 мм, принимаем:
по ГОСТ 9563–60* (см. стр. 36 [1]) mn = 2 мм.
Задаемся суммой зубьев:
SZ = z1 + z2 = 2 · aw / mn = 2 · 180 / 2 = 180
Числа зубьев шестерни и колеса:
z1 = SZ / (u + 1) = 180 / (2,5 + 1) = 51,429
Принимаем: z1 = 51
z2 = SZ – z1 = 180 – 51 = 129
Угол наклона зубьев b = 0o.
Основные размеры шестерни и колеса:
диаметры делительные:
d1 = mn · z1 / cos(b) = 2 · 51 / cos(0o) = 102 мм;
d2 = mn · z2 / cos(b) = 2 · 129 / cos(0o) = 258 мм.
Проверка: aw = (d1 + d2) / 2 = (102 + 258) / 2 = 180 мм.
диаметры вершин зубьев:
da1 = d1 + 2 · mn = 102 + 2 · 2 = 106 мм;
da2 = d2 + 2 · mn = 258 + 2 · 2 = 262 мм.
ширина колеса: b2 = yba · aw = 0,25 · 180 = 45 мм;
ширина шестерни: b1 = b2 + 5 = 45 + 5 = 50 мм;
Определим коэффициент ширины шестерни по диаметру:
ybd = b1 / d1 = 50 / 102 = 0,49
Окружная скорость колес будет:
V = w1 · d1 / 2 = 48,72 · 102 · 10–3 / 2 = 2,485 м/c;
При такой скорости следует принять для зубчатых колес 8-ю степень точности.
Коэффициент нагрузки равен:
KH = KHb · KHa · KHv.
Коэффициент KHb=1,049 выбираем по таблице 3.5 [1], коэффициент KHa=1 выбираем по таблице 3.4 [1], коэффициент KHv=1,05 выбираем по таблице 3.6 [1], тогда:
KH = 1,049 · 1 · 1,05 = 1,101
Дата: 2019-11-01, просмотров: 408.