Методика обучения доказательству в математике (при преподавании математике в школе) рекомендует как можно раньше приобщать школьников к самостоятельному открытию фактов и способов их обоснования, хотя у учащихся еще нет даже самого простого представления о процессе доказательства, его составляющих. Само требование «доказать» не вызывает у них нужных ассоциаций. Процесс самостоятельного поиска доказательства основывается на ряде логических и эвристических операций, многими из которых учащиеся 6–7-х классов не владеют. Поэтому на первых уроках геометрии 7-го класса следует воспользоваться готовыми доказательствами с целью изучения структуры логического вывода (наличия большой посылки, малой посылки), связей логических шагов. Для достижения этой цели можно воспользоваться специальными карточками с двумя колонками, в одной из которых указываются утверждения, в другой — обоснования, причем каждая колонка имеет пустые места, количество которых зависит от способностей школьника, заполняющего пропуски в колонках. Ясно, что сказанное не отменяет эвристического обучения и приобщения учеников к открытию доказательств. Однако самостоятельное доказательство должно основываться на понимании готового доказательства, порядка, что ведет к формированию устойчивых математических образов.
Учитывая, что у ученика с его взрослением развиваются пространственные представления об окружающем мире, приобретающие форму устойчивых образов реальных объектов, изучение элементов геометрии в 5–6-х классах естественно должно основываться на идее фузионизма (слияния); однако эта идея не должна быть стержневой. В основной школе должен изучаться систематический курс планиметрии, а в старших классах — курс стереометрии. Заканчивать изучение геометрии в средней школе следует знакомством школьников с аксиоматическим методом не только как методом организации математической теории, но и как эффективным эвристическим средством, а также выходом в геометрию четырехмерного пространства. Известно, что необходимость систематических курсов оспаривается некоторыми математиками и методистами. Они предлагают, в частности, единый курс планиметрии и стереометрии. Однако такой курс построить на достаточно строгом логическом уровне в основной школе невозможно. Такой курс будет представлять собой набор различных фактов, поэтому мера порядка его организации будет невысокой, а потому будет низкой и мера привлекательности такого курса для учащихся, что, несомненно, будет отражаться на их интересе к изучению такого курса, а следовательно и на знаниях и умениях школьников.
Необходимость учета зависимости меры красоты и привлекательности объекта от порядка и меры усилий на его понимание подтверждает и природа распознавания объектов: на уровне свернутого выполнения действий распознавание осуществляется не по логическим признакам, а по внешне выраженным, наглядным признакам используемых объектов. «Идеальный» вариант возникает тогда, когда определение понятия позволяет воображению легко конструировать образы определяемых объектов. В данном контексте, например, наиболее привлекательным среди возможных определений параллелограмма является классическое определение, так как оно в большей мере соответствует имеющемуся в мышлении ученика образу параллелограмма.
Известны многолетние дискуссии по вопросу использования алгебраического метода решения текстовых задач. Одни участники дискуссий выступают за раннее введение метода уравнений, другие считают, что основное внимание в начальной школе и в 5–6-х классах должно уделяться арифметическому методу.
С позиции красоты вряд ли будет казаться привлекательным для ученика 5-го класса решение текстовой задачи с применением уравнений или доказательство теоремы методом «от противного», потому что рассуждения, осуществляемые в процессе решения задачи либо в доказательстве теоремы, не будут для ученика естественными. Хотя текстовые задачи привлекательны для школьников, поскольку они отражают реальные ситуации, хорошо знакомые им[9].
Изначальным стимулом развития математического знания является потребность в решении конкретных практических задач, которая «неизбежно приобретает внутренний размах и выходит за рамки непосредственной полезности». Поэтому использование текстовых задач в обучении математике на ранних этапах необходимо, однако спешить с применением уравнений при их решении не следует. Последнее предполагает ряд таких умений (моделировать словесно заданные ситуации, выражать заданные величины одну через другую и т. д.), которые как раз и формируются при решении текстовых задач арифметическим способом[10]. Ученик, овладевший хотя бы некоторым опытом решения текстовых задач арифметическим методом, при встрече с алгебраическим методом будет, в какой-то мере, удивлен оригинальностью суждения при его использовании, и эта неожиданность будет усиливать привлекательность алгебраического метода.
Анализируя учебники геометрии для основной школы, можно увидеть, что метод «от противного» используется при решении задач уже на первых уроках геометрии, хотя учащиеся еще не осознали смысл прямого обоснования. Поэтому в такой ситуации применение этого метода может вызвать лишь неприязнь к изучению геометрии. Последнему будет способствовать и неопределенность требований первых задач курса геометрии.
Как уже было отмечено, важной характеристикой меры красоты является порядок, который выступает в различных формах. Наиболее распространенной из них является симметрия. Причем речь идет не только о симметрии как гармонии частей целого, их упорядоченности, но и как осознании стройности математических доказательств. Поэтому наиболее привлекательными для учащихся являются изящные доказательства. Отметим и такие характеристики красоты математики, как возможность влияния на дальнейшее продвижение в той или иной области на основе аналогии и обобщения, богатство возможных приложений как в математике, так и в смежных дисциплинах, оригинальность.
Под влиянием конкретной ситуации в коре головного мозга актуализируются определенные образы, бессознательно «ждущие» встречи с соответствующими объектами. Когда ожидание, основанное на обобщенном стандарте, беспрепятственно реализуется, это переживается как красота. В ситуации, когда воспринимаемый стимул похож на его корковую модель, но не укладывается в нее полностью, возникает удивление и связанный с ним познавательный интерес. Абсолютно новый стимул не вызывает интереса, поскольку он не представлен в психике, нет его стереотипного образа в голове. В связи со сказанным, в обучении важно использование различных рисунков к доказательству теоремы, упражнений на распознавание объектов, принадлежащих формируемому понятию, различных способов доказательства, самостоятельного открытия теорем, оригинальных способов решений, укрупнения единиц, чертежей с одной основой, аналогичных задач, блоков «родственных» задач и т. д. Все это непосредственно связано с красотой, с механизмами эстетического воспитания школьников средствами математики, с выработкой эстетического вкуса путем формирования стандартов (устойчивых математических образов).
Рассмотрим конкретные примеры.
1. Дан прямоугольный треугольник ABC с прямым углом B. На его гипотенузе AC (вне его) построен квадрат ACDE с центром O. Доказать, что луч BO является биссектрисой угла ABC.
Возможно, что кто-то из учащихся, решавших эту задачу, и предложит один из способов ее решения. Однако может оказаться, что таких учащихся не найдется. В таком случае можно предложить рассмотреть частный случай, обусловленный тем, что треугольник ABC будет прямоугольным и равнобедренным. Чертеж, иллюстрирующий данную ситуацию, будет более привлекателен для учащихся, так как его восприятие в большей мере соответствует их житейским образам. Поэтому к такому рисунку будет проявлено большее любопытство.
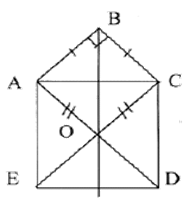
Рисунок 1
Легко заметить, что фигура на рис.1 симметрична относительно прямой BO. Этот факт легко может быть и обоснован: точка B равноудалена от точек A и C, следовательно, она принадлежит оси симметрии этих точек. Аналогично, этой же оси симметрии принадлежит и точка O. Значит, прямая BO — ось симметрии четырехугольника ABCO, а потому луч BO является биссектрисой угла B. Ясно, что обоснование доказываемого утверждения может быть выполнено и другим способом.
Устанавливаем, что четырехугольник ABCO — квадрат, около которого можно описать окружность. По отношению к ней углы ABO и OBC являются вписанными, опирающимися на равные дуги AO и OC (рис. 2). Легко заметить, что перемещая точку B по окружности (рис. 3), приходим к рис. 4, который и соответствует данной задаче. Частный случай подсказал способ ее решения. Ясно, что идея симметрии в общем случае не срабатывает, однако она наталкивает на идею использования поворота вокруг точки O на 90°.
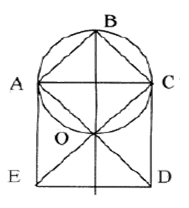
Рисунок 2
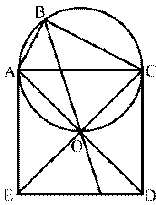
Рисунок 3
Пусть это будет поворот по часовой стрелке. Он переведет прямую AB в прямую BC, поскольку точка A перейдет в точку C, а прямая AB — в прямую, проходящую через точку C перпендикулярно к AB, то есть в прямую BC. Следовательно, точка O равноудалена от прямых AB и BC, а потому принадлежит оси симметрии угла ABC.
Решив данную задачу, следует обратить внимание учащихся на эвристики:
1) если в задачной ситуации имеется два прямоугольных треугольника с общей гипотенузой, то полезно для решения задачи ввести окружность, описанную около этих треугольников;
2) если в условии задачи даны две взаимно перпендикулярные прямые либо квадрат, то для ее решения можно воспользоваться поворотом вокруг центра квадрата на 90°.
Далее можно предложить рассмотреть случай, когда квадрат, построенный на гипотенузе AC, содержит точку B. В зависимости от уровня подготовленности класса можно продвинуться и далее. Например, прямоугольный треугольник можно заменить двумя взаимно перпендикулярными прямыми, проходящими через соседние вершины квадрата. Можно предложить учащимся составить несколько аналогичных задач, заменив квадрат, например, правильным треугольником. В этом случае две взаимно-перпендикулярные прямые должны быть заменены двумя прямыми, проходящими через соседние вершины треугольника и образующими угол в 120°. Указанная задачная ситуация может быть обобщена на правильный шестиугольник и т. д.
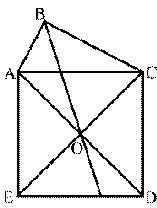
Рисунок 4
Можно заметить, что исследование задачной ситуации с использованием обобщения, конкретизации и аналогии способствует созданию обобщенного образа этой ситуации, особенно в том случае, когда она является опорной, то есть используемой в большинстве задач изучаемого раздела. Встреча учащихся с рисунком, который отложился в памяти ученика, вызовет те ассоциации, которые были связаны с ним ранее и могут продвинуть решение задачи. Наконец отметим и то, что поиск решения задачи осуществляется посредством приема мысленного преобразования исследуемого объекта, что важно, потому что данный прием является эффективным эвристическим приемом в математическом познании. С другой стороны, решение подобных задач формирует сам указанный прием, а также приемы обобщения, аналогии, конкретизации и т. п.
2. Дан равнобедренный прямоугольный треугольник ABC (∟C = 90°). Построен отрезок CC1 (C1AB), перпендикулярный медиане AA1. Найти отношение BC1 : C1A.
Данная задача интересна тем, что допускает различные способы решения, хотя заключительный этап ее решения не богат возможностями конструирования новых задач. В журнале «Математика в школе» (№ 4/1981, с. 69[11]) приведено пять способов решения задач, однако среди них нет самого простого способа, основанного на использовании координатного метода. Приведем его.
Введем систему координат так, чтобы прямая CA служила осью Ox, прямая CB — осью Oy (луч CA определяет положительное направление оси Ox, а луч CB — оси Oy); за единицу измерения примем длину отрезка AC.
Тогда
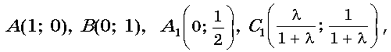
где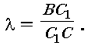 
.
Уравнение прямой CC1 имеет вид: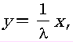 
а уравнение прямой A1A –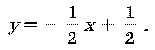 
Используя условие перпендикулярности прямых, получаем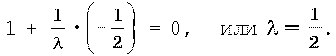 
Заключительный этап решения задачи обладает большим эстетическим потенциалом и служит хорошим средством формирования мотивации учебной деятельности школьника. Данный этап имеет значительные возможности для приобщения школьников к составлению задач, что связано с исследованием задачной ситуации.
3. Если хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой.
Конкретизация задачной ситуации приведет к задаче, в условии которой хорды перпендикулярны и одна из них является диаметром. Поскольку в полученной задаче используется частный случай, то решение последней задачи распространяется и на решение полученной. Данная задачная ситуация может быть интерпретирована по-другому: из точки окружности проведен перпендикуляр к ее диаметру. Квадрат перпендикуляра равен произведению отрезков диаметра. Заметим, что конкретизация приводит к ситуации, когда имеется решение задачи, а сама задача должна быть сформулирована.
Обобщение основной задачи приводит к ситуациям:
1) прямые, которым принадлежат хорды, пересекаются вне круга, определяемого данной окружностью;
2) одна из секущих является касательной (предельный случай 1);
3) обе секущие являются касательными.
Далее возможен выход в задачную ситуацию, которую составляют две окружности и хорды каждой из них. Требуется найти такое положение точки пересечения хорд, которое удовлетворяет основной задаче. Возможен выход даже в три окружности, что обусловит уже исследование со всеми его атрибутами.
Привлекательность работы с задачей может быть повышена даже в процессе решения элементарных задач.
Рассмотрим задачу. В треугольнике ABC биссектриса угла C пересекает сторону AB в точке D, AD = DC, ∟A = 40° (рис. 5). Доказать, что AB > BC.
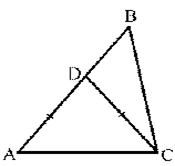
Рисунок 5
Поскольку в треугольнике ABC известен угол A, то сравнение указанных сторон может быть осуществлено посредством сравнения углов, лежащих против данных сторон. На данную эвристику следует обратить внимание учащихся. Однако ее использование требует знания второго угла треугольника — угла C. Рисунок помогает увидеть, что ∟C содержит ∟ACD, равный углу A. Таким образом, ∟C >∟A, следовательно AB > BC.
Ясно, что приведенная задача не обладает возможностями построения на ее основе задач-обобщений, задач-конкретизаций, задач-аналогов и так далее. Однако на ее основе возможно конструирование целой серии задач. Вот требования некоторых из них (условия задач совпадают с условием данной задачи):
«Сформулируйте несколько утверждений, справедливость которых следует из условия данной задачи».
Ответ: 1) ∟ACD=40°; 2) ∟C=80°; 3) ∟B=60°; 4) AC>BC; 5) AC<AB; 6) DC>BD; 7) AB>BC.
Рассмотрим следствие 7). Доказано, что AB>BC. Учитывая, что точка D находится между точками A и B, а AD=AB, то AD+BC>BC и, наконец, DC+DB>BC. Последнее неравенство, как легко заметить, будет справедливым при любой величине угла A и любом положении внутреннего луча CD. Важно лишь то, что AD=DC. Так приходим к обобщенной задаче: «На стороне AB треугольника ABC взята точка D так, что AD=DC. Докажите, что AB>BC». Данное неравенство DC+DB>BC приводит к выводу, что в треугольнике сумма двух сторон треугольника больше третьей стороны. Решение данной задачи не только мотивирует введение теоремы о неравенстве треугольников, моделирует ее доказательство, но и обосновывает ее для частного случая.
Сопровождая решение даже таких простых задач указанной работой с ними, мы повышаем их привлекательность и эстетический потенциал. Учащиеся начинают смотреть на задачи как на исследовательские объекты, в которых скрыта гармония и красота математики, наслаждаясь тем, что в процессе работы эти качества математики обнажаются, и красота математики становится для учащихся доступной.
Таким образом, красота математики раскрывается в воспитании склонности школьников к использованию обобщения и аналогии, наглядной выразительности математических объектов, унификации и разнообразным приложениям тех или иных математических фактов и закономерностей, всестороннему анализу изучаемых ситуаций, минимально возможной субъективной сложности, требуемой для достижения того или иного результата, поиску различных способов решения задачи и выбору из них наиболее изящного, полной логической обоснованности и доказательности, склонности к поиску различных моделей рассматриваемых ситуаций, общности исходных гипотез, различных приложений изучаемых фактов.
Заключение
В работе в соответствии с поставленной целью решены следующие задачи:
- рассмотрено понятие доказательства в математике и его особенности;
- рассмотрена эвристика как метод научного познания;
- рассмотрены особенности эвристического подхода в рамках логического;
- рассмотрено применение эвристических логических подходов к построению математических доказательств при изучении математики.
По работе можно сделать следующие выводы:
Математическое доказательство представляет рассуждение, имеющее задачей обосновать истинность какого-либо утверждения.
При характеристике математического доказательства выделяют две основные особенности. Прежде всего, то, что математическое доказательство исключает какие-либо ссылки на эмпирию. Вторая особенность математического доказательства - его наивысшая абстрактность, которой оно отличается от процедур доказательства в остальных науках.
Если все известные методы решения задач разделить по признаку доминирования логических эвристических (интуитивных) процедур и соответствующих им правил деятельности, то можно выделить две большие группы методов:
а) логические методы - это методы, в которых преобладают логические правила анализа, сравнения, обобщения, классификации, индукции, дедукции и т. д.;
б) эвристические методы.
Для того чтобы разобраться более глубоко в том, что понимать под эвристическими методами, следует обратить внимание на то, что метод словесно можно представить в виде некоторой системы правил, то есть описания того, как нужно действовать и что нужно делать в процессе решения задач определенного класса. Из разнообразного набора правил деятельности в решении задач принципиально можно выделить два больших класса предписаний: алгоритмы или алгоритмические предписания и эвристики - эвристические предписания. Если алгоритмы жестко детерминируют наши действия и гарантируют в случае их точного выполнения достижение успеха в решении соответствующего типа задач, то эвристики и эвристические предписания лишь задают стратегии и тактике наиболее вероятное направление поиска идеи решения, но не гарантируют успеха решения.
Эвристикой называют совокупность приемов и методов, облегчающих и упрощающих решение познавательных, конструктивных, практических задач. Эвристикой называют также специальную научную область, изучающую специфику творческой деятельности. Эвристические методы противопоставляются рутинному, формальному перебору вариантов по заданным правилам. В сущности, при решении любой задачи человек всегда использует те или иные методы, сокращающие путь к решению, облегчающие его нахождение. Напр., при доказательстве теорем геометрии мы обычно используем в качестве эвристического средства чертеж; решая математическую задачу, мы стараемся вспомнить и использовать решения других похожих задач; в качестве эвристических средств используются общие утверждения и формулы, индуктивные методы, аналогии, правдоподобные умозаключения, наглядные модели и образы, мысленные эксперименты и т. п.
Использование эвристических подходов при построении математических доказательств помогает не только преобразовывать существующую информацию и сохранять ее истинностное значение, но и искать новую информацию с помощью особых форм рассуждения. Применение эвристических подходов в математике предполагает использование обобщения и аналогии, наглядной выразительности математических объектов, унификацию и разнообразные приложения тех или иных математических фактов и закономерностей, всесторонний анализ изучаемых ситуаций, минимально возможную субъективную сложность, требуемой для достижения того или иного результата, поиск различных способов решения задачи и выбору из них наиболее изящного, полную логическую обоснованность и доказательность, склонность к поиску различных моделей рассматриваемых ситуаций, общность исходных гипотез, различных приложений изучаемых фактов.
Список литературы
1. Адамар Ж. Исследование психологии процесса изобретения в области математики. — М., 1970.
2. Белл Э.Т. Творцы математики. — М., 1979.
3. Беляев Е.А, Перминов В.Я. «Философские и методологические проблемы математики», МГУ, 1981, - 214 с.
4. Биркгоф Г. Математика и психология. — М., 1977.
5. Болтянский В.Г. Математическая культура и эстетика. — // Математика в школе, № 2/1982, с. 40–43.
6. Заесенок В. П. Эвристические приемы решения логических задач // Математика в школе. - 2005. - N 3.
7. Калошина И.П., Миничкина Н.В. Логические приемы мышления как условие самостоятельной разработки студентами способов доказательства теорем. - В кн.: Подготовка учителя математики в университете. Саранск, 1984, c.22 - 33.
8. Калошина И.П., Харичева Г.И. Логические приемы мышления при изучении высшей математики. - Воронеж: Изд-во Воронежского ун-та, 1978. - 128 с.
9. Курант Р., Робинс Г. Что такое математика? — М., 1967.
10. Лакатос И. Доказательства и опровержения. М., 1967.
11. Миничкина Н.В. Формирование логических приемов мышления как условия самостоятельной познавательной деятельности студентов. - Дис. ... канд. пед. наук. Саранск, 1984.-268 с.
12. Писаревский Б. М. Задачи по стереометрии. Правильная пирамида // Математика в школе. - 2005. - N 3.
13. Саранцев Г.И.Обучение математическим доказательствам в школе: Книга для учителя. – М.: "Просвещение" – 2000. - 173 с.
14. Серебряников О.Ф. Эвристические принципы и логическое мышление. М.: 1979.
15. Шакуров Р.Х. Эмоция. Личность. Деятельность (механизмы психодинамики). — Казань, 2001.
16. Эвристические приемы при построении доказательств //Математика в школе», 1981. - № 4/1981, с. 69
[1] Серебряников О.Ф. Эвристические принципы и логическое мышление. М.: 1979. – с. 111
[2] Серебряников О.Ф. Эвристические принципы и логическое мышление. М.: 1979. – с. 48-49.
[3] Лакатос И. Доказательства и опровержения. М., 1967. – с. 84.
[4] Белл Э.Т. Творцы математики. — М., 1979. – с. 63.
[5] Биркгоф Г. Математика и психология. — М., 1977. – с. 54.
[6] Болтянский В.Г. Математическая культура и эстетика. — // Математика в школе, № 2/1982, с. 40–43.
[7] Шакуров Р.Х. Эмоция. Личность. Деятельность (механизмы психодинамики). — Казань, 2001. – с. 87
[8] Эвристические приемы при построении доказательств //Математика в школе», 1981. - № 4/1981, с. 69
[9] Курант Р., Робинс Г. Что такое математика? — М., 1967. - с. 88
[10] Шакуров Р.Х. Эмоция. Личность. Деятельность (механизмы психодинамики). — Казань, 2001. – с. 88
[11] Эвристические приемы при построении доказательств //Математика в школе», 1981. - № 4/1981, с. 69
Дата: 2019-11-01, просмотров: 182.
