Индексирование матриц является средством доступа к подмножеству элементов матриц, которое позволяет извлекать из матриц подмножества их элементов, присваивать извлеченное из матриц подмножество новым матрицам и модифицировать подмножество элементов существующих матриц. В Scilab имеется несколько способов индексирования, которые влияют не только на скорость выполнения программного кода, но и на его читаемость. Таким образом, индексирование является ключевым моментом эффективности использования средств пакета Scilab при реализации матричных операций. Причем индексирование тесно связано с понятием векторизации [12].
Векторизация означает использование таких конструкций программной системы, которые позволяют отказаться от операторов for , whil eи других, используемых для организации явных циклов программы. Причем векторизация обычно приводит к тому, что программа начинает работать быстрее. Большинство из возможных подходов к векторизации используется и при индексировании матриц Scilab.
Обычно поэлементные операции над матрицами выполняются для всех элементов матриц одного размера (одинаковой размерностью и с одинаковым числом элементов по каждому измерению). В некоторых случаях возможно выполнять операции над матрицами разного размера за счёт неявного расширения одной из матриц, которое является одним из элементов векторизации.
Следует помнить, что нумерация элементов матрицы в строках и столбцах начинается с 1 , а также, что операция [] и соответствующие функции всегда создают двумерную матрицу, включая матрицы 0×0, 0×n, n×0, 1×1 и 1×n
Индексирование векторов
Индексирование векторов– это стандартный подход к индексированию одним индексом, который используется во всех языках программирования:
V 1(НомерЭлементаСтроки)
V 2(НомерЭлементаСтолбца),
где V 1 – вектор строка, V 2 – вектор столбец иV 2=V 1'.
Рассмотрим Примеры1-11 на рис. 1.3.3-1, иллюстрирующие особенности использования индексации в Scilab.
--> // Примеры индексирования векторов
-->
--> vA1 = [40 5 13 4 2 11 7 14] // Создание вектора 1×8
-->
--> // Пример1 Доступ к одному элементу вектора
--> vA1(3) // Доступ к третьему элементу вектора
ans =
13.
-->
--> // Пример2 Доступ к нескольким элементам вектора
--> vA1([1 5 6]) // Доступ к 1, 5 и 6 элементам вектора
ans =
40. 2. 11.
-->
--> // Пример3 Доступ от 3-го до 7-го элемента вектора
--> vA1(3:7)
ans =
13. 4. 2. 11. 7.
-->
-->// Пример4 Доступ, извлечение и создание нового вектора
--> vA2 = vA1([5:8, 1:4])
vA2 =
2. 11. 7. 14. 40. 5. 13. 4.
-->
--> // Пример5 Доступ к последнему элементу вектора
--> vA1($)
ans =
14.
-->
--> //Пример6 Доступ от 5-го элемента вектора до последнего
--> vA1(5:$)
ans =
2. 11. 7. 14.
-->
--> //Пример7 Использование $ в арифметических операциях
--> vA1(2:$ - 1) //Доступ от 2-го до7-го элемента (предпоследнего)
ans =
5. 13. 4. 11. 7.
-->
--> // Пример8 Доступ ко всем нечетным элементам вектора
--> vA1(1:2:$)
40. 13. 2. 7.
-->// Пример9 Обратный порядок доступа к элементам вектора
--> vA1($:-1:1)
ans =
14. 7. 11. 2. 4. 13. 5. 40.
-->// Пример10 Модификация элементов существующего вектора
--> vA1([2 3 4]) = [10 15 20]
vA1 =
40. 10. 15. 20. 2. 11. 7. 14.
-->
--> // Пример11Скалярное расширение (присвоение значение 30 2 и 3 элементу)
--> vA3([2 3])' = 30 // Замена 2-го и 3-го элементов на значение 30
vA3 =
0.
30.
30.
Рис. 1.3.3-1. Примеры векторного индексирования
Стандартное индексирование матриц
Стандартное индексирование матриц реализуется с помощью двух индексов. Матричное стандартное индексирование предполагает использование двух индексов, разделенных запятой – первой для строк, а второй для столбцов, причем не надо забывать, что индексирование начинается с 1:
mA(НомерЭлементаСтроки, НомерЭлементаСтолбца).
Создадим матрицу mA (4,4) и проиллюстрируем на ней использование матричной индексации (Примеры 1-4 на рис. 1.3.3-2).
--> // Примеры матричной индексации
-->
--> mA = [16 2 3 13; 5 11 10 8; 9 7 6 12; 4 14 15 1]
mA =
16. 2. 3. 13.
5. 11. 10. 8.
9. 7. 6. 12.
4. 14. 15. 1.
-->
--> // Пример1 Доступ к одному элементу в строке 2 и столбце 4
--> mA(2, 4)
ans =
8.
-->
--> // Пример2 Доступ к подмножеству элементов (индексы являются векторами)
--> mA(2:4, 1:2)
ans =
5. 11.
9. 7.
4. 14.
-->
--> // Пример3 Доступ к элементам 3-ей строки, используя операцию :
-->
--> A(3, :)
ans =
9. 7. 6. 12.
-->
--> // Пример4 Доступ к последнему столбцу
--> mA(:, $)
ans =
13.
8.
12.
1.
|
Рис. 1.3.3-2. Примеры стандартной матричной индексации
Векторное (линейное) индексирование матриц
Линейное векторное индексирование матриц, это такое индексирование матриц, при котором индексирование ее элементов осуществляется только одним индексом. В этом случае матрицу рассматривают как суммарный вектор, составленный из векторов матрицы, то есть вектор, в котором все элементы матрицы вытянуты в один длинный вектор-столбец, где каждый следующий столбец индексируемой матрицы следует за предыдущим столбцом
(рис. 1.3.3-3). Так на самом деле матрица хранится в памяти (в нашем случае это последовательность: 1 5 9 2 6 10 37 11 4 8 12). Следовательно, двумерные массивы располагаются в Рабочей области данных по столбцам.
| Значения элементов | Линейные индексы | Матрица mA | ||||||||||||||||||||
| 1 5 9 2 6 10 3 7 11 4 8 12 | 1 2 3 4 5 6 7 8 9 10 11 12 |
|
Рис. 1.3.3-3. Элементы матрицы и их линейные индексы
Индексирование матриц одним индексом называется линейным
векторным индексированием матриц. Например, выражение mA (8) просто извлекает 8-й элемент неявного вектора-столбца.
Примеры линейного индексирования матриц приведены на рис. 1.3.3-4.
--> // Примерылинейной матричной индексации
-->
--> mA = [16 2 3 13; 5 11 10 8; 9 7 6 12; 4 14 15 1];
--> // Пример1
--> mA([2 7 16]) // Доступ ко 2-му, 7-му и 16-му элементу линейной матрицы
ans =
5.
7.
1.
--> // Пример2 Преобразование индексы матрицы в линейные индексы
--> idmA = sub2ind(size(mA), [2 3 4], [1 2 4])
idmA =
2. 7. 16.
-->mA(idmA)
ans =
5.
7.
1.
--> // Пример3 Преобразование из матричного представление в векторное
--> A = [2 6 9; 4 2 8; 3 5 1];
--> linearindex = sub2ind(size(A), 3, 2)
linearindex =
6.
-->A(linearindex)
ans =
5.
Рис. 1.3.3-4 Примерылинейнойиндексацииматриц
В Примере1 показано, что индекс при линейном индексировании матрицы может быть вектором, содержащим более одного линейного индекса, и в этом случае они должны быть перечислены через пробелы или запятые и заключены в квадратные скобки. По заданным линейным индексам производится доступ и извлечение значений элементов матриц.
В Примере2 проведено преобразование индексов матрицы в линейные индексы. Чтобы получить эквиваленты линейных индексов строки и столбца, была использована функция ind2sub, имеющая три параметра: размер матрицы ( size(A) ); индексы строк ( [2 3 4] )и индексы столбцов ( [1 2 4] ). То есть в этом примере нас интересуют линейные индексы таких элементов матрицы, которые при обычном стандартном индексировании записаны как mA (2,1), mA (3,2) и mA (4,4).Чтобы получить линейный индекс одного элемента воспользуемся формулой перерасчета, по которой собственно и происходит расчет в системе Scilab: iV=(j-1)*d1+i,где i и j – номера, соответственно, строки и столбца элемента матрицы, а d1 – размер матрицы. Рассчитаем, например, линейный индекс 1-го заданного в примере элемента: i=2, j=1, d1=3, а iV=(1–1)*3+2=2. Далее показана возможность извлечения элементов по их линейным индексам.
В Примере3 проведено преобразование индексов одного элемента матрицы ( 3х3 ) к его линейному эквиваленту и извлечение с его помощью элемента массива.
Таким образом, для доступа к элементам матриц есть выбор между использованием стандартного матричного синтаксиса и использованием доступа, который называется векторным (линейным) индексированием. Предполагая, что A(i,j) элемент матрицы A размерности n×m, индекс этого же элемента A(k) при линейной индексации можно рассчитать по формуле k=(j-1)*n+i.
Функции sub2ind и ind2sub позволяют осуществить преобразования, соответственно, из линейного индексирования элементов матрицы в матричную и из матричной в линейную (Приложение 1.3, табл. 1.3.3-1).
В общем виде возможны два случая индексирования одной матрицы другой матрицей. В первом случае оно основано на значе ниях элементов индексирующего массива, а во втором – индексирование основано на позициях элементов индексирующей матрицы, и поэтому называется логическим
индексированием.
В примерах на рис.1.3.3-2мы фактически уже сталкивались с первым случаем индексирования одного массива другим массивом. Рассмотрим еще несколько примеров (Примеры1-5, рис. 1.3.3-5),иллюстрирующих индексирование, основанное на значениях.
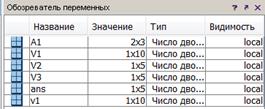
Так, в Примере1 (рис. 1.3.3-5) значения элементов вектора V2 являются индексами вектора V1. В Примере2 показано, что результат индексирования не зависит от того, является индексирующий вектор столбцом или строкой. В Примере3 показано, что результат индексирования зависит от того является индексируемый вектор столбцом или строкой. В Примере4 показано индексирование матрицы А1 вектором V 3.
--> // Примеры индексирования матрицы
--> // значениями элементов вектора
-->
--> // Пример1
--> V1 = 5:5:50
V1 =
5. 10. 15. 20. 25. 30. 35. 40. 45.50.
--> V2 = [1 3 6 7 10];
--> V1(V2)
ans =
5. 15. 30. 35. 50.
-->
--> // Пример2
--> V1(V2')
ans =
5. 15. 30. 35. 50.
-->
--> // Пример3
--> V3 = V1';
-->V3(V2)
ans =
5.
15.
30.
35.
50.
-->
--> // Пример 4
--> A1 = [1 3 6; 7 9 10];
--> V3 = [1 2 3 4 5];
--> A1(V3)'
ans =
1. 7. 3. 9. 6.
| 
|
Рис. 1.3.3-5 Индексирование матрицы другой матрицей, основанное
на значениях индексирующей матрицы (вектора)
Рассмотрим более сложный пример установки некоторого множества элементов матрицы в ноль. Например, требуется найти максимум каждой строки заданной матрицы, а потом все остальные элементы установить в ноль. Решение данной задачи представлено на рис. 1.3.3-6.
--> // Установка некоторого множества элементов матрицы в ноль
-->
-->A = [1 2 3 4; 5 5 6 7; 7 9 8 3] // Создание исходной матрицы
A =
1. 2. 3. 4.
5. 5. 6. 7.
7. 9. 8. 3.
--> // Значения y и номера I максимальных элементов в каждой строке
--> [y, I] = max(A, 'c')
I =
4.
4.
2.
y =
4.
7.
9.
-->
-->B = zeros(A) // Создание матрицы Bc нулевыми элементами
B =
0. 0. 0. 0.
0. 0. 0. 0.
0. 0. 0. 0.
-->
--> B(sub2ind(size(A), 1 : length(I), I')) = y // ФормированиематрицыB
B =
0. 0. 0. 4.
0. 0. 0. 7.
0. 9. 0. 0.
Рис. 1.3.3-6 Пример установки некоторых элементов матрицы в ноль
При доступе к элементам матрицы с числовыми индексами вне границ матрицы (присвоении значений таким элементам), Scilab расширяет (увеличивает) размерности этой матрицы для включения этих элементов в матрицу, заполняя остальные получившиеся при расширении элементы нулями. Это можно квалифицировать как добавление элементов к существующей матрице. При этом, если бы была предпринята попытка сослаться на элементы матрицы за пределами массива справа от оператора присваивания, Scilab выдал бы сообщение об ошибке: «Недопустимый индекс».
В Примере1(рис. 1.3.3-7) показано присвоение значения элементу массива А за пределами его границ. Отображение матрицы показывает, что произошло добавление 5-го столбца, где в 3-й строке присвоенное значение 7, а все остальные элементы равны 0.
Удаление элементов из существующей матрицы можно осуществить путем присвоения пустого множества этим элементам – []. Удалением элементов можно сделать вектор короче, а матрицу – меньше (Пример2,
рис. 1.3.3-7).
--> // Назначение элементов вне границ и удаление элементов матрицы
-->
-->// Исходная матрица A (4 x 4)
--> A = [16 2 3 13; 5 11 10 8; 9 7 6 12; 4 14 15 1]
A =
16. 2. 3. 13.
5. 11. 10. 8.
9. 7. 6. 12.
4. 14. 15. 1.
-->
-->A(3, 7)
Недопустимый индекс.
--> //
-->A(3, 5) = 7 // A (3,5) – вне границ массива!
A =
16. 2. 3. 13. 0.
5. 11. 10. 8. 0.
9. 7. 6. 12. 7.
4. 14. 15. 1. 0.
-->
--> // Пример2
-->A(1, :) = [] // Удаление 1-й строки
A =
5. 11. 10. 8. 0.
9. 7. 6. 12. 7.
4. 14. 15. 1. 0.
|
Рис. 1.3.3-7. Назначение и удаление элементов вне границ матрицы
Доступ к нескольким непоследовательным элементам матрицы можно
осуществить также с помощью операции двоеточие со значением шага
h(m:h:n). Так в примере (рис. 1.3.3-8), выражение B(1:3:16)=-10 означает, что каждому 3-му элементу матрицы В присваивается значение -10. Обратите внимание на то, что в этом примере используется линейное индексирование
|
--> // Доступ к нескольким элементам матрицы
-->
-->A = [1 1 1 1; 2 2 2 2; 3 3 3 3; 4 4 4 4];
-->B = A;
-->B(1:3:16) = -10
B =
-10. 1. 1. -10.
2. 2. -10. 2.
3. -10. 3. 3.
-10. 4. 4. -10.
|
Рис. 1.3.3-8. Доступ к нескольким элементам матрицы
Таким образом, обращение (индексирование) к элементам матрицы можно осуществить как с помощью операции двоеточие (:), ссылаясь на все элементы (или часть элементов) в строке (или столбце) матрицы, так и ко всем элементам матрицы (Приложение 1.3, табл. 1.3.3-2).
Дата: 2019-11-01, просмотров: 1005.
