Рассмотрим сначала общую задачу расчета будущей (наращенной) стоимости потока платежей. Введем обозначения:
Rt – размер платежа, осуществляемого в период t;
n – общий срок выплат (операции).
Необходимо определить наращенную на конец срока сумму потока платежей, если проценты начисляются раз в году по сложной ставке i.
FV = ∑ Rt*(1+i)n-t.
Современная стоимость такого потока платежей:
PV = ∑ Rt /(1+ i ) t .
Зная современную стоимость потока, можно рассчитать его будущую стоимость и наоборот: FV = PV *(1+ i ) n .
Теперь рассмотрим случай годовой ренты (аннуитета) постнумерандо. Пусть в течение n лет в банк в конце каждого года вносится сумма R (соответственно, номера платежей t меняются от 1 до n). На взносы начисляются сложные проценты по ставке i % годовых. На первый член проценты начисляются n-1 лет, на второй n-2 и т.д., на последний – n-n=0 лет, т.е. все члены ренты, кроме последнего, приносят проценты. Наращенная сумма каждого взноса к концу срока составит:
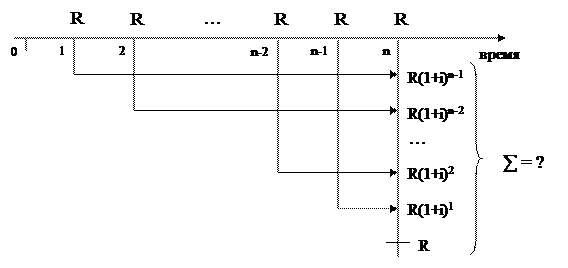 |
Запишем получившийся ряд членов в обратном порядке:
R, R(1+i)1, R(1+i)2, …, R(1+i)n-2, R(1+i)n-1
Он представляет собой геометрическую прогрессию с первым членом R и знаменателем (1+i). Число членов прогрессии равно n. Используя формулу для расчета суммы n первых членов геометрической прогрессии, получим:
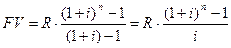
[ геом. прогрессия: a, aq, aq2, aq3 …
an = aqn-1 Sn = a 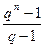 ]
]
Множитель 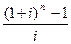 называется коэффициентом наращения ренты (аннуитета), или мультиплицирующим множителем для аннуитета, обозначается FM3(n, i). Он представляет собой наращенную сумму ренты, член которой равен 1. Значение множителя для различных величин i и n табулировано (рассчитано и представлено в специальных финансовых таблицах). Т.о., FV = R* FM3(n, i).
называется коэффициентом наращения ренты (аннуитета), или мультиплицирующим множителем для аннуитета, обозначается FM3(n, i). Он представляет собой наращенную сумму ренты, член которой равен 1. Значение множителя для различных величин i и n табулировано (рассчитано и представлено в специальных финансовых таблицах). Т.о., FV = R* FM3(n, i).
ПРИМЕР: Для обеспечения будущих расходов создается фонд. В течение 4 лет в конце каждого года на специальный счет поступает 50 000 д.е. (постоянная годовая рента постнумерандо). На поступившие взносы начисляются сложные проценты по ставке 10% годовых. Определить величину фонда на конец срока.
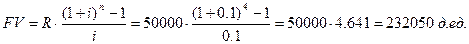
Или FV = R * FM3(n, i) = 50000 * 4.641 = 232 050 д.ед.
Приведенная выше формула может использоваться для расчетов при условии осуществления платежей и начисления процентов 1 раз в год (p=m=1).
Годовая рента, начисление процентов m раз в году ( m > p , p =1).
В данном случае ежегодный платеж будет наращиваться с учетом внутригодовых начислений. Члены ренты с начисленными к концу срока процентами перепишем в обратном порядке:
R, R(1+j/m)m, R(1+j/m)2m, …, R(1+j/m)(n-2)m, R(1+j/m)(n-1)m,
где j – номинальная годовая ставка процента.
Снова имеем дело с возрастающей геометрической прогрессией. Первый член прогрессии равен R, знаменатель - (1+j/m)m. Сумма членов этой прогрессии составляет:
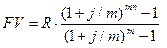
Рента р-срочная, годовое начисление процентов (р> m , m =1).
Пусть рента выплачивается p раз в году равными суммами, процент начисляется раз в конце года. Если годовая сумма платежей равна R, то каждый раз выплачивается R/p. Общее число членов ренты равно np. Последовательность членов ренты с начисленными процентами представляет собой геометрическую прогрессию. Первый член ее равен R/p, знаменатель – (1+i)1/p. Сумма членов этой прогрессии будет равна:
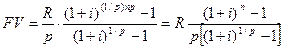
Рента р-срочная, начисление процентов m раз в году (р= m >1).
Случаи, когда число выплат в году равно числу начислений процентов, на практике встречаются наиболее часто. Для получения необходимой формулы воспользуемся исходной 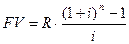 , в которой i заменим на j/m (ставка за период), вместо числа лет подставим число периодов выплаты ренты nр. Так как R – годовой платеж, то член ренты равен R/p. Поскольку р = m, в итоге получим:
, в которой i заменим на j/m (ставка за период), вместо числа лет подставим число периодов выплаты ренты nр. Так как R – годовой платеж, то член ренты равен R/p. Поскольку р = m, в итоге получим:
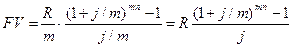
Рента р-срочная, начисление процентов m раз в году (р≠ m ).
Этот случай является наиболее общим, а вышеперечисленные – его частными вариантами. Общее количество членов ренты равно np, величина члена ренты R/p. Члены ренты с начисленными процентами образуют геометрическую прогрессию с первым членом R/p и знаменателем (1+j/m)m/p. Сумма членов такой прогрессии составит:
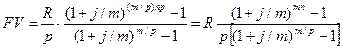
Дата: 2019-11-01, просмотров: 349.