Группа указаний, которая имеет свой законченный смысл, называется оператором.
Операторы мы будем обозначать большими буквами с индексами, Ai и т.п. Операторы классифицируется следующим образом.
1) По структурным свойствам:
а) простой; б) составной; в) циклический.
2) По характеру выполняемых действий:
а) арифметический; б) логический; в) оператор перехода (передачи управления); г) оператор ввода информации в машину; д) оператор вывода информации из машины; е) оператор обмена информацией; ж) оператор остановки и др.
Почти каждый алгоритм можно разделить на несколько групп указаний различных по назначению, т.е. операторов. Обозначив, операторы буквами, и указав последовательность выполнения операторов стрелками, мы получим операторную схему алгоритма.
Пример 3. Пусть требуется вычислить величины:
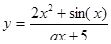 (1)
(1)
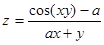 (2)
(2)
Исходными данными для решения задачи является значения переменных x , a. Обозначим оператор ввода исходных данных через B 1. Оператор вывода результата (значений y , z) через – B 2 . Оператор вычисления значения y по формуле (I) - через A 1 . Оператор вычисляющий z- по формуле (2), через – A 2. Оператор остановки процесса решения через O 1 . Переход между операторами обозначим стрелками. Тогда операторную схему алгоритма решения данной задачи можно представить следующим образом:
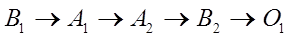
т.е. вначале следует ввести значения исходных данных – x , a (оператор B1); затем вычислить значение y (оператор A 1); вычислив значение y, требуется вычислить значение z (оператор A 2); напечатать результат - значения y , z (оператор B2) и остановить процесс – оператор О1.
Если операторы выполняются в том порядке, в котором они записаны, то стрелки можно опустить, т.е. операторную схему можно записать в следующем сокращенном виде: 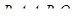 .
.
Это пример линейного алгоритма. Приведем пример разветвляющегося алгоритма.
Пример 4. Написать операторную схему алгоритма по определению корней квадратного уравнения 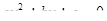 при
при  . Опишем процесс (план) решения задачи:
. Опишем процесс (план) решения задачи:
1) вычисляем значение дискриминанта, 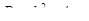 ;
;
2) сравниваем значения дискриминанта с нулем;
3) если  , то вычисляем x 1 , x 2 по формулам
, то вычисляем x 1 , x 2 по формулам
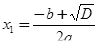 ;
; 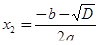 ,
,
печатаем полученные значения, и останавливаем процесс решения;
4) если  , то выводим фразу «Действительных корней нет» и останавливаем процесс решения.
, то выводим фразу «Действительных корней нет» и останавливаем процесс решения.
Запишем теперь операторную схему,
Обозначим:
B1 - оператор ввода значений a, b, c;
A1 - оператор вычисляющий дискриминант D;
P1 - оператор проверяющий условие D<0;
A2 - оператор вычисляющий значение x1;
A3 - оператор вычисляющий значение x2;
B2 - оператор вывода значений x1, x2;
B3 - оператор вывода фразы «Действительных корней нет»;
O1, O2 - операторы остановки.
|
|
 A2A3B2O1
A2A3B2O1
 B1A1P1
B1A1P1
B3O2
Циклические алгоритмы
Как было указано выше, циклическим алгоритмом является тот, у которого имеется хотя бы одна группа указаний, которая повторяется в процессе решения. Такая группа указаний называется циклическим оператором.
Различают два вида циклических операторов:
1) Циклический оператор с заданным количеством повторений;
2) Итерационный циклический оператор.
|



 A0 A1 P1 (продолжение)
A0 A1 P1 (продолжение)

A 0 - оператор или операторы подготовки цикла.
A1 - группа основных операторов, которые требуется повторить. Эту группу операторов обычно называют телом цикла.
Р1 - условный оператор, который проверяет некоторое условие и если оно выполняемся, то заставляет повторяться еще операторы тела цикла, если нет, то передает управление на продолжение алгоритма.
Управление повторением оператора цикла осуществляется с помощью некоторой переменной, которую называют параметром цикла.
В циклическом операторе первого вида параметр цикла изменяется от одной границы L1 до второй границы L2 с некоторым постоянным интервалом (шагом) h за каждым повторением. В этом случае легко вычислить количество повторений k:
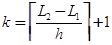
В итерационном цикле параметр цикла также меняет свое значение при повторениях, но интервал изменения может быть не задан заранее и выбираться в процессе повторений, а с другой стороны оператор Р , может проверять условие, момент невыполнения, которого заранее нельзя предсказать.
В операторе A0 осуществляется подготовка цикла, т.е. параметр цикла и величины, которые изменяются в цикле, этими операторами приводятся в исходные значения.
Оператор P может стоять после тела цикла, как в приведенной выше схеме, или до основных операторов, т.е. перед A1. В зависимости от этого циклические операторы разделяют на два типа: циклический оператор с постусловием и циклический оператор с предусловием. Принципиальное отличие этих операторов состоит в том, что в операторе с постусловием группа основных операторов выполнится хотя бы один раз, а в операторе с предусловием тело цикла может ни разу не выполниться.
Если некоторый цикл расположен внутри другого цикла, то говорят, что имеется двойной цикл. При этом цикл, расположенный внутри, называется внутренним, а цикл, который охватывает его, внешним циклом. При двойном цикле при одном изменении .параметра внешнего цикла, параметр внутреннего цикла пробегает все свои значения. Могут быть тройные и большего количества уровней цикли.
Относительно расположения вложенных циклов существуют такие правила:
1. Внутренний цикл должен быть строго внутренним.
2. Не допускается пересечений циклов.
Для передач управления из цикла в цикл приняты следующие правила:
1. Передача управления в цикл может быть осуществлена только через его начало;
2. Выход из цикла может быть осуществлен до окончания цикла;
3. Передачи управления внутри цикла допускаются.
Операторные схемы являются довольно компактным средством изображения процесса решения задачи. Но они имеют один довольно существенный недостаток, который заключается в малой наглядности выполняемых действий. В силу этого, в настоящее время, операторные схемы, для описания алгоритмов, применяются довольно редко. Более распространенными являются блок-схемы алгоритмов. Поэтому приводить пример циклического алгоритма в виде операторной схемы мы не будем, а приведем его в виде блок-схемы, к рассмотрению которых мы переходим.
Блок-схема алгоритма
Блок-схемой алгоритма называется геометрическое представление операторной схемы алгоритма, в котором операторы изображаются в виде плоских геометрических фигур, а последовательность их выполнения указывается стрелками.
При построении блок-схемы алгоритма принята стандартная система геометрических фигур, применяемых для различных видов операторов. В таблице 1 приведены основные операторы и их геометрическое представление, соответствующее принятому стандарту.
Таблица 1. Основные операторы и их геометрическое представление, соответствующее принятому стандарту.
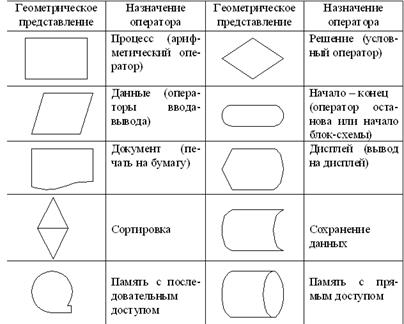
Приведем пример блок-схемы алгоритма начисления заработной платы по заданной ставке с учетом вычета подоходного налога, величина которого определяется по тарифной сетке (заметим, что пример является условным, и поэтому цифры и сама тарифная сетка не соответствуют реальности).
Пример 5. Условие задачи опишем следующим образом:
Пусть х – величина произвольной ставки. В зависимости от конкретного значения х, начисляется подоходный налог у, по следующему правилу (тарифной сетке):
· Если х меньше или равен а, то подоходный налог не начисляется, т.е. у=0.
· Если х больше а, но меньше или равен b , то подоходный налог равен 10% от х.
· Если х больше b , но меньше или равен c , то подоходный налог равен 15% от х.
· Если х больше c , то подоходный налог равен 20% от х.
Значение заработной платы, с учетом вычитаемого подоходного налога, будет z = x – y . Если описанный процесс обозначить математическими формулами, то будем иметь следующую запись:
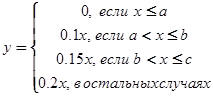 ,
,
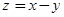 .
.
Исходными данными для рассматриваемой задачи являются значения x , a , b , c. Результатом будет значение z . Заметим, что в зависимости от требуемого, результатом может быть величина подоходного налога у и заработная плата z . Выводить на печать можно также вместе с результатами и значение х.
Блок схема алгоритма решения данной задачи представлена на рис. 4.
Алгоритмы обладают некоторыми свойствами, которые позволяют облегчить их составление для различных задач. Во-первых, многие различные по смыслу задачи, имеют сходные алгоритмы. Во-вторых, сложные алгоритмы имеют блоки (участки) алгоритмы которых известны и, при составлении общего алгоритма, достаточно вставить такой блок в свою схему, возможно с небольшими изменениями. В третьих, в сложных алгоритмах, как правило, существуют сходные участки (блоки), которые можно переписать практически без изменений. В четвертых, существует сравнительно небольшой набор, стандартных по конструкции, операторов, с помощью которых строятся сложные алгоритмы. Построение алгоритма подобно возведению здания из набора типовых конструкций.
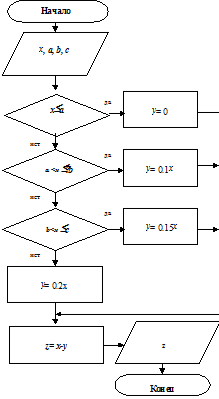
Рис. 4. Блок-схема задачи начисления подоходного налога.
Наиболее часто используемым методом построения блок-схем алгоритмов является метод последовательной декомпозиции. Суть его заключается в том, что вначале строят укрупненную схему алгоритма, каждый блок которой может представлять решение довольно сложной задачи. Затем последовательно, шаг за шагом, производят разукрупнение блоков до последовательности указаний (операторов), которые легко можно перевести в программу на алгоритмическом языке.
Пример 6. Проиллюстрируем метод декомпозиции на составлении блок-схемы алгоритма решения квадратного уравнения:
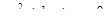
Укрупненная схема алгоритма следующая:

1. Исходными данными для задачи являются значения коэффициентов уравнения a , b , c. Разукрупнять блок «Ввод исходных данных» не надо, т.к. этот ввод можно осуществить одним оператором.
2. Блок «Нахождение решения уравнения». Для определения решения уравнения надо вначале вычислить дискриминант 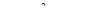 . Затем проверить знак дискриминанта. Если дискриминант больше нуля, то уравнение имеет два корня, которые вычисляются по формулам:
. Затем проверить знак дискриминанта. Если дискриминант больше нуля, то уравнение имеет два корня, которые вычисляются по формулам:
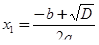 ;
; 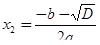 .
.
В этом случае результатом будет значения этих корней.
Если дискриминант равен нулю, то уравнение имеет один корень, который вычисляется по формуле: 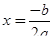 . Это значение и будет результатом в этом случае.
. Это значение и будет результатом в этом случае.
Если дискриминант меньше нуля, то уравнение не имеет действительных корней. В этом случае результатом будет фраза «Уравнение не имеет действительных корней».
Декомпозиция этого блока следующая:

3. Блок «Вывод результатов». В зависимости от значения дискриминанта, мы можем получить три результата. Поэтому этот блок по сути состоит из трех разных операторов вывода:

Приведем примеры циклических алгоритмов
Пример 7. Составим блок-схему алгоритма начисления процентов по вкладам.
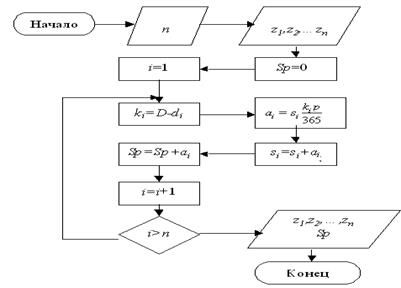
Рис. 5. Блок-схема алгоритма начисления процентов по вкладам.
Описание постановки задачи:
Имеется n записей z 1 , z 2 ,… zn, характеризующих вклады. Среди характеристик имеются следующие: si – величина вклада; di – дата последнего начисления процентов. Если по вкладу не было начислений процентов, то эта дата совпадает с датой вложения. Требуется произвести начисление процентов из условия p процентов годовых. Начисление проводится в конце некоторого периода (года, квартала) на дату, которую обозначим D. Кроме начислений по каждому вкладу, требуется определить общую сумму начисленных процентов. Суть алгоритма заключается в следующем: просматриваем записи, поочередно, начиная с первой. Для каждой записи находим количество дней, прошедших после последнего начисления процентов. Пусть это количество равно ki для i-ой записи. Тогда соответствующая сумма процентов будет определяться по формуле:
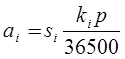
Эту сумму добавляем к si и в общую сумму начисленных процентов, которую обозначим Sp. Блок-схема алгоритма представлена на рис.3.
Пример 8. Блок–схема алгоритма сортировки. (Метод «Пузырек»).
Пусть а1,а2,…,а n есть массив записей, описывающих некоторое множество объектов. Например, а i – анкета i-го работника учреждения. Требуется упорядочить множество элементов а i по возрастанию признака pi, например, по возрасту или стажу работы.
Для сортировки используем алгоритм «Пузырек». Суть его состоит в том, что вначале просматриваются поочередно все соседние пары элементов (ai -1 , ai, i =2,3,…, n) и сравниваются признаки, по которым ведется сортировка. Если pi -1 < pi, то пара пропускается, и переходят к просмотру следующей пары (ai , ai +1). Если pi -1 > pi, то в такой паре меняются местами элементы ai -1 и ai. После просмотра последней пары, элемент обладающий наибольшим значением признака сортировки, автоматически переместится (всплывет) на последнее место. Затем просматриваются все пары без последней (an -1 , an). За каждым таким шагом, количество просматриваемых пар уменьшается на единицу. Просмотр заканчивается, когда остается одна пара.
Введем обозначения:
n – количество элементов в множестве. (входной параметр).
a 1 ,…, an – элементы (записи) множества (входной массив и он же результат).
p 1 ,…, pn – значения признака, по которому производится сортировка.
k – граница просмотра на каждом шаге (k =2,…, n).
i - текущий номер просматриваемой пары (i =2,…, k).
Блок-схема алгоритма представлена на рис.6.

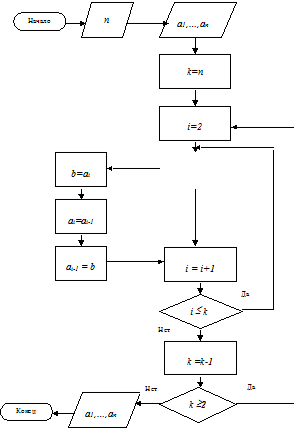
Рис. 6. Блок-схема алгоритма сортировки, метод «Пузырек».
Пример 9. Написать блок-схему алгоритма произведения двух матриц (пример алгоритма с тройным циклом).
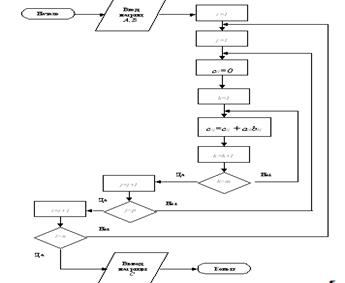
Рис. 7. Блок-схема алгоритма перемножения двух матриц
Напомним, что перемножать можно матрицы, у которых количество столбцов первой матрицы равно количеству строк второй матрицы. Пусть имеется матрица А, размера n x m и матрица В, размера m x p. Тогда произведением этих матриц будет матрица С=АВ, элементы которой определяются по формуле:
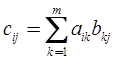 (3)
(3)
Формировать матрицу С будем по строкам. Вначале организуем цикл перебора строк. Внутри этого цикла будем перебирать столбцы. Внутри этих циклов организуем цикл накопления суммы произведений элементов i –й строки матрицы А, на элементы j-го столбца матрицы В.
Контрольные вопросы
1. Что подразумевается под выражением: составить алгоритм решения задачи?
2. Важно ли понятие исполнителя при формулировании алгоритма?
3. Опишите свойства алгоритмов.
4. Что подразумевается под определенностью алгоритма?
5. Представляют ли ценность алгоритмы не обладающие свойством массовости? Почему?
6. Какие бывают виды алгоритмов?
7. Дайте определение оператора и опишите структурную классификацию операторов.
8. Опишите классификацию операторов по назначению.
9. Какие Вы знаете операторы цикла?
10. Опишите правила передачи управления внутрь цикла и из цикла.
11. Что такое операторная схема алгоритма?
12. Что такое блок-схема алгоритма?
13. Опишите основные конструкции, применяемые при составлении блок-схем алгоритмов.
14. Опишите структуры операторов цикла с предусловием и постусловием.
15. Какая структура обеспечивает в алгоритме ветвление по нескольким направлениям?
16. Какие методы конструирования алгоритмов Вы знаете?
17. Что такое последовательная декомпозиция алгоритма?
Контрольные задания
Задание 1
1. Дайте определение понятий «информация» и «экономическая информация».
2. Перевести два числа в двоичную систему счисления и найти их двоичную сумму:
145,875; 1581,5
3. Составить алгоритмы решения следующих задач:
1. Напечатать таблицу перевода температуры из градусов по шкале Цельсия (С) в градусы шкалы Фаренгейта (F) для значений от 15°С до 30°С с шагом 1°С. (Перевод осуществляется по формуле F=l,8C+32.)
2. В области 10 районов. Известны площади, засеваемые пшеницей, и средняя урожайность (ц/га) в каждом районе. Определить количество пшеницы, собранное в области, и среднюю урожайность по области.
Задание
1. Дайте определение информационных единиц: реквизита, документа.
2. Перевести два числа в шестнадцатеричную систему счисления и найти их шестнадцатеричную сумму:
4096; 1581,5
3. Составить алгоритмы решения следующих задач:
1. Напечатать таблицу соответствия между весом в фунтах и весом в кг для значений от 1 до 10 фунтов с шагом 1 фунт (1 фунт =400г).
2. Задан алфавитный список участников соревнований по плаванию и их результаты. Напечатать фамилии по убыванию результатов.
Задание 3
1. Какие основные операции выполняются над признаками и основаниями при обработке экономической информации?
2. Выполнить операцию умножения над двумя двоичными числами:
100011,1(2); 1101,01(2)
3. Составить алгоритмы решения следующих задач:
1.Дана ведомость результатов сдачи экзаменов по трем предметам в группе, состоящей из 25 студентов. Напечатать отличников.
2.Составить алгоритм, в котором определяется наименьший элемент матрицы А( n , m ), а затем его значение вычитается из всех элементов этой матрицы.
Задание 4
1. Дайте определение составных единиц информации: показателя, массива.
2. Перевести числа в десятичную систему:
1000111,01(2); 1675, 4(8)
3. Составить алгоритмы решения следующих задач:
1. Вычислить приближенно площадь одной арки синусоиды, разделив отрезок от 0 до на 1 частей и суммируя площади десяти прямоугольников с основанием 1 и высотой, равной значению функции на правой границе каждого интервала.
2. Составить алгоритм определения сумм элементов столбцов матрицы А( n , m ).
Задание 5
1. В чем суть электронной информационной технологии решения задач?
2. Найти разность двух двоичных чисел:
10000100,1(2); 1011101,01(2).
3. Составить алгоритмы решения следующих задач:
1. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый следующий день он увеличивал дневную норму на 10 % от нормы предыдущего дня. Какой суммарный путь пробежит спортсмен за 7 дней?
2. Пусть имеется ряд наблюдений х1,х2,…,х n. Составить алгоритм для нахождения цепных приростов, цепных темпов роста, среднего прироста, среднего темпа роста.
Задание 6
1. Что является теоретической основой компьютерной информатики?
2. Перевести два числа в шестнадцатеричную систему счисления и найти их двоичную сумму:
145,875; 1581,5
3. Составить алгоритмы решения следующих задач:
1. Информация о количестве осадков выпадавших в течение месяца, и о температуре воздуха задана в виде двух массивов. Определить, какое количество осадков выпало в виде дождя, какое в виде снега. (Считать, что идет дождь, если температура воздуха >0°С).
2. Составить алгоритм определения наибольшего элемента матрицы А(n,m) с указанием его номера строки и столбца.
Задание 7
1. Что понимается под информационной моделью задачи?
2. Перевести два числа в шестнадцатеричную систему счисления и найти их шестнадцатеричную сумму:
2096; 681,5
3. Составить алгоритмы решения следующих задач:
1. Одноклеточная амеба каждые 3 часа делится на 2 клетки. Определить сколько клеток будет через 3, 6, 9, 12, ..., 24 часа.
2. Рост учеников класса представлен в виде массива. Рост девочек кодируется знаком “+”, рост мальчиков знаком “-”. Определить средний рост мальчиков.
Задание 8
1. Опишите основные конструкции, применяемые при составлении блок-схем алгоритмов.
2. Выполнить операцию умножения над двумя двоичными числами:
1101011,1(2); 101101,101(2)
3. Составить алгоритмы решения следующих задач:
1. В ЭВМ поступают результаты соревнований по плаванию для трех спортсменов. Выбрать и напечатать лучший результат. Решить задачу для следующих наборов данных: 1) 11,3; 10,6; 11; 2) 10; 10,9; 13; 3) 16; 18; 13.
2. Составить алгоритм определения наименьшего элемента матрицы А(n,m) с указанием его номера строки и столбца.
Задание 9
1. На какие части делится программное обеспечение для персонального компьютера?
2. Перевести числа в десятичную систему:
1А1F,1(16); 34075, 4(8)
3. Составить алгоритмы решения следующих задач:
1. Вводя в цикле по 4 оценки, полученные студентами и сессию, определить число неуспевающих студентов и средний балл группы по всем экзаменам.
2. Заданы две выборки х1,х2,…,х n ; у1,у2,…,у n . Составить алгоритм определения выборочного коэффициента корреляции
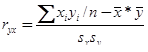 ,
,
где: 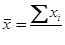 - среднее значение наблюдений первой выборки;
- среднее значение наблюдений первой выборки;
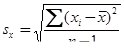 - несмещенное среднее квадратичное отклонение наблюдений первой выборки. Аналогично и для второй выборки.
- несмещенное среднее квадратичное отклонение наблюдений первой выборки. Аналогично и для второй выборки.
Задание 10
1. Что такое системное программное обеспечение? Какое программное обеспечение оно включает?
2. Доказать общезначимость формулы:
AÙ(AÞB)ÞB
3. Составить алгоритмы решения следующих задач:
1. В области 10 районов. Заданы площади, засеваемые в каждом районе пшеницей, и урожай, собранный в каждом районе. Определить среднюю урожайность пшеницы по каждому району и по области в целом.
2. Изменение основных фондов отрасли описывается разностным уравнением:
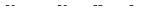 .
.
Задан план инвестиций I 0 , I 1 ,…, In и начальное значение основных фондов К1. Составить алгоритм для определения значений К2,…,К n, а также нахождения цепных приростов, цепных темпов роста основных фондов.
Задание 11
1. Что такое система программирования?
2. Перевести два числа в двоичную систему счисления и найти их двоичную сумму:
1045,075; 1634,25
3. Составить алгоритмы решения следующих задач:
1. Определить, сколько различных сигналов может быть подано m флажками различных цветов. Отличие сигналов заключается в порядке расположения разноцветных флажков на мачте. Решить при m=6.
2. Пусть имеется ряд наблюдений х1,х2,…,х n. Составить алгоритм определения среднего значения хср и среднего квадратичного отклонения sx по формулам:
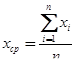 ;
; 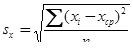
Задание 12
1. Какие классы наиболее распространенного прикладного программного обеспечения вы знаете?
2. Показать, что формула является тавтологией:
ØAÙ(AÚB)ÞB.
3. Составить алгоритмы решения следующих задач:
1. В ЭВМ по очереди поступают результаты соревнования по плаванию, в которых участвует п спортсменов. Выдавать на печать лучший результат после ввода результата очередного спортсмена.
2. Составить алгоритм определения будущего значения накопленного капитала по известной процентной ставке р%, начальному вкладу А0 и известным периодическим платежам bi ,( i =0,1,…, n -1). Ai+1=p(Ai+bi).
Задание 13
14. Изобразите структурную схему персонального компьютера.
15. Выполнить операцию умножения над двумя двоичными числами:
1001,0101(2); 10111,1101(2)
3. Составить алгоритмы решения следующих задач:
1. Около стены наклонно стоит палка длиной x. Один ее конец находится на расстоянии y от стены. Определить значение угла между палкой и полом для значений x = 4,5 м и y , изменяющегося от 2 до 3 м с шагом 0,2 м.
2. Составить программу для обработки результатов кросса на 500 м для женщин. В кроссе участвует не более 100 студенток. Для каждой участницы внести фамилию, шифр группы, фамилию преподавателя, результат. Получить результирующую таблицу, упорядоченную по результатам, в которой содержится также информация о выполнении нормы 1 разряда. Определить суммарное количество студенток, выполнивших эту норму.
Задание 14
1. Каким является типовое устройство микропроцессора (модель)?
2. Перевести числа в десятичную систему:
B0345(16); 4625,14(8)
3. Составить алгоритмы решения следующих задач:
1. Задано п троек чисел а, Ь, с. Вводя их по очереди и интерпретируя как длины сторон треугольника, определить, сколько троек может быть использовано для построения треугольника (числа а, b , с при вводе расположить в порядке возрастания).
2. Для формирования сборной страны по хоккею предварительно выбрано 30 игроков. На основании протоколов игр (всего 10 игр) составлена таблица, в которой содержится штрафное время каждого игрока по каждой игре (штрафное время может составлять 2, 5 или 10 мин). Составить программу, которая составляет предварительный список кандидатов в сборную и определяет для каждого из них суммарное и штрафное время. Игроки, оштрафованные хотя бы один раз на 10 мин, из кандидатов в сборную исключаются.
Задание 15
1. Какие типы микропроцессоров применяются на персональном компьютере?
2. Найти разность двух восьмеричных чисел:
120405,6(8); 17526,71(8).
3. Составить алгоритмы решения следующих задач:
1. Написать программу, которая спрашивала бы сокращенное имя, а печатала полное (например, Саша - Александр) для пяти ваших друзей. Ввод незнакомого имени должен провоцировать заявление типа: “Я с Вами не знакома”. Необходимые данные задать самостоятельно.
2. Сформировать из матрицы А(10,10) матрицу В(10,10) по следующим правилам:
а) элементы матриц А и В принимают только значения 0 или 1;
б) соседями элемента аij считаются все элементы, расположенные рядом с данным по горизонтали, вертикали или диагонали;
в) если сумма S значений соседей элемента aij меньше двух или больше трех, то bij=0;
г) если сумма S значений соседей равна двум, то bij=аij;
д) если сумма S значений соседей равна трем, то bij=1.
По окончании формирования матрицы В значения элементов построчно вывести на печать, заменяя 0 - символом “ “; 1 - символом *.
Задание 16
1. Что такое регистр? Приведите примеры регистров микропроцессора.
2. Пользуясь таблицей истинности доказать тавтологию:
(AÞB)Ù(BÞC)Þ(AÞC)
3. Составить алгоритмы решения следующих задач:
1. Составить программу, реализующую эпизод сказки: спрашивает, куда предпочитает пойти герой (налево, направо или прямо), и печатает, что его ждет в каждом случае. Ответ ЭВМ присвоить символьной переменной и напечатать. Текст вопросов и ответов ЭВМ задать самостоятельно.
2. В соревнованиях участвуют три команды по 6 человек. Результаты соревнований в виде мест участников каждой команды (1-18) размещены в трех массивах, содержащих по 6 компонент. Определить команду - победителя, вычислив количество баллов, набранное каждой командой. Участнику, занявшему 1-е место, начисляется 5 баллов, 2-е - 4, 3-е - 3, 4-е - 2, 5-е - 1, остальным - 0 баллов.
Задание 17
1. Какие типы памяти Вы знаете?
2. Перевести два числа в шестнадцатеричную систему счисления и найти их шестнадцатеричную сумму:
3025; 4612,25
3. Составить алгоритмы решения следующих задач:
1. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый следующий день он увеличивал дневную норму на 10 % от нормы предыдущего дня. Через сколько дней спортсмен пробежит суммарный путь 150 км?
2. Известно, что и Москве самыми теплыми являются дни с 15 июля по 15 августа. Для проведения фестиваля были выбраны 7 следующих подряд дней, наиболее теплых по данным за последние 10 лет. Составить программу для выполнения этой работы на ЭВМ.
Задание 18
1. Что представляет собой кэш-память?
2. Выполнить операцию умножения над двумя двоичными числами:
110101,01(2); 10111,11(2)
3. Составить алгоритмы решения следующих задач:
1. Составить программу для определения подходящего возраста кандидатуры для вступления в брак, используя следующее соображение: возраст девушки равен половине возраста мужчины плюс 7, возраст мужчины определяется соответственно как удвоенный возраст девушки минус 14. Данные для проверки работы программы задать самостоятельно.
2. Японская радиокомпания провела опрос 250 радиослушателей по вопросу: “Какое животное Вы связываете с Японией и японцами?”. Составить программу получения пяти наиболее часто встречающихся ответов и их долей (в %).
Задание 19
1. Что такое контроллер, какие типы контроллеров бывают?
2. Пользуясь законами эквивалентности упростить:
XÚ(YÚX)ÚY
3. Составить алгоритмы решения следующих задач:
1. В киоске продается газета стоимостью 70 коп. и журнал стоимостью 1 грн. 20 коп. Составить программу, которая спрашивает о желании покупателя (журнал или газета?), принимает деньги (сумма денег вводится с клавиатуры) и печатает причитающуюся сдачу. Исходные данные задать самостоятельно.
2. Составить программу для ведения протокола баскетбольной игры. Во время игры машина ведет учет набранных очков и фолов каждого игрока. Игрок, получивший 5 фолов, удаляется из игры (эта информация должна появляться на экране). В конце игры должна выводиться информация о сумме очков, набранных каждым игроком, в порядке убывания.
Задание 20
1. Какие внешние устройства компьютера Вы знаете?
2. Найти разность двух двоичных чисел:
11010000,01(2); 1011101,11(2).
3. Составить алгоритмы решения следующих задач:
1. Вводя в цикле по 5 оценок каждого студента, получить число студентов, не имеющих оценок 2 и 3. В группе учится п, студентов.
2. Результаты переписи населения хранятся в памяти ЭВМ. Используя массивы фамилий и года рождения, напечатать фамилии и подсчитать общее число жителей, родившихся раньше 1928 года.
Задание 21
1. Что такое системная магистраль и какие основные магистрали данных используются в персональном компьютере?
3. Пользуясь законами эквивалентности упростить:
(XÚY)Ù(XÚØY)
3. Составить алгоритмы решения следующих задач:
1. В 1995 году урожай ячменя составил 20ц с га. В среднем каждые 2 года за счет применения передовых агротехнических приемов урожай увеличивается на 5 %. Определить, через сколько лет урожайность достигнет 25ц с га.
2. Результаты соревнований фигуристов по одному из видов многоборья представлены оценками судей в баллах (от 0 до 6). По результатам оценок судьи определяется место каждого участника у этого судьи. Места участников определяются далее по сумме мест, которые каждый участник занял у всех судей. Составить программу, определяющую по исходной таблице оценок фамилии и сумму мест участников в порядке занятых ими мест. Число участников не более 15, число судей не более 10.
Задание 22
1. Системный блок компьютера, что он включает?
2. Перевести два числа в шестнадцатеричную систему счисления и найти их шестнадцатеричную сумму:
1034; 2032,5
3. Составить алгоритмы решения следующих задач:
1. Определить средний рост девочек и мальчиков одного класса. В классе учится п учеников.
2. В памяти ЭВМ хранятся списки номеров телефонов и фамилий абонентов, упорядоченные по номерам телефонов, для каждого из пяти телефонных узлов города. Один телефонный узел включает несколько АТС (не более 10), Номера АТС (первые две цифры номера телефона), относящихся к каждому телефонному узлу, также хранятся в памяти ЭВМ. Составить программу, обеспечивающую быстрый поиск фамилии абонента по заданному номеру телефона.
Задание 23
1. Опишите свойства алгоритмов.
4. Пользуясь законами эквивалентности упростить:
ØXÞ(XÙY)
3. Составить алгоритмы решения следующих задач:
1. Определить суммарный объем в литрах 12 вложенных друг в друга шаров со стенками 5 мм. Внутренний диаметр внутреннего шара равен 10 см. Считать, что шары вкладываются друг в друга без зазоров.
2. При выборе места строительства жилого комплекса при металлургическом заводе необходимо учитывать “розу ветров” в данной местности. На основании данных ежедневного определения направления ветра, проводимого в течение года, определить целесообразное взаимное расположение промышленной и жилой зоны.
Указание. Направление ветра кодируется следующим образом:1 – северный; 2 – южный; 3 – восточный; 4 – западный; 5 - северо-западный;
6 - северо-восточный; 7 - юго-западный; 8 - юго-восточный
Задание 24
1. Дайте определение оператора и опишите структурную классификацию операторов.
2. Перевести числа в десятичную систему:
1010101,0111(2); 10705,014(8)
3. Составить алгоритмы решения следующих задач:
1. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый следующий день он увеличивал дневную норму на 10 % от нормы предыдущего дня. Через сколько дней спортсмен будет пробегать в день больше 20 км?
2. Составить результирующую таблицу первенства по футболу, в котором участвуют 10 команд. В качестве исходной информации задан счет: количество забитых (пропущенных) мячей в каждой проведенной игре. Для получения итогового результата необходимо по заданной таблице забитых (пропущенных) мячей составить таблицу очков (выигрыш - 3, ничья - 1, проигрыш - 0). Далее определить сумму очков для каждой команды и в соответствии с этим распределить команды по местам. Если сумма очков у двух команд одинакова, то сравниваются разности забитых и пропущенных мячей.
Задание 25
1. Что такое блок-схема алгоритма?
2. Записать логическое выражение, которое принимает значение истина, если точка с координатами (x,y) попадает в заштрихованную область. На рисунке окружности имеют радиусы: большая – 9, меньшая – 5, центр первой имеет координаты (1,4), а второй – (-2,0). Прямая пересекает ось ОХ в точке (11,0), а ось ОУ в точке (0,9).
3. Составить алгоритмы решения следующих задач:
а) Составить таблицу стоимости порций сыра весом 50, 100, 150, ..., 1000 грамм (цена 1 кг 15 грн.).
б) Фамилии участников соревнований по фигурному катанию после короткой программы расположены в порядке, соответствующем занятому месту. Составить список участников в порядке их стартовых номеров для произвольной программы (участники выступают в порядке, обратном занятым местам).
[1] Годичное Общее собрание Академии наук СССР //Вестн. АН СССР, 1983. №6. с.3-60.
[2] А.П. Ершов. Информатика: предмет и понятие. // В сб. Кибернетика. Становление информатики. – М.: Наука, 1986. -192с.
[3] Экономическая информатика, /Под ред. П.В. Конюховского и Д.Н. Колесова. –СПб:Питер, 2000. -560с.
[4] Дибкова Л.М. Інформатика та комп’ютерна техніка: Посібник для студентів вищих навчальних закладів. –К.: Видав. Центр «Академія», 2002. -320с (Альма-матер).
[5]Інформатика: Комп’ютерна техніка. Комп’ютерні технології: Підручник /За ред.. О. І. Пушкаря. –К.: Вид. центр «Академія», 2002. -704с. (Альма-матер).
[6] В.С. Михалевич, Ю.М. Каныгин, В.И. Гриценко Информатика –новая область науки и практики. // В сб. Кибернетика. Становление информатики. –М.: Наука, 1986. -192с.
[7] А.П. Ершов Информатика: Предмет и понятие. // В сб. Кибернетика. Становление информатики. – М.: Наука, 1986. -192с.
[8] А.А. Дородницын Информатика: Предмет и задачи. . // В сб. Кибернетика. Становление информатики. – М.: Наука, 1986. -192с.
Дата: 2019-07-30, просмотров: 588.