В математических и других рассуждениях постоянно встречаются повествовательные предложения, образованные путем видоизменения некоторого предложения с помощью слова не или связывания предложений с помощью слов и, или, если …, то (или влечет), тогда и только тогда, когда. Эти пять слов или комбинаций слов называются сентенциональными связками. Они являются основой для построения сложных предложений (т.е. таких повествовательных предложений в которых содержится одна или более чем одна связка), составленных их простых предложений (т.е. таких, каждое из которых или не содержит связку, или рассматривается как «неразложимое»).
Повествовательное предложение о котором можно сказать истинно оно или ложно мы будем называть высказыванием. Множество повествовательных предложений и сентенциональных связок образует исчисление высказываний. Если обозначать высказывания большими латинскими буквами и ввести для сентенциональных связок условные обозначения (значки), то можно перейти к логическим формулам результатом которых будут логические значения – истина или ложь.
Дадим определения для основных логических операций.
1. Конъюнкцией (или операцией логического умножения) двух высказываний A и B называют высказывание C, которое истинно тогда и только тогда, когда истины оба высказывания входящие в конъюнкцию. Конъюнкция (иногда логическое «и») обозначается значком  и записывается так: A
и записывается так: A  B.
B.
2. Дизъюнкцией (или операцией логического сложения) двух высказываний A и B называют высказывание C, которое ложно тогда и только тогда, когда ложны оба высказывания входящие в дизъюнкцию. Дизъюнкция (иногда логическое «или») обозначается значком Ú и записывается так: AÚB.
3. Отрицанием высказывания A называют высказывание B которое ложно тогда и только тогда когда истинно исходное высказывание A, обозначают 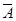 (иногда ØA).
(иногда ØA).
4. Импликация высказываний (или условное предложение) обозначается AÞB и задается с помощью следующей таблицы, называемой таблицей истинности для импликации:
| A | B | AÞB |
| Истина | Истина | Истина |
| Истина | Ложь | Ложь |
| Ложь | Истина | Истина |
| Ложь | Ложь | Истина |
4. Эквиваленция или эквивалентность двух высказываний обозначается AÛB и задается следующей таблицей истинности:
| A | B | AÛB |
| Истина | Истина | Истина |
| Истина | Ложь | Ложь |
| Ложь | Истина | Ложь |
| Ложь | Ложь | Истина |

 Среди всех сложных высказываний или логических формул наибольший интерес представляют такие, которые принимают значение истина при любых истинностных значениях входящих в них логических переменных (высказываний). Они называются тождественно истинными высказываниями или тавтологиями, обозначаются значком . Для доказательства общезначимости логических формул (того, что формула есть тавтология) пользуются таблицами истинности или применяют основные законы эквивалентности математической логики, которые также доказываются применением таблиц истинности.
Среди всех сложных высказываний или логических формул наибольший интерес представляют такие, которые принимают значение истина при любых истинностных значениях входящих в них логических переменных (высказываний). Они называются тождественно истинными высказываниями или тавтологиями, обозначаются значком . Для доказательства общезначимости логических формул (того, что формула есть тавтология) пользуются таблицами истинности или применяют основные законы эквивалентности математической логики, которые также доказываются применением таблиц истинности.
Законы эквивалентности
1. Законы коммутативности (они позволяют переставлять операнды Ù,Ú и Û):
(AÙB)Û(BÙA)
(AÚB)Û(BÚA)
(AÛB)Û(BÛA)
2. Законы ассоциативности (они позволяют нам пренебрегать скобками):
(AÙB) ÙС Û A Ù(BÙC)
(AÚB) ÚС Û A Ú(BÚC)
3. Законы дистрибутивности (они позволяют раскрывать скобки):
AÚ(B ÙС) Û (A ÚB)Ù(AÚC)
AÙ(B ÚС) Û (A ÙB)Ú(AÙC)
4. Законы де Моргана:
Ø(AÙB) Û ØAÚØB
Ø(AÚB) Û ØAÙØB
5. Закон отрицания: Ø(ØA) Û A
6. Закон исключенного третьего: AÚØA Û истина
7. Закон противоречия: AÙØA Û ложь
8. Закон импликации: (AÞB)Û( ØAÚB)
9. Закон равенства: (AÛB) Û (AÞB)Ù(BÞA)
10. Законы упрощения Ú:
AÚA Û A
AÚИстина ÛИстина
AÚЛожьÛА
АÚ(АÙВ)ÛА.
11. Законы упрощения Ù:
АÙАÛА
АÙИстинаÛА
АÙЛожьÛЛожь
АÙ(АÚВ)ÛА
12. Закон тождества:
АÛА.
Операции математической логики имеют свое старшинство, т.е. порядок их выполнения: 1) Ø, 2) Ù, 3) Ú, 4) Þ, 5) Û.
 Пример 1. Доказать общезначимость формулы:
Пример 1. Доказать общезначимость формулы:
(АÛВ)Ù(ВÛС)Þ(АÛС)
Для доказательства воспользуемся таблицей истинности. Заметим, что количество строк в такой таблице равно 8 (2n – где, n – количество логических переменных).
Будем в таблице истину обозначать – и, а ложь – л.
| А | В | С | АÛВ | ВÛС | (АÛВ)Ù(ВÛС) | АÛС | Вся формула |
| и | и | и | и | и | и | и | и |
| и | и | л | и | л | л | л | и |
| и | л | и | л | л | л | и | и |
| л | и | и | л | и | л | л | и |
| и | л | л | л | и | л | л | и |
| л | и | л | л | л | л | и | и |
| л | л | и | и | л | л | л | и |
| л | л | л | и | и | и | и | и |
Пример 2. Используя основные законы эквивалентности доказать эквивалентность формул U и V, когда
| U = XÞ(XÙY)Þ((XÞY)ÞY)ÞZ |
| V = YÞ(XÞZ) |
Применяя основные законы эквивалентности к каждой формуле в отдельности покажем, что они дают одно и то же логическое выражение (формулу). Далее, на основании равенства правых частей сделаем заключение о равенстве левых.
Рассмотрим V:
| V = YÞ(XÞZ) |
| ØYÚ(ØXÚZ) |
| ØYÚØXÚZ |
Рассмотрим U:
| U = XÞ(XÙY)Þ((XÞY)ÞY)ÞZ |
| ØXÚ(ØXÚØYÚ((Ø(ØXÚØY)ÚY)ÙZ)) |
| ØXÚØXÚØYÚ(((XÙØY)ÚY)ÙZ) |
| ØXÚØYÚ(((XÚY)Ù(ØYÚY)ÙZ) |
| ØXÚØYÚ((XÚY)Ù Z) |
| ØXÚØYÚ((XÙZ)Ú(YÙZ)) |
| ØXÚØYÚ(XÙZ)Ú(YÙZ) |
| (ØXÚ(XÙZ))Ú(ØYÚ(YÙZ)) |
| ((ØXÚX)Ù(ØXÚZ))Ú((ØYÚY)Ù(ØYÚZ)) |
| (ØXÚZ)Ú(ØYÚZ) |
| ØXÚZÚØYÚZ |
| ØXÚØYÚZ |
Тем самым эквивалентность доказана.
Пример 3. Записать логическое выражение принимающее значение истина в случае когда точка с координатами (x,y) находится внутри заштрихованной области. На рисунке даны окружность с единичным радиусом и парабола у=х2.
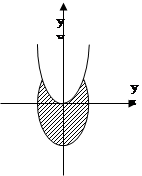 |
Рис.1. - Окружность с единичным радиусом
Выражение имеет следующий вид: (X2+Y2£1)Ù(Y£X2).
Пример 4. Записать логическое выражение, принимающее значение истина в случае когда точка с координатами (x,y) находится внутри заштрихованной области. На рисунке даны окружность с единичным радиусом и парабола у=х2.
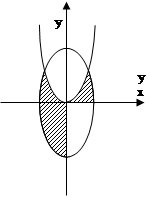 |
Рис.2. - Окружность с единичным радиусом
Выражение имеет следующий вид:
((X£0)Ù(X2+Y2£1)Ù(Y£X2))Ú((X2+Y2£1)Ù(Y£X2)Ù(Y³0)).
Контрольные вопросы
1. Что такое сентенциональные связки?
2. Дайте определение высказывания.
3. Как определяются основные логические операции?
4. Что значит общезначимость логической формулы?
5. Выпишите основные законы эквивалентности.
6. Какие приоритеты имеют логические операции?
7. Пользуясь основными законами эквивалентности доказать общезначимость формулы:
(AÞB)Þ((BÞC)Þ(AÞC)).
Используя таблицу истинности доказать следующий закон эквивалентности:
(AÞB)Û( ØAÚB).
8. Записать логическое выражение принимающее значение истина в случае когда точка с координатами (x,y) находится внутри заштрихованной области.
Структурная схема ЭВМ
Общая структурная схема персонального компьютера представлена на рис. 1. Для простоты на этой схеме показано лишь одно устройство ввода и одно устройство вывода. Основная память компьютера состоит из двух частей – оперативного запоминающего устройства (ОЗУ) и постоянного запоминающего устройства (ПЗУ).
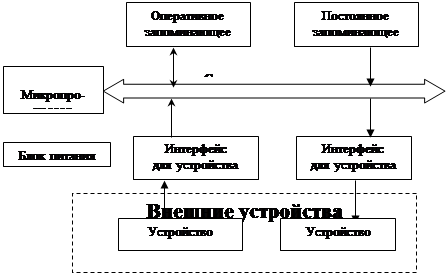 |
Рис. 1. Общая структурная схема персонального компьютера.
Микропроцессор является главным компонентом компьютера. Характеристики микропроцессора – длина разрядной сетки (или разрядность слова), набор выполняемых команд, быстродействие и другие – в основном определяют характеристики компьютера. Микропроцессор выполняет следующие функции: управление и координация работы всех других компонентов компьютера; выборка команд и обрабатываемых данных из основной памяти; декодирование команд; выполнение с помощью арифметического устройства арифметических, логических и других операций, закодированных в командах; передача данных между микропроцессором и основной памятью, а также между микропроцессором и устройствами ввода-вывода; обработка сигналов от устройств ввода-вывода, в том числе обработка сигналов прерывания с этих устройств.
Микропроцессор – сложное цифровое электронное устройство. К основным элементам, влияющим на временные характеристики выполнения программ, относятся: форматы и системы команд микропроцессора; длительность выполнения разных команд; имена (или номера) программно-доступных регистров (так называются регистры, которые могут использоваться в составляемых программах); длина разрядной сетки (разрядность); правила адресации внешних устройств и особенности выполнения операций ввода-вывода; размер адресного пространства; схема обработки прерываний.
Перечисленные элементы образуют основу архитектуры микропроцессора и в совокупности представляют собой модель микропроцессора. Для разных типов микропроцессоров существует своя модель.
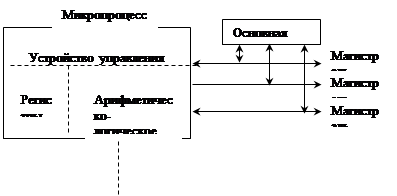 |
Рис. 2. Микропроцессор и его связи с основной памятью.
В состав микропроцессора входят: устройство управления (УУ), арифметическо-логическое устройство (АЛУ) и набор регистров.
Устройство управления предназначено для управления работой всех компонентов микропроцессора и обеспечения должного взаимодействия различных компонентов друг с другом. Управление осуществляется с помощью импульсных сигналов, посылаемых УУ на соответствующие входы управляемых компонентов. Кроме того, УУ может получить ответные сигналы с управляемых компонентов.
Физически УУ представляет собой цифровую электронную схему, на вход которой поступают коды подлежащих выполнению операций, а выходом являются серии импульсных управляющих сигналов. Таким образом, восприняв код той или иной операции, УУ формирует цепочку управляющих сигналов и подает их в нужные точки микрокомпьютера.
Число выходов УУ, по которым выдаются управляющие сигналы, обычно довольно велико. Например, УУ, показанное на рис. 3, имеет 16 выходов.

Рис.3. Устройство управления микропроцессора.
Надо иметь в виду, что импульсные сигналы на выходах в общем случае появляются не одновременно, а со сдвигом во времени. Так, УУ на рис.3 может выдать импульс сначала на выходе 3, затем на выходе 1, следом – одновременно на выходах 2 и 5, потом на выходе 4 и т.д. После выдачи последнего импульса в данной цепочке управляющих сигналов текущая операция считается законченной, и вслед за этим на вход УУ может быть подан код новой операции.
Арифметико-логическое устройство предназначено для исполнения арифметических и логических операций. Основу АЛУ составляет операционный блок – цифровое электрическое устройство, которое может настраиваться на различные операции и непосредственно осуществлять их. Настройка операционного блока на конкретную операцию и последовательность шагов ее выполнения обеспечивается с помощью управляющих сигналов УУ.
Регистры являются важными элементами микропроцессора. Регистр – это электронное цифровое устройство для временного запоминания информации в форме двоичного числа, или кода. Запоминающим элементом в регистре является триггер, который может находиться в одном из двух состояний. Одно из этих состояний соответствует запоминанию двоичного нуля, другое – запоминанию двоичной единицы. В общем случае регистр содержит несколько связанных друг с другом триггеров – по одному триггеру на каждый запоминаемый разряд двоичного числа. Число триггеров в регистре называется разрядностью регистра. Например, регистр из восьми триггеров – это 8-разрядный, или 8-битовый, регистр (так как каждый разряд регистра обеспечивает хранение одного бита информации).
Регистры, используемые не только для хранения информации, но и для ее преобразования, называются управляемыми. Например, управляемый регистр может осуществлять замену всех хранящихся в нем двоичных единиц нулями, а нулей – единицами (операция инвертирования кода), прибавление единицы к числу, хранящемуся в регистре, вычитание единицы и т.п. Операции над числом в регистре реализуются с помощью управляющих сигналов от УУ.
Многие регистры специализированны по своей функции. Так существует регистр-аккумулятор, или просто аккумулятор, программный счетчик, регистр команд, регистр адреса памяти и т.д. Аккумулятор входит в АЛУ и предназначен для хранения одного из операндов перед выполнением операции в АЛУ или для кратковременного запоминания результата операции. Операнд – это данное, используемое в текущей операции. Например, в операции суммирования операндами являются оба слагаемых.
Программный счетчик (счетчик команд, регистр адреса команды) служит для формирования и запоминания адреса очередной выполняемой команды. После выполнения каждой команды программный счетчик содержит адрес следующей команды, по которому эта команда хранится в памяти компьютера.
Регистр команд используется для хранения кода текущей выполняемой команды. Входящий в состав команды код операции используется, как уже говорилось, для формирования в УУ определенной серии управляющих сигналов, зависящей от конкретного кода операции. Оставшаяся часть кода команды может содержать информацию об адресах операндов, участвующих в выполнении данной команды.
Регистр адреса памяти служит для запоминания адреса команды, операнда или результата операций в память. Регистр адреса памяти может входить не в состав микропроцессора, а в состав элементов памяти компьютера.
Изменить роль специализированных регистров или даже узнать их содержимое программным путем нельзя, т.е. эти регистры, как говорят, программно-недоступны. Но в состав микропроцессора входят и регистры, которые программист может использовать в своей программе. Такие регистры микропроцессора называют программно-доступными. Состав и назначение их различны в разных типах микропроцессоров. Однако среди них почти всегда имеется регистр слова состояния процессора (РССП) и несколько регистров общего назначения (РОН).
Регистр слова состояния процессора хранит слово состояния процессора (ССП), отражающее информацию о состоянии микропроцессора и выполняемой им программы в каждый данный момент времени. В частности, в РССП обычно запоминаются признаки результата выполнения команды (отрицательного результата, переполнения разрядной сетки и т.п.). Таким образом, хотя РССП и предназначен для особых функций, он программно-доступен, т.е. с помощью соответствующих команд, заложенных в программу, можно читать и даже частично изменять его содержимое.
Регистры общего назначения обычно не имеют конкретного функционального назначения. Программист может в своей программе задействовать их так, как он считает нужным. Например, результат выполнения некоторой команды можно не посылать в основную память, а временно запомнить в каком-нибудь РОНе с тем, чтобы позднее, в другой команде, использовать этот результат. Чтобы отличить РОНы друг от друга, им присвоены уникальные имена (или номера), которые и записываются в программе. Существуют микропроцессоры, в которых РОНы применяются и для специальных целей. Например, один из РОНов может выполнять функции программного счетчика, или счетчика команд, хранящего в каждый момент времени адрес очередной команды программы, другой – функции указателя стека, необходимого при обработке прерываний и т.д.
На персональных компьютерах используются микропроцессоры фирмы Intel, а также совместимые с ними фирм AMD, Cyrix, IBM. Исторически на IBM PC-совместимых компьютерах применялись и применяются следующие микропроцессоры: Intel-8088, 80286, 80386 (модификации SX и DX), 80486 (модификации SX, SX2, DX, DX2, DX4), Pentium, Pentium Pro, Pentium II (и его модификации Celeron и т.д.). Основная память. Основная память – важнейший компонент персонального компьютера. Название «основная» отличает эту память от внешней памяти, которая организуется на некотором внешнем устройстве (например, на НГМД). Это название говорит о том, что микропроцессор может обрабатывать только те данные, которые хранятся в основной памяти. Основная память обычно состоит из двух частей – ОЗУ и ПЗУ.
Оперативное запоминающее устройство (ОЗУ) обеспечивает чтение находящихся в нем данных и запись в него новых данных. В компьютерах ОЗУ обычно реализуется как энергозависимая память, т.е. такая память, содержимое которой разрушается («стирается») при выключении питания компьютера. Часто для обозначения оперативной памяти используют аббревиатуру RAM (random access memory), т.е. память с произвольным доступом. Микросхемы ОЗУ собираются в блоки различной емкости. Наиболее распространены емкости 16, 32, 64 и 128 мегабайт. В зависимости от способа работы микросхем памяти они бывают SIMM или DIM, последние наиболее распространены. Для убыстрения доступа к оперативной памяти на быстродействующих компьютерах используется еще и дополнительная специальная сверхбыстродействующая память, так называемая кэш-память. Она хранит копии наиболее часто используемых участков оперативной памяти и как бы занимает промежуточное положение между микропроцессором и оперативной памятью. Кэш-память может располагаться или внутри микропроцессора, или в виде отдельной платы. Так микропроцессоры серий 486 и Pentium содержат небольшую внутреннюю кэш-память. Часто кэш-память, располагаемую отдельно от микропроцессора называют кэш-памятью второго уровня (level two cache, L2 cache). В микропроцессоре Pentium Pro,например, кэш-память второго уровня содержится в едином с ним корпусе. Микропроцессоры 486 серии и Pentium обычно оснащаются кэш-памятью емкостью 256 Кбайт.
Постоянное запоминающее устройство (ПЗУ) обеспечивает только чтение данных, которые однажды были записаны в ПЗУ. Таким образом, содержимое ПЗУ не может быть изменено компьютером, оно постоянно (отсюда и название вида памяти). Это устройство создается как энергозависимая память: ее содержимое не «стирается» при выключении питания компьютера. Запись нужных данных в ПЗУ осуществляется на специальных устройствах, вне компьютера. В ПЗУ обычно помещаются некоторые особо важные или не подлежащие изменению программы и разнообразные константы. Такой вид памяти часто называют ROM (read only memory), или память только для чтения. Поскольку большая часть этих данных, программ связана с обслуживанием ввода-вывода, то часто содержимое ПЗУ называют BIOS (Basic Input-Output System), базовая система ввода-вывода. В компьютере имеется также небольшой участок полупостоянной памяти для хранения параметров конфигурации компьютера. Ее называют CMOS-памятью. Содержимое этой памяти не изменяется при выключении компьютера, так как ее питание осуществляется от небольшого специального аккумулятора. Для изменения значения параметров конфигурации компьютера в BIOS имеется специальная программа SETUP.
Интерфейсы для устройств ввода и вывода. Они представляют собой блоки сопряжения с устройствами соответственно ввода и вывода. Не останавливаясь пока на описании устройств ввода и вывода, отметим лишь, что термин «интерфейс» означает приблизительно «сопряжение двух устройств друг с другом с помощью аппаратных и программных средств». Необходимость интерфейсов, или, как их еще называют, интерфейсных блоков (контроллеров), вызывается тем, что устройства ввода и вывода (например, дисплей, печатающее устройство, НГМД и т.д.) нельзя непосредственно подключать к компьютеру. Одной из причин этого является то, что количество и характер сигналов, передаваемых и принимаемых по системной магистрали, с которой связаны все компоненты компьютера, как правило, отличаются от количества и типа сигналов, формируемых или воспринимаемых устройством ввода-вывода. Соответствующий интерфейсный блок обеспечивает должное согласование сигналов системной магистрали и устройства ввода-вывода.
На любом персональном компьютере имеются контроллеры для управления клавиатурой, монитором, дисководами для дискет, жестким диском и т.д. Некоторые из контроллеров размещаются на основной системной или материнской плате компьютера, тогда они называются встроенными или интегрированными; а другие на отдельных электронных платах – платах контроллеров. Эти платы соединяются (вставляются) с материнской с помощью специальных разъемов – слотов.
Внешние устройства. Они предназначены для ввода обрабатываемых данных, вывода результатов обработки или вычислений и долговременного запоминания программ и данных.
Основным средством ввода данных на персональном компьютере всегда служит клавиатура. Из других средств ввода-вывода отметим следующие:
1. Накопители (или дисководы) для гибких магнитных дисков, используемые для чтения и записи на гибкие магнитные дискеты. В настоящее время используются дискеты емкостью 1,4 Mb и 2 Mb.
2. Накопитель на жестком магнитном диске, предназначенный для записи и чтения на несъемный жесткий магнитный диск (винчестер). Сейчас применяются в основном винчестеры емкостью в 5-10 GB.
3. Устройства для чтения с компакт дисков, так называемые CD ROMы. Емкость таких дисков обычно составляет 640 Mb. Различаются они скоростью считывания информации, которая может быть сравнена со скоростью работы винчестеров. Они позволяют также проигрывать музыкальные компакт диски.
4. К другим внешним устройствам можно отнести модемы и факс-модемы – для обмена информацией с другими компьютерами через телефонную сеть; стримеры – для хранения данных на магнитной ленте; звуковая карта – для воспроизведения и записи звуков (музыки, голоса и т.д.).
Перечисленные устройства чаще всего размещаются в едином корпусе. Туда же вставляется материнская плата, контроллеры, блок питания . Корпус этот – системный блок по существу и есть компьютер. Из других внешних устройств следует отметить монитор – для вывода информации в графическом и текстовом виде и принтер – для распечатывания документов, манипулятор мышь – для работы в графическом режиме практически незаменима.
Системная магистраль. Обычно она содержит магистрали адресов, данных и управления. Каждый из них состоит из набора проводников, по которым микропроцессор передает или принимает определенные электрические сигналы. Магистраль адреса предназначена для передачи цифрового адреса ячейки памяти или внешнего устройства, магистраль данных – для передачи и приема данных (например, передача информации из микропроцессора в ОЗУ происходит по магистрали данных). Магистраль управления используется для передачи сигналов управления, которые сопровождают любую передачу адреса или данных.
В современных компьютерах чаще всего используются две магистрали (шины) передачи данных между оперативной памятью и контроллерами:
1. Шина ISA для контроллеров с низкой скоростью обмена данными – клавиатура, мышь, дисководы для дискет и т.д.
2. Шина PCI для контроллеров быстрых устройств – жесткие диски, видеоконтроллеры, устройства чтения с компакт дисков и т.д.
Некоторые устройства используют другие шины, например сканер может использовать шину типа SCSI.
Источник питания. Обычно источник питания формирует выпрямленные стабилизированные напряжения +12, -5 и +15 в. Этот набор напряжений может изменяться для различных классов микропроцессоров.
Контрольные вопросы
1. Изобразите структурную схему персонального компьютера.
2. Каким является типовое устройство микропроцессора (модель)?
3. Какие типы микропроцессоров применяются на персональном компьютере?
4. Что такое регистр? Приведите примеры регистров микропроцессора.
5. Устройство управления микропроцессора, что это такое?
6. Какие типы памяти Вы знаете?
7. Что представляет собой кэш-память?
8. Что представляет собой CMOS память?
9. Что такое контроллер, какие типы контроллеров бывают?
10. Какие внешние устройства компьютера Вы знаете?
11. Что такое системная магистраль и какие основные магистрали данных используются в персональном компьютере?
12. Системный блок компьютера, что он включает?
13. Дайте сравнительную характеристику внешних устройств персонального компьютера.
Программное обеспечение ЭВМ
Современные информационно-вычислительные системы, применяемые для решения научно-технических, учетно-плановых и управленческих задач включают две взаимосвязанные, но качественно различные компоненты: комплекс средств вычислительной техники и программное (математическое) обеспечение.
Программное обеспечение (ПО) можно разделить на две части: системное программное обеспечение (СПО) и прикладное программное обеспечение (ППО).
Системное программное обеспечение (СПО) – это комплекс управляющих и обрабатывающих программ, описаний и инструкций, которые обеспечивают техническое функционирование вычислительной системы, а также разработку, отладку и выполнение программ пользователей. Набор программ системного программного обеспечения мало зависит от характера решаемых задач пользователей.
Прикладное программное обеспечение (ППО) представляет собой совокупность программ решения конкретных задач, которые систематически используются в интересах данного предприятия, учреждения или органа управления для обеспечения его производственной, научной или административной деятельности.
Специализированные комплексы программ решения конкретных задач называют пакетами прикладных программ. При создании прикладных программ применяют методы специальных научных, инженерных и экономических дисциплин, а также общие методы вычислительной математики, теории оптимизации, теории информационного поиска и программирования для вычислительных машин.
Разработкой системного программного обеспечения занимается особая дисциплина – системное программирование. Предмет системного программирования – теория и методы разработки и эксплуатации программ системного ПО.
По функциональному назначению и применяемым методам внутри системного программного обеспечения можно выделить две системы программ: операционную систему и систему программирования.
Операционная система есть комплекс управляющих программ, которые обеспечивают техническое функционирование вычислительной системы, включая диагностику неисправностей, планирование использования ресурсов системы и решение задач по управлению заданиями пользователя. Кроме того, на операционную систему часто возлагают управление вводом-выводом и обменом данными между различными компонентами системы (например, между оперативной и внешней памятью), а также ведение архива, т.е. размещение данных во внешней памяти и обеспечение доступа к ним.
Операционную систему можно рассматривать как программное продолжение и расширение аппаратурной части вычислительной системы.
Основной задачей операционной системы является управление выполнением программ пользователей с целью максимального повышения производительности машины.
От выбора операционной системы зависит производительность работы пользователя, степень защиты его данных, необходимое аппаратное и программное обеспечение.
На персональных компьютерах типа IBM PC чаще всего применяются следующие операционные системы:
1. Операционная система MS DOS фирмы Microsoft или совместимые с ней операционные системы – PC DOS фирмы IBM или Novell DOS фирмы Novell;
2. Операционная система Windows 98, Windows NT Workstations или самая новая операционная система Windows 2000 фирмы Microsoft;
3. Операционная система OS/2 Warp одной из версий фирмы IBM;
4. Операционная система Unix или одна из ее модификаций Linux, FreeBSD и т.д.
Помимо операционной системы к системному программному обеспечению относят также драйверы, программы-оболочки, вспомогательные программы или утилиты.
Драйверы являются важнейшим классом системных программ, поскольку они расширяют возможности операционной системы, позволяя ей работать с новыми внешними устройствами. Обычно операционная система содержит некоторый набор драйверов, но чаще всего драйверы поставляются разработчиками новых устройств и контроллеров.
Программы-оболочки обычно представляют собой более удобные средства для общения с ЭВМ, чем стандартные средства ОС. Так для MS DOS это – Norton Commander, для Windows – Norton Navigator и т.д. Причем, чаще всего программы-оболочки не стараются заменить операционную систему, а наоборот пополняют ее новыми, более удобными функциями.
Утилиты или программы обслуживания объединяют большое количество системных программ вспомогательного назначения:
1. Антивирусные программы – основные функции которых - предотвращение заражения компьютера вирусами и ликвидация последствий таких заражений. Различают антивирусные программы детекторы, вакцины, полифаги - в зависимости от их способов борьбы с компьютерными вирусами. В нашей стране наибольшее распространение получили программы AidsTest и Dr.Web.
2. Программы архиваторы или упаковщики позволяют создавать резервные копии файлов, путем уменьшения их размеров за счет выполнения сжатия, уплотнения информации. Наиболее распространены Arj, Zip, Rar для операционных систем MS DOS и Windows.
3. Программы для диагностики технического состояния компьютера, которые позволяют проверять исправность всех устройств компьютера;
4. Программы для оптимизации дисков позволяют обеспечить более быстрый доступ к информации на диске за счет оптимизации размещения данных на диске;
5. Программы ограничения доступа позволяют защитить хранящиеся на компьютере данные от несанкционированного доступа.
Система программирования есть комплекс средств, обеспечивающих автоматизацию программирования и отладки программ. К системе программирования относят библиотеку стандартных подпрограмм, языки программирования и трансляторы, а также отладочные программы. Эти средства предназначены для обеспечения и повышения труда программистов.
Программные компоненты системы программирования выполняются под управлением операционной системы наравне с прикладными программами пользователей. Эти системы обычно включают компилятор, осуществляющий преобразование программ на языке программирования в программу в машинных кодах, или интерпретатор, осуществляющий непосредственное выполнение программы на языке программирования высокого уровня, редактор текстов программ, библиотеки подпрограмм, отладчики и вспомогательные программы.
Для персонального компьютера имеются системы программирования для всех популярных языков программирования, таких как Си, С++, Паскаль, Фортран, Бейсик и т.д. В настоящее время стали распространяться системы программирования с языка Java, позволяющие создавать программы-сценарии для Web-страниц в Интернет.
Особым классом систем программирования являются системы разработки приложений типа клиент-сервер. Они позволяют быстро создавать информационные системы для подразделений и предприятий, с использованием средств визуального программирования. Как правило, эти системы позволяют работать с самыми разными базами данных. Наиболее популярными являются системы Delphi, Visual Basic, C-Builder, Sybase, PowerBuilder, SQLWindows.
Прикладное программное обеспечение насчитывает в своем составе сотни тысяч программ для различных применений. Из всего многообразия прикладных программ можно вычленить следующие группы программ, получивших наибольшее распространение:
1. Редакторы документов, позволяющие подготавливать различные документы высокого качества. Они полностью заменили пишущую машинку, да еще позволили дополнительно выполнять целый ряд функций по подготовке высококачественных документов: управление шрифтами, абзацами, перенос слов, проверка орфографии, вставка рисунков, диаграмм и т.д. Наиболее популярны для ОС MS DOS ЛЕКСИКОН, Microsoft Word, WordPerfect, а для Windows – Microsoft Word, Corel WordPerfect, Word Pro фирмы Lotus, Just Write фирмы Symantec.
2. Табличные процессоры, представляющие документ в виде таблицы из прямоугольных клеток, в которых могут храниться числа, формулы, пояснительные тексты. Все распространенные табличные процессоры позволяют производить перевычисление значений, строить различные графики, включать в таблицы рисунки, использовать макрокоманды, работать с базами данных. Наибольшей популярностью пользуются Microsoft Excel, Lotus 1-2-3, Quattro Pro.
3. Издательские системы предназначены для подготовки рекламных буклетов, оформления газет, журналов, книг. Их основная функция – верстка, т.е. размещение текста, рисунков и пр. на страницах документа. Наибольшую популярность получили издательские системы – PageMaker фирмы Adobe и QuarkXpress фирмы Quark.
4. Программы подготовки презентаций могут оформлять слайды для презентаций, помещая туда красивые диаграммы, рисунки, надписи, включать звуковое сопровождение и показывать презентации на компьютере. Наиболее известны программ – PowerPoint фирмы Microsoft, Harvard Graphics фирмы Software Publishing.
5. Графические редакторы, позволяющие работать с графическими объектами – рисунками, фотографиями. Наиболее известны - Adobe PhotoShop, Corel Draw.
6. Анимационные программы позволяют создавать трехмерные движущиеся модели объектов, создавать анимационные фильмы. Примером может служить программа 3D Studio фирмы Autodesk.
7. Программы для создания компьютерного видео при наличии соответствующего оборудования производить монтаж видеофильмов, накладывать титры, видеоэффекты. Пример такой программы – Adobe Premiere.
8. Бухгалтерские программы позволяют вести бухгалтерский учет, подготавливать финансовую отчетность. Наибольшее распространение получили – 1С-бухгалтерия, Инфо-Бухгалтер. Для предприятий с большим объемом хозяйственных операций, многие из которых уже не относятся к бухгалтерскому учету – складской учет, учет торговых операций, контроль за выполнением договоров, управленческий учет, финансовый анализ деятельности предприятия, целесообразно применение программных комплексов: Парус, Инфософт, Инфин и т.д.
9. Правовые базы данных содержат тексты нормативных документов и предоставляют возможности поиска и распечатки, например, Гарант, Кодекс, Юрисконсульт.
10. Персональные информационные менеджеры позволяю назначать разовые и повторяющиеся мероприятия, напоминать о делах, встречах, облегчают звонки по телефону. Пример таких программ: Lotus Organizer, Sidekick фирмы Starfish Software.
11. Программы планирования позволяют составлять план-графики работ, например, Microsoft Project, TimeLine фирмы Semantic.
12. Программы распознавания символов позволят вводить с помощью сканера напечатанные тексты, рисунки, графики, фотографии. У нас получила наибольшее распространение программа FineReader фирмы Бит.
13. Программы переводчики позволяют переводить с одного языка на другой с более менее пристойным качеством, например, Stylus фирмы ПроМТ, Сократ фирмы АрсеналЪ.
14. Программы словари (Мультилекс фирмы МедиаЛингва, Контекст фирмы Информатик, Лингво фирмы Бит) – это электронные версии обычных словарей с некоторыми дополнительными возможностями.
15. Системы управления базами данных позволяют управлять большими информационными массивами. Так, весьма мощны и удобны в использовании Lotus Approach, DataEase, Paradox, FoxPro, Access. Для создания больших и многопользовательских информационных систем типа клиент-сервер широко используются Oracle, Microsoft SQL Server, Sybase SQL Server, Iformix.
16. Системы автоматического проектирования (САПР) позволяют осуществлять черчение и конструирование различных предметов и механизмов с помощью компьютера. Среди систем малого и среднего класса наиболее популярна система AutoCad фирмы AutoDesk. Системы более высокого класса включают средства трехмерного моделирования, процессов механобработки, программирования оборудования с числовым программным управлением. Здесь можно отметить системы «Компас» фирмы Аскон и T-Flex CAD фирмы Топсистемы.
17. Программы для Интернет. Сюда включается великое множество программ по поиску информации, осуществления связи в реальном времени, созданию Web-страниц, всевозможные броузеры и средства для электронной почты. Интернет непрерывно развивается, с ним получает мощнейшее развитие и вся программная индустрия для Интернет.
Большинство программ для персонального компьютера распространяется на коммерческой основе, но имеются и другие формы распространения программ. Так получила большое распространение бесплатная форма распространения программ (freeware) сети Интернет и электронных досок объявлений (BBS). Промежуточное положение между бесплатными и коммерческими программами занимают условно бесплатные программы (shareware). Их можно получить и опробовать некоторое время бесплатно, но при систематическом их использовании необходимо уплатить разработчику определенную (чаще всего небольшую) сумму. В наше использование чаще всего попадают пиратские копии программ (незаконные, взломанные копии коммерческих и условно бесплатных программ), не имеющие ни документации, ни гарантии правильной работы.
Контрольные вопросы
1. На какие части делится программное обеспечение для персонального компьютера?
2. Что такое системное программное обеспечение? Какое программное обеспечение оно включает?
3. Что такое система программирования?
4. Какие классы наиболее распространенного прикладного программного обеспечения вы знаете?
5. Каковы основные функции операционной системы?
6. Приведите примеры наиболее распространенных операционных систем для персонального компьютера?
7. В чем отличие компилятора от интерпретатора?
8. Что такое технология клиент-сервер?
9. Приведите примеры наиболее распространенных антивирусных программ.
10. Дайте классификацию антивирусных программ.
11. Каково назначение программ-архиваторов?
12. Какие основные способы распространения программного обеспечения Вы знаете?
Алгоритмы. Определение и свойства алгоритмов
Широкая известность понятия алгоритма в наше время обусловлена развитием и широким применением электронно-вычислительной техники. Использование ЭВМ способствовала уяснению того, что разработка алгоритма – необходимый этап в процессе решения задачи на ЭВМ и что в связи с этим алгоритмы представляют самостоятельную ценность как интеллектуальные ресурсы общества.
Понятие алгоритма, относящиеся к фундаментальным концепциям информатики, возникло задолго до появления ЭВМ и стало одним из основных понятий математики.
Слово «алгоритм» произошло от имени среднеазиатского (узбекского) математика аль-Хорезми (IХ в.) и использовалось в математике для обозначения правил выполнения четырех арифметических действий: сложения, вычитания, умножения, деления. В настоящее время понятие алгоритма используется не только в математике. Его применяют во многих областях человеческой деятельности, например говорят об алгоритме управления производственным процессом, алгоритме игры в шахматы, алгоритме пользования бытовым прибором, алгоритме поиска пути в лабиринте, алгоритме управления полётом ракеты и т.п.
Для пояснения понятия «алгоритм» важное значение имеет определение понятия «исполнитель алгоритма». Алгоритм формулируется в расчете на конкретного исполнителя, например человека, специально дрессированное животное, особую машину – автомат и т.д. Алгоритм является руководством к действию для исполнителя, поэтому значение слова «алгоритм» близко по смыслу к значению слов «указание» или «предписание». Можно сказать, что алгоритм – понятное и точное предписание (указание) исполнителю совершить определённую последовательность действий для достижения указанной цели или решения поставленной задачи. Сказанное не является определением в математическом смысле, а лишь отражает интуитивное понимание алгоритма, сложившееся за долгие годы.
Пример 1. Пусть имеется текст на русском языке, подготовленный специальным образом, который заканчивается специальным символом @, больше нигде в тексте не встречающемся. Необходимо подсчитать число гласных букв в данном тексте.
Для решения этой задачи можно предложить такой способ подсчета числа гласных букв: читать последовательно символ за символом и каждый раз, когда очередной символ есть гласная буква русского алфавита, прибавлять к счетчику единицу (предполагается, что исполнитель данного алгоритма умеет различать гласные и не гласные буквы). Счет начинать с нуля и продолжать до тех пор, пока не будет прочитан символ @, обозначающий конец текста. Приведенное выше описание дает лишь идею алгоритма, но, чтобы превратить его в понятное и точное предписание исполнителю, его необходимо уточнить.
Во–первых, объектами алгоритма являются символы текста и числа. Над символами текста производятся операции чтения, поиска следующего символа, сравнения символа с символом @ и сравнение символа с одной из гласных букв русского алфавита. Над числами производится операция прибавления единицы.
Во–вторых, символы текста читаются последовательно один за другим, начиная с первого символа до символа @ включительно. Чтобы не ошибиться при чтении, будем предполагать, что наш абстрактный исполнитель имеет в своем распоряжении указатель, который можно перемещать по тексту и который указывает на очередной читаемый символ. Поэтому поиск следующего символа сводится к перемещению указателя на следующий по порядку символ текста.
В–третьих, счет числа гласных букв начинается с нуля, поэтому до начала работы счетчик числа гласных должен содержать нуль.
Учитывая эти замечания, сформулируем алгоритм в виде такой последовательности действий:
1. Записать в счетчик 0.
2. Установить указатель на первый символ текста.
3. Если символ не есть @, то перейти к п.4, иначе перейти к пункту 7.
4. Если символ – гласная буква русского алфавита, то увеличить счетчик на единицу.
5. Перевести указатель на следующий символ текста.
6. Перейти к п.3.
7. Взять число, находящееся в счетчике, в качестве ответа. Стоп.
Обратим внимание на основные особенности (свойства) алгоритма.
1. Алгоритм имеет некоторое число входных величин – аргументов, задаваемых до начала работы (в приведенном выше примере входными данными являются символы текста и возможно набор гласных букв).
Цель выполнения алгоритма – получение результата (результатов), имеющего вполне определенное отношение к исходным данным.
В данном примере результат – число, обозначающее число гласных букв в исходном тексте.
Для алгоритма можно брать различные наборы входных данных, т.е. применять один и тот же алгоритм для решения целого класса однотипных задач, различающихся исходными данными. Это свойство алгоритма обычно называют массовостью. Рассмотренный в примере алгоритм применим к различным текстам на русском языке. Вместе с тем существуют и такие алгоритмы, которые применимы только к единственному набору исходных данных. Например, для алгоритма пользования автоматическим турникетом при входе в метро существует единственный вариант исходного данного – тридцати копеечный жетон. Поэтому понятие массовости требует уточнения. Можно считать, что для каждого алгоритма существует свой класс объектов, допустимых в качестве исходных данных. Тогда свойство массовости означает применимость алгоритма ко всем объектам этого класса. А количество объектов класса (конечное или бесконечное) – свойство самого класса исходных данных.
2. Чтобы алгоритм можно было выполнить, он должен быть понятен исполнителю. Приведенный в примере алгоритм подсчета гласных букв может быть понятен человеку, знающему русский язык. Чтобы этот алгоритм мог быть также выполнен человеком, не знающим русского языка, необходимо записать алгоритм на языке понятном исполнителю, и сообщить ему дополнительные сведения: перечислить явно гласные буквы русского алфавита.
Понятность алгоритма означает знание исполнителя о том, что надо делать для исполнения этого алгоритма.
Таким образом, при формулировке алгоритма необходимо учитывать возможности и особенности исполнителя, на которого рассчитан алгоритм.
3. Алгоритм представлен в виде конечной последовательности шагов. Говорят, что алгоритм имеет дискретную структуру. Следовательно, его исполнение расчленяется на выполнение отдельных его шагов, выполнение каждого очередного шага начинается после завершения предыдущего.
4. Выполнение алгоритма заканчивается после выполнения конечного числа шагов. При выполнении алгоритма некоторые его шаги могут повторяться многократно. В рассмотренном выше примере многократно повторяются шаги с третьего по шестой. Однако выполнение алгоритма все же закончится за конечное число шагов, так как текст имеет конечную длину и в нем имеется символ @. При чтении этого символа будет выполнен седьмой шаг алгоритма, завершающий его выполнение.
В математике существуют вычислительные процедуры, имеющие алгоритмический характер, но не обладающие свойством конечности. Так, можно сформулировать процедуру вычисления числа Пи. Такая процедура описывает бесконечный процесс и никогда не завершится. Если же ее искусственно прервать, например ввести условие завершения процесса вычислений вида: «Закончить вычисления после получения N десятичных знаков числа Пи», то получится алгоритм вычисления N десятичных знаков числа Пи. На этом принципе основано получение многих вычислительных алгоритмов: строится бесконечный, сходящийся к искомому решению процесс. Он обрывается на некотором шаге, и полученное значение принимается за приближенное решение рассматриваемой задачи. При этом точность приближения зависит от числа шагов.
5. Каждый шаг алгоритма должен быть четко и недвусмысленно определен и не должен допускать произвольной трактовки исполнителем. При исполнении алгоритма исполнитель должен действовать строго в соответствии с его правилами и у него не должно возникать потребности предпринимать какие-нибудь действия, отличные от предписанных алгоритмом. Иными словами, алгоритм рассчитан на чисто механическое исполнение. Эта очень важная особенность означает, в частности, что если один и тот же алгоритм поручить для исполнения разным исполнителям, то они придут к одному и тому же результату, лишь бы эти исполнители понимали алгоритм. Именно определенность алгоритма дает возможность поручить его исполнение автомату, не обладающему «здравым смыслом».
B приведенном выше примере, действие перемещения указателя на следующий символ достаточно точно определено, если текст расположен на длинной узкой ленте и вытянут в одну строку (например, напечатан на узкой телетайпной ленте). Если же текст разбит на строки и страницы (т.е. имеет сложную структуру), то действие перемещения указателя на следующий символ уже не является столь очевидным. В этом случае необходимы указания, как поступать исполнителю, когда закончится очередная строка или очередная страница текста.
Таким образом, формулировка алгоритма должна быть так точна, чтобы полностью определять все действия исполнителя.
6. Каждый шаг алгоритма должен быть выполнен точно и за конечное время. В этом смысле говорят, что алгоритм должен быть эффективным, т.е. действия исполнителя на каждом шаге исполнения алгоритма должны быть достаточно простыми, чтобы их можно было выполнить точно и за конечное время. Поэтому, например, указание вида: «Если любое целое число, большее 6, можно представить в виде суммы трех простых чисел, то счетчик увеличить на 1, иначе счетчик уменьшить на 1» – неэффективно, так как не известен способ доказательства истинности или ложности утверждения, содержащегося в нем. Следовательно, исполнитель не может выполнить этот шаг алгоритма, пока не найдет соответствующего доказательства.
Обычно отдельные указания исполнителю, содержащиеся в каждом шаге алгоритма, называют командами. Таким образом, эффективность алгоритма связана с возможностью выполнения каждой команды за конечное время. Исполнители отличаются друг от друга своими возможностями, т.е. репертуаром команд, которые они «понимают» и могут выполнять. Совокупность команд, которые могут быть выполнены конкретным исполнителем, называется системой команд исполнителя. Следовательно, алгоритм, рассчитанный на конкретного исполнителя, должен быть сформулирован так, чтобы содержать только те команды, которые входят в систему команд этого исполнителя.
Кроме того, эффективность означает, что алгоритм может быть выполнен не просто за конечное, а за разумное конечное время (обычно важно, чтобы задача по разработанному алгоритму решалась как можно быстрее). Вот почему при разработке алгоритмов должны учитываться и возможности конкретных физических исполнителей алгоритма.
Приведенные выше комментарии поясняют интуитивное понятие алгоритма, но само это понятие не становиться от этого более четким и строгим. Тем не менее математики долгое время довольствовались этим понятием. Лишь с выявлением алгоритмически неразрешимых задач. т.е. задач, для решения которых невозможно построить алгоритм, появилось настоятельная потребность в построении формального определения алгоритма, соответствующего известному интуитивному понятию.
Интуитивное понятие алгоритма в силу своей расплывчатости не может быть объектом математического изучения, поэтому для доказательства существования или не существование алгоритма решения задачи было необходимо строгое формальное определение алгоритма.
Построение такого формального определение было начато с формализации объектов (операндов) алгоритма, так как в интуитивном понятии алгоритма его объекты могут иметь произвольную природу. Ими могут быть, например, числа, показания датчиков, фиксирующих параметры производственного процесса, шахматные фигуры и позиции и т.п. Однако, предполагая, что алгоритм имеет дело не с самими реальными объектами, а с их изображениями, можно считать, что операнды алгоритма есть слова в произвольном алфавите. Тогда получается, что алгоритм преобразует слова в произвольном алфавите в слова того же алфавита. Дальнейшая формализация понятия алгоритм связана с формализацией действий над операндами и порядка этих действий. Одна из таких формализаций была предложена английским математиком А.Тьюрингом в 1936 году, который формально описал конструкцию некоторой абстрактной машины (машины Тьюринга) как исполнителя алгоритма и высказал тезис о том, что всякий алгоритм может быть реализован соответствующей машиной Тьюринга.
Мы будем придерживаться неформального определения алгоритма, формулируемого следующим образом:
Алгоритм - это упорядоченная последовательность указаний, выполнение которой приводит от исходных данных к требуемому результату.
Другими словами алгоритм это план решения задачи, записанный в виде последовательности указаний или групп указаний.
Приведем пример алгоритма Евклида, выполняя который определяется общий наибольший делитель двух положительных целых чисел a и b.
Пример 2. Алгоритм Евклида, нахождения наибольшего общего делителя двух положительных чисел.
1. Проверить a> b. Если да, то перейти к указанию 2, иначе – к указанию 3.
2. Взять за новое значение a разность a- b. Перейти к указанию 1.
3. Проверить b> a . Если да, то перейти к указанию 4, иначе - к указанию 5.
4. Взять за новое значение b разность b- a, перейти к указание 1.
5. За результат взять последнее значение a ( b). Перейти к указанию 6.
6. Закончить процесс.
В приведенном выше алгоритме, предполагается, что его может выполнить любой человек или вычислительная машина, который умеет выполнять операции сравнения и вычитания двух чисел. Напомним, что в школе наибольший общий делитель определяется как произведение общих простых делителей чисел. В данном алгоритме о произведении и понятии делителя числа нет даже упоминания и, тем не менее, следуя ему, всегда определяется наибольший общий делитель двух целых положительных чисел. Это факт говорит о том, что получить результат можно разными способами с применением операций, которые, на первый взгляд, не имеют к решаемой проблеме никакого отношения, что позволяет среди всех возможных вариантов решения задачи, искать наиболее эффективный. В дальнейшем рассматриваются алгоритмы для вычислительных машин. Современные компьютеры с мощным программным обеспечением могут выполнять различные операции: от простых арифметических операций, производимых над двумя числами до решения сложных задач из многих сфер деятельности людей. Если на компьютере имеется программа, позволяющая решить требуемую задачу, то алгоритм решения такой задачи сводится к описанию процесса ввода исходных данных, обращения к требуемой программе и получения результатов в нужном виде. В тоже время для очень многих простых задач нет готовых программ их решения. По-видимому, нельзя на все случаи, да и нет такой необходимости, хранить в памяти необходимые программы. Но практически все программные системы, применяемые на компьютерах, имеют реализованные языки программирования, позволяющие с небольшими затратами составить самостоятельно программу решения довольно сложной задачи. Для реализации такой возможности надо уметь составлять алгоритмы и знать правила (синтаксис) записи указаний на алгоритмическом языке. В дальнейшем мы предполагаем, что «машина умеет» выполнять все арифметические операции, операции сравнения, логические операции, а также может вычислять практически все элементарные функции. Кроме этого она может ввести в память необходимые данные, а также напечатать или вывести на дисплей результаты.
Таким образом, алгоритмы должны обладать такими основными свойствами: массовостью (результативностью); понятностью; дискретностью; конечностью; определенностью; эффективностью.
Среди других свойств алгоритмов, следует отметить оптимальность и элегантность. Правда понятие оптимальности в алгоритмах имеет компромиссный характер, так как можно оптимизировать количество необходимых для получения результата операций, или объем требуемой памяти, или скорость выполнения и даже понятность алгоритма. Поэтому, составляя алгоритм, следует определиться, что надо оптимизировать в первую очередь и как этого достичь. Составление алгоритмов является не только трудоемким процессом, но и, в некотором смысле искусством, поэтому так ценятся хорошие элегантные алгоритмы. Составление алгоритма предполагает от составителя следующего:
· Ясное понимание хода решения задачи, а лучше нескольких вариантов, получения решения, начиная с ввода (определения) исходных данных.
· Знание возможностей исполнителя по выполнению тех указаний, с помощью которых записывается данный алгоритм.
· Если алгоритм составляется под написание программы на алгоритмическом языке, то желательно для составителя алгоритма иметь хорошее представление о синтаксисе языка и наборе операторов языка.
Дата: 2019-07-30, просмотров: 347.