Рассмотрим функцию, которая связывает характеристики разомкнутых и замкнутых дискретных систем
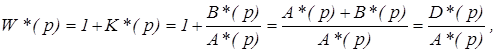 (12)
(12)
где D*(p) – характеристический полином замкнутой системы;
A*(p) – характеристический полином разомкнутой системы.
В соответствии со следствием из принципа аргумента
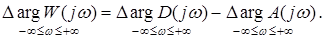 (13)
(13)
Рассмотрим разные случаи.
Система, устойчивая в разомкнутом состоянии
Так как разомкнутая дискретная система устойчива, то она не содержит корней в правой полуплоскости (т. е. m = 0), для того чтобы и замкнутая дискретная система была устойчива, должно выполняться условие
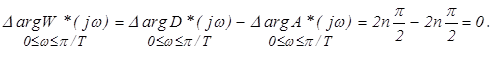 (14)
(14)
Формулировка критерия Найквиста:
Замкнутая дискретная система устойчива, если амплитудно-фазовая частотная характеристика разомкнутой устойчивой системы не охватывает току с координатами (–1,j0).
Графически это обозначает, что годограф вектора W*(j w ) не охватывает начала координат, а вектора K*(j w ) -точку с координатами (-1, j0).
Система, неустойчивая в разомкнутом состоянии
Так как разомкнутая система неустойчива, то она содержит m корней в правой полуплоскости, для того чтобы замкнутая система была устойчива, должно выполняться условие:
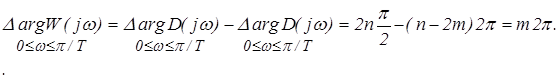
Графически это обозначает, что годограф вектора K(j w ) охватывает точку с координатами (-1, j0) m –раз.
Формулировка критерия Найквиста: Замкнутая дискретная система устойчива, если амплитудно-фазовая частотная характеристика разомкнутой неустойчивой системы, имеющей m корней в правой полуплоскости, охватывает току с координатами (–1 , j0) m раз.
Пример 10. Определить условия устойчивости и величину критического коэффициента усиления по критерию Найквиста дискретной системы, схема которой приведена на рис. 6.
Решение: Передаточная функция разомкнутой дискретной системы в форме z– преобразования
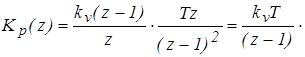
При этом выражение для частотной характеристики имеет вид

Строим частотную характеристику дискретной системы в соответствии с таблицами 2 и 3 (рис. 9).
Характеристику строим на интервале частот 0 £ w £ p /T в дальнейшем характеристики повторяются, так как они носят периодический характер.
Условие устойчивости данной дискретной системы определяется соотношением kvT/2 = 1. 0 £ w £ p/T
Таблица 2
| w | 0 | p/2T | p/T |
| P*(w) | -kvT/2 | -kvT/2 | -kvT/2 |
| Q*(w) | -¥ | -kvT/2 | 0 |
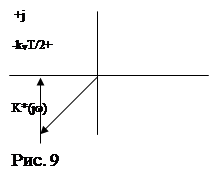 |
Таблица 3
| a | 0 | 30 | 45 | 60 | 90 |
| ctga | -¥ | Ö3 | 1 | 1/Ö3 | 0 |
Критический коэффициент усиления системы равен kv кр = 2/Т.
Литература
1. Дорф Р., Бишоп Р. Автоматика. Современные системы управления. 2002г. – 832с.
2. Харазов В. Г. Интегрированные системы управления технологическими процессами: Справочник. Издательство: ПРОФЕССИЯ, ИЗДАТЕЛЬСТВО, 2009. – 550с.
3. Чебурахин И. Синтез дискретных управляющих систем и математическое моделирование: теория, алгоритмы, программы. Изд-во: НИЦ РХД, ФИЗМАТЛИТ®, 2004. – 248c.
Дата: 2019-07-30, просмотров: 326.