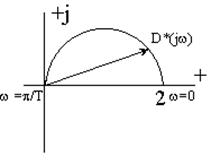
Доказательство частотных критериев устойчивости базируется на следствии из принципа аргумента. Рассмотрим, как он формулируется для дискретных систем.
Пусть задано характеристическое уравнение замкнутой системы
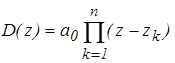 . (8)
. (8)
Рассмотрим комплексную плоскость Z (рис. 7), пусть z2 расположен внутри круга единичного радиуса, а z1 вне него.
При этом
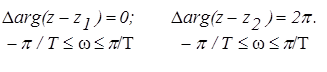 (9)
(9)
Если замкнутая система устойчива, то все корни расположены в пределах окружности единичного радиуса, а значит
 (10)
(10)
Замкнутая дискретная система устойчива, если характеристическая кривая D*(jw) при изменении частоты 0 £ w £ p/T последовательно проходит 2n квадрантов.
Порядок построения характеристической кривой: определяем D(z); выполняем подстановку 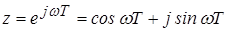 ; определяем выражение
; определяем выражение
 ;
;
изменяя 0 £ w £ p /T строим D*(j w ) (рис. 5).
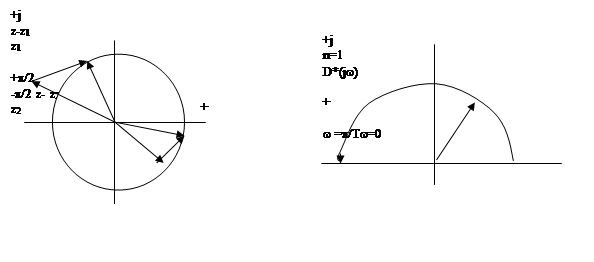 |
а) б)
Рис. 5
Пример 8. Определить устойчивость по критерию Михайлова системы, схема которой приведена на рис. 6, если T = 1 с, kv = 2 c-1.
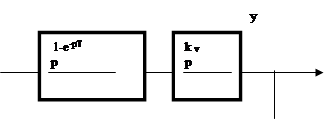 | |||
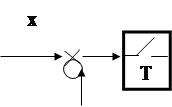 | |||
 -
-
Рис.6
Решение: Передаточная функция разомкнутой системы
 .
.
Передаточная функция разомкнутой дискретной системы
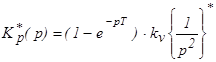 .
.
Передаточная функция разомкнутой дискретной системы в форме z– преобразования
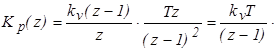
Передаточная функция замкнутой дискретной системы в форме z – преобразования
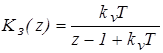 .
.
Характеристический полином имеет вид
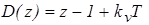 .
.
Определяем выражение
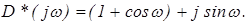
Изменяя частоту в пределах 0 £ w £ p (0 £ w £ p/T) строим годограф Михайлова (рис. 7).
|
Таблица 1
|
| w | 0 | p/4 | p/2 | p3/4 | p |
| X*(w) | 2 | 1+Ö2/2 | 1 | 1-Ö2/2 | 0 |
| Y*(w) | 0 | Ö2/2 | 1 | Ö2/2 | 0 |
Как видно из рисунка система находится на границе устойчивости.
Проверим по критерию Гурвица при
kvT = 2; z+1 = 0; z1 = -1; 1 z11=1.
Корень находится на окружности единичного радиуса, следовательно, система находится на границе устойчивости.
Критерий устойчивости Михайлова с использованием билинейного преобразования
При этом исходным является характеристический полином в форме z-преобразования. Выполним подстановку
z = (1+w)/(1-w) .
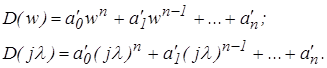 (11)
(11)
Пусть: w = j l, где l–фиктивная частота (0 £ l £ ¥).
При этом критерий Михайлова для дискретных систем применяется в таком же виде, как и для непрерывных систем.
Пример 9. Определить условие устойчивости по критерию Михайлова дискретной системы, схема которой приведена на рис. 6.
Решение:
Характеристический полином имеет вид
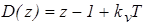 .
.
Выполнив подстановку z = (1+w)/(1-w), в характеристический полином получим
 .
.
Выполнив подстановку w = j l, в характеристический полином получим

Строим график рис. 8. Система устойчива при kvT > 2. Критический коэффициент усиления равен kv кр = 2/T.
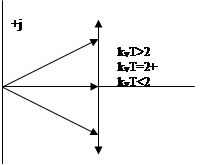
Рис. 8
Дата: 2019-07-30, просмотров: 301.