Как уже говорилось в курсе механики, колебания - это изменение состояния системы. Электромагнитные колебания предполагают изменение тока, заряда или же напряжения. В школьном курсе физики такого типа колебания рассматриваются на примере колебательного контура. Данные изменения происходят в конденсаторе и в катушке. Электромагнитные колебания в контуре происходят только за счет энергии, которая сберегается в конденсаторе и катушке, без посторонней силы. Принято считать, что в катушке сопротивление отсутствует. Время, за которое происходит одно колебание, будем считать равным 1 периоду.

В начальный момент на конденсаторе сохранен заряд размером q₀. После этого ток начнет постепенно перемещаться на катушку, однако, моментально принять максимальное значение он не может, поэтому происходит его изменение, в результате чего изменяется магнитное поле и тем самым появляется самоиндукция. Она, в свою очередь, пытается противодействовать возрастанию тока, поэтому так же увеличивается.

Чтобы стало более понятно, давайте представим пружинный маятник. В начальный момент пружина растянута до максимального значения. В это время скорость его является нулевой, однако в тот момент, когда маятник отпускают, он начинает ускоряться благодаря силам упругости, но, чем ближе к нерастянутому положению, тем меньше данная скорость становится.

Итак, по истечению первой четверти периода катушка максимально наполняется током, а конденсатор, наоборот, отдал весь заряд. На протяжении второй четверти заряд переходит на конденсатор и снова постепенно его заряжает. Следует отметить, что не происходит моментально зарядки или разрядки конденсатора - заряд с него уходит постепенно.

Во время перезарядки конденсатора обкладки наполняются зарядом, противоположным первоначальному. Полностью конденсатор перезаряжается только по прошествии первой половины периода. После этого происходят такие же изменения в контуре, но в обратном направлении.

И когда обкладки конденсатора полностью зарядятся точно так же, как и было в начальный момент времени - пройдет период.

Если в контуре отсутствует сопротивление, то такие колебания будут продолжаться бесконечно долго, без изменения амплитуды. Если же рассматривать подобную цепь в реальной жизни, то за каждый период на конденсатор будет возвращаться меньшее количество заряда, поэтому величина тока будет постепенно падать. В конечном итоге, из-за сопротивления он полностью потухнет.

Гармонические колебания.

Колебания в идеальном контуре можно описать с помощью законов синуса и косинуса. При этом ток - производная заряда.

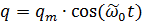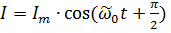 ,  , где

q и q_m – мгновенное и максимальное значения заряда конденсатора,

I и I_m – мгновенное и максимальное значения силы тока,

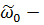циклическая частота колебаний.

    При рассмотрении колебаний в механике мы рассматривали, что на период колебаний математического маятника влияет длина нити и ускорение свободного падения, в пружинном маятнике - масса груза и жесткость пружины. В данном случае основными величинами, которые влияют на период, являются емкость конденсатора и индуктивность. Формула для нахождения периода называется формулой Томсона:

   ,  .

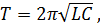
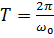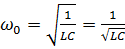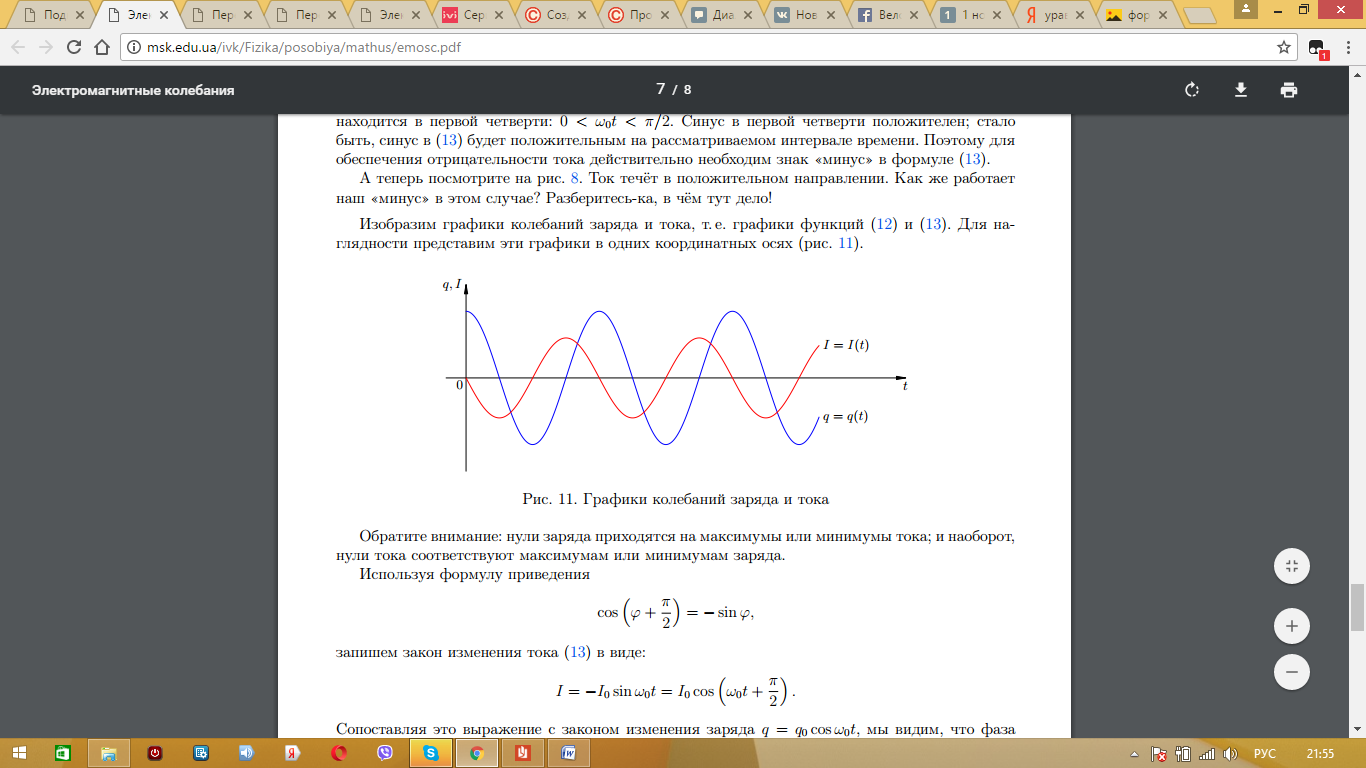
Во время колебаний в колебательном контуре происходит переход заряда из конденсатора в катушку и обратно. В каждой из частей такого контура электромагнитное поле совершает определенную работу. Поэтому для такого перемещения заряда и тока необходима энергия. Так же, как и в случае с описанием каждой части периода, так и с энергией имеется такая же зависимость. В момент, когда максимальный заряд находится на конденсаторе, он имеет максимальное значение энергии, а энергия на катушке равна нулю. После того, как весь ток перешел на катушку - энергия катушки максимальна, а на конденсаторе равна нулю. Но все мы знаем, что в природе существует закон сохранения заряда. Поэтому максимальное значение энергии на конденсаторе равно максимальной энергии на катушке. Максимальная энергия конденсатора:  .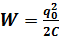

Максимальная энергия катушки:  .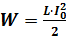

Энергия контура в произвольный момент времени:  .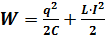

Но все выражения, представленные выше, равны между собой:

  .

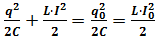До сих пор речь шла о свободных колебаниях, которые происходят в результате собственных сил рассматриваемой цепи. Сейчас же речь пойдет о контуре, на который действует внешняя сила. Такие колебания называются вынужденными. Чтобы получить вынужденные колебания, цепь должна быть подключена к источнику току, в который происходят гармонические колебания напряжения. При этом частота источника тока должна совпадать с частотой контура. Это означает, что, если источник тока вырабатывает напряжение:  .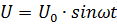

Контур имеет частоту, равную ω. Отсюда следует, что период будет находиться следующим образом: 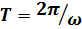, а частота:  .

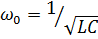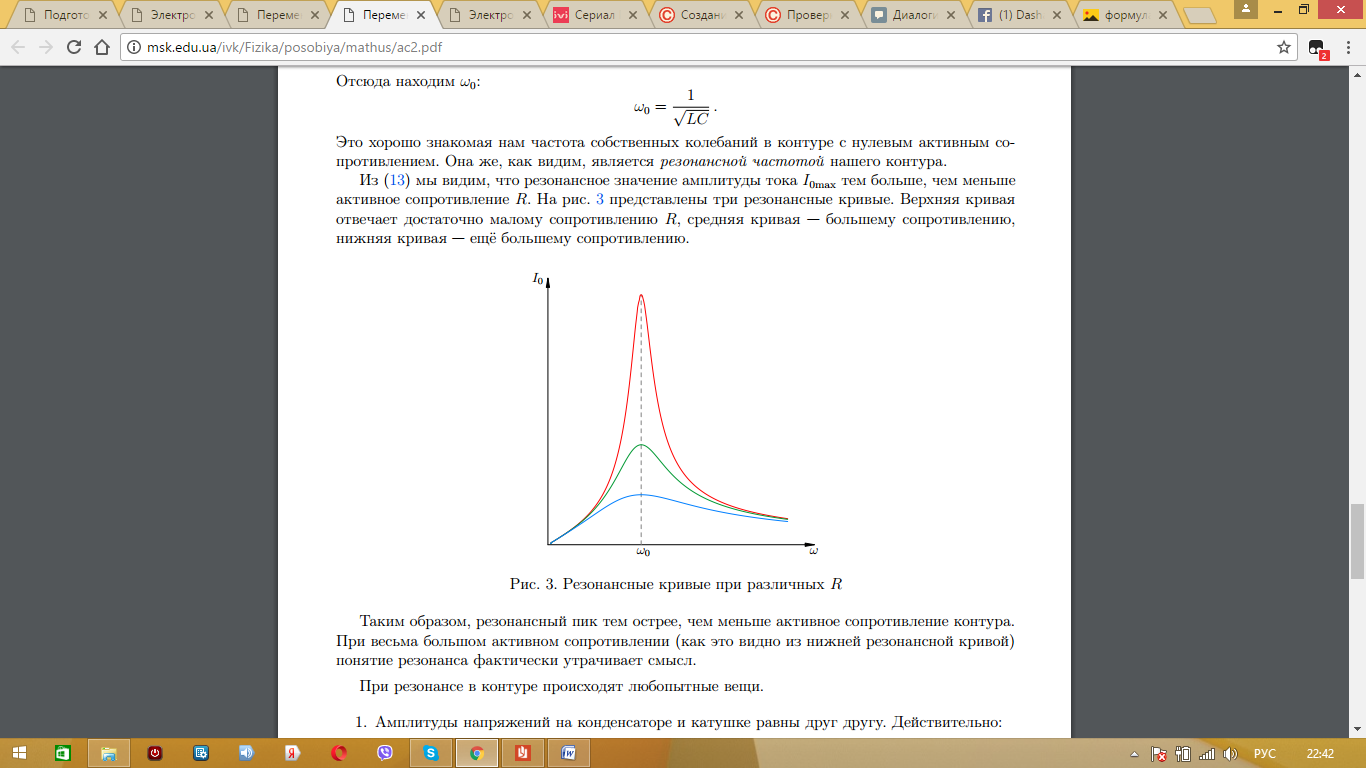
При этом стоит обратить внимание, что значение амплитуды тока в контуре зависит от величины частоты самого контура и от частоты источника тока. Если эти частоты стремятся друг к другу, то в контуре наблюдается резонанс - резкий скачек амплитуды. Это происходит в том случае, когда выполняется следующее равенство: 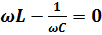 . Во время резонанса амплитуды на конденсаторе и на катушке равны между собой. При такой ситуации не существует сдвига фаз для тока и напряжения. На графике резонанс колебательного контура показывается следующим образом:

Переменный ток - это колебания, которые могут происходить в цепи в результате подключения её к источнику переменного напряжения. Переменный ток - он имеется во всех цепях в квартирах, происходит передача по проводам именно тока переменного напряжения. Однако, практически все электроприборы работают от постоянно электричества, так как на выходе из розетки ток выпрямляется и в виде постоянного переходит к бытовой технике. Именно переменный ток проще всего получить и передать на любое расстояние.

Соберем цепь, в которую будем подключать резистор, катушку и конденсатор. В данной цепи напряжение определяется по закону:

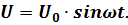 Синус может принимать отрицательные и положительные значения, следовательно, заметим, что напряжение может принимать различное направление. Рассмотрим случай, когда в цепь с переменным током подключен только резистор. Сопротивление резистора называется активным. Будем рассматривать ток, который течет по цепи против часовой стрелки. В таком случае и ток, и напряжение будут иметь положительное значение. Для определения силы тока в цепи используют следующую формулу из закона Ома:  ,  .

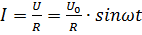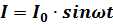В этих формулах I₀ и U₀ - максимальные значения тока и напряжения. Отсюда можно сделать вывод, что максимальное значение тока равно отношению максимального напряжения к активному сопротивлению: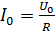  

Эти две величины, сила тока и напряжение цепи, изменяются в одинаковой фазе, поэтому графики величин имеют одинаковый вид, но разные амплитуды.

Конденсатор в цепи.

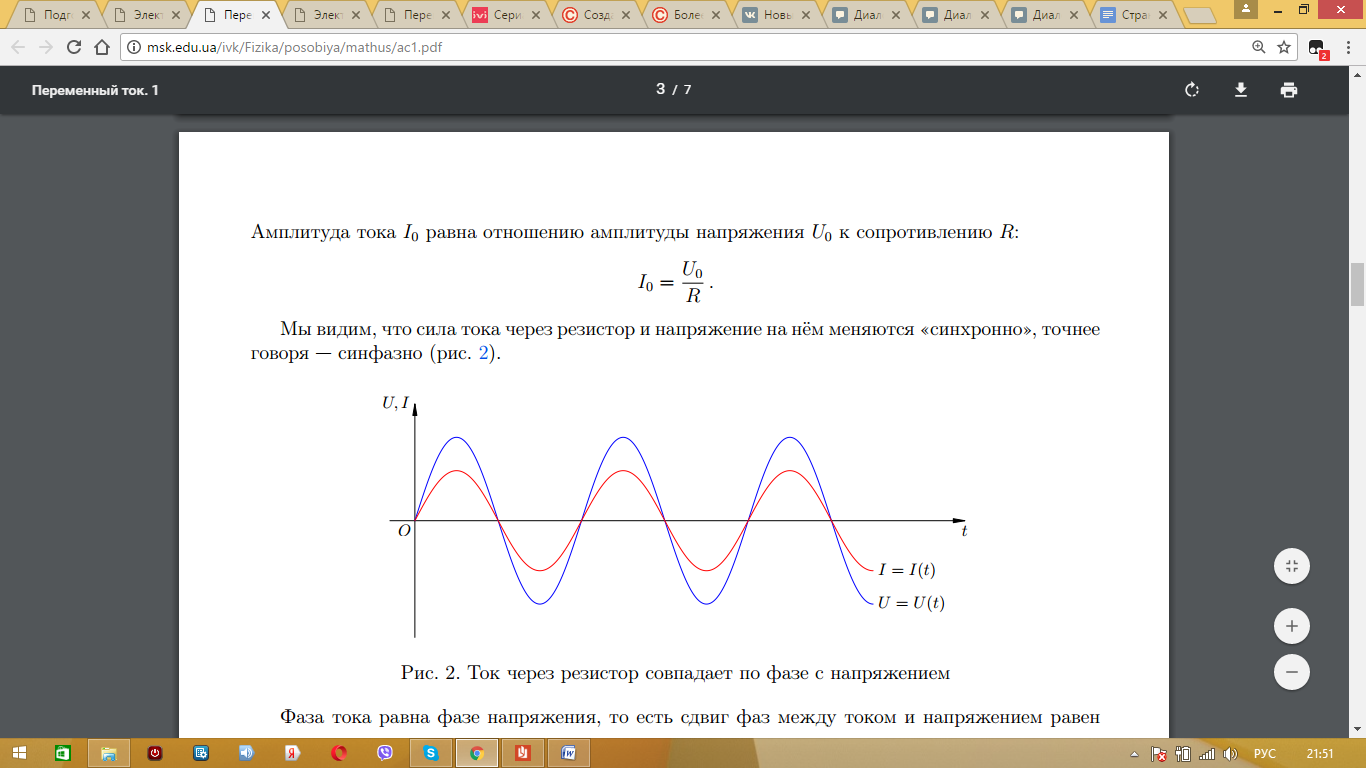
Запомните! Невозможно получить постоянный ток в той цепи, где есть конденсатор. Он является местом для разрыва протекания тока и изменение его амплитуды. При этом переменный ток отлично течет по такой цепи, изменяя полярность конденсатора. Рассмотрим цепь, в которой имеется исключительно конденсатор. Ток течет против часовой стрелки, то есть является положительным. Напряжение на конденсаторе связано с его возможностью накопления заряда, то есть его величиной ёмкости:

 ,

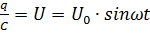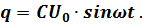
Так как ток является первой производной от заряда, то можно определить, по какой формуле его можно вычислить, найдя производную с последней формулы:  .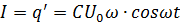

В данном случае сила тока описывается законом косинуса в то время, как значение напряжения и заряда можно описать законом синуса. Это значит, что функции находятся в противоположной фазе и имеют аналогичный вид на графике.

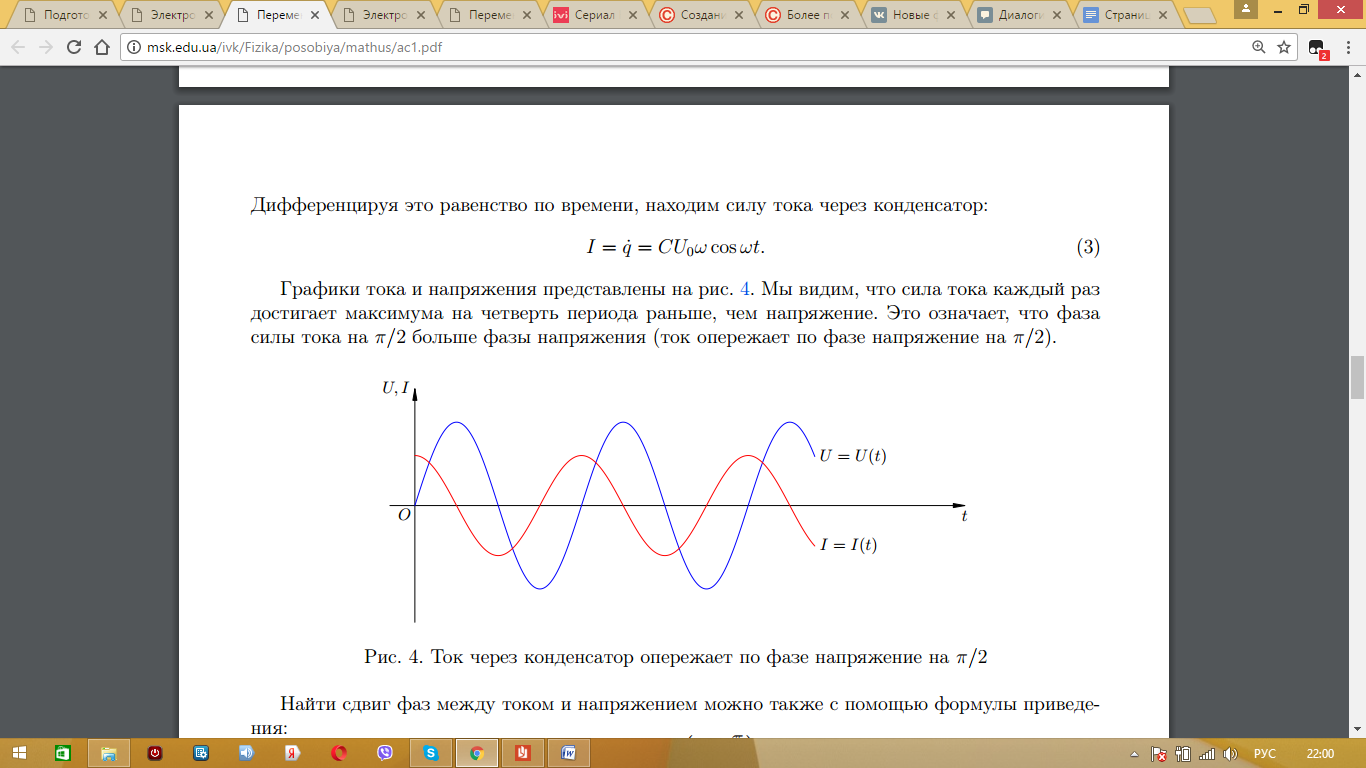
Максимальное значение силы тока будет:  .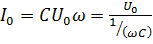

Емкостное сопротивление на конденсаторе равно  .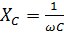

При увеличении емкостного сопротивления, амплитудное значение тока падает. Обратите внимание, в данной цепи использование закона Ома уместно только в том случае, когда необходимо определить максимальное значение тока, определить ток в любой момент времени по данному закону нельзя из-за разности фаз напряжения и силы тока.

Катушка в цепи.

Рассмотрим цепь, в которой имеется катушка. Представим, что она не имеет активного сопротивления. В таком случае, казалось бы, ничего не должно препятствовать движению тока. Однако это не так. Все дело в том, что при прохождении тока через катушку начинает возникать вихревое поле, которое препятствует прохождению тока в результате образования тока самоиндукции. Сила тока принимает следующее значение: .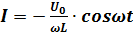

Снова можно заметить, что ток изменяется по закону косинуса, поэтому для данной цепи справедлив сдвиг фаз, который можно заметить и на графике:

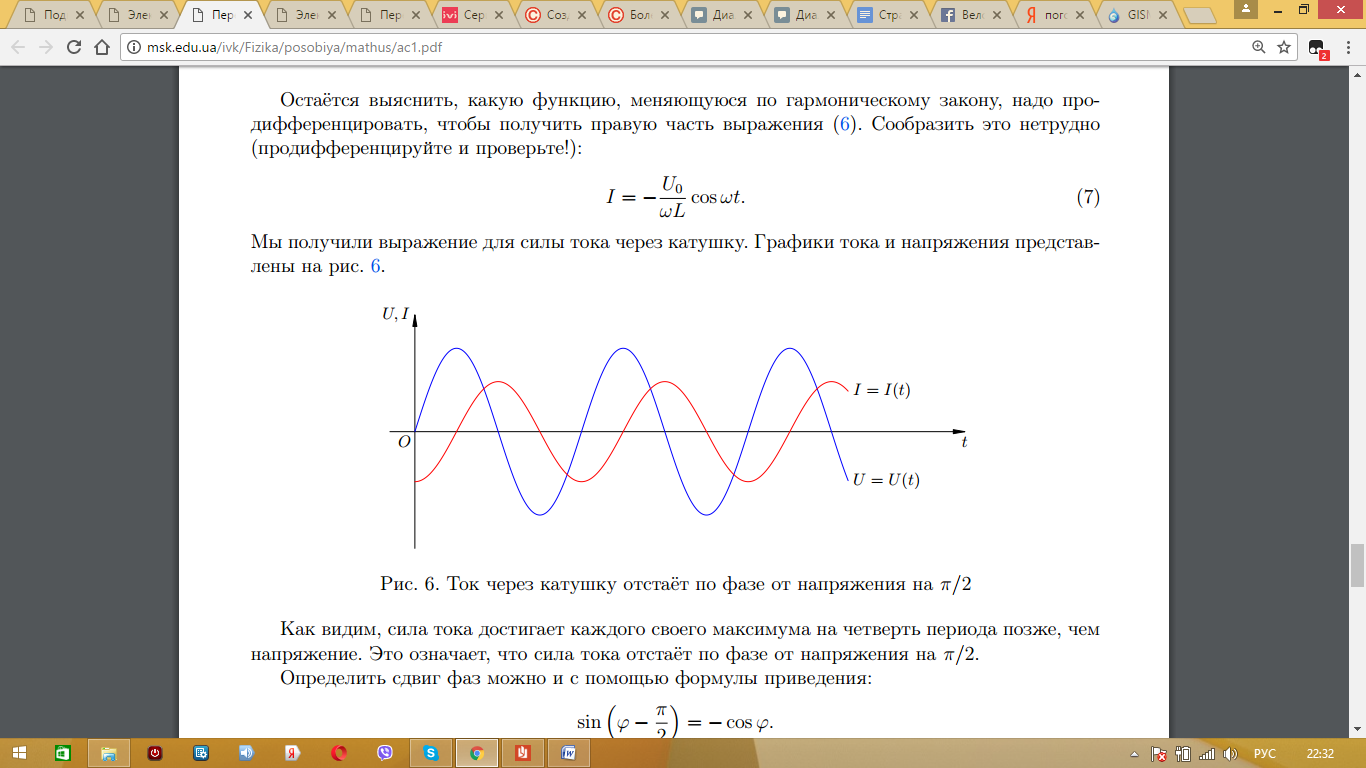
Отсюда максимальное значение тока:  .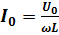

Индуктивное сопротивление цепи равно  .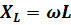

Чем больше индуктивное сопротивление, тем меньшее значение имеет амплитуда тока.