Электрические цепи даже в обыкновенной комнате имеют достаточно сложное строение. Такие цепи называются цепями со смешанным соединением. Любое сложное соединение можно разбить на части только с последовательным или параллельным соединением. В электрической цепи имеется огромное количество различных приборов, а также других составных частей. Однако при рассмотрении любого участка нам необходимо знать величины основных физических величин. Через любую часть цепи проходит определенная сила тока, имеется некоторое значение напряжения, а также всегда есть сопротивление. Именно поэтому участки с сопротивлением обозначаются следующим образом, и называются резисторами:
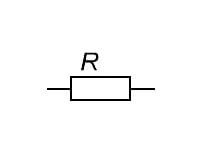
Напряжением на данном резисторе считают изменение потенциалов на входе и выходе из резистора. Как известно, в электрической цепи ток направлен от полюса "+" к полюсу "-", именно поэтому потенциал на входе в резистор всегда больше, чем потенциал на выходе. Вот эта разница и приводит к падению напряжения на данном участке.
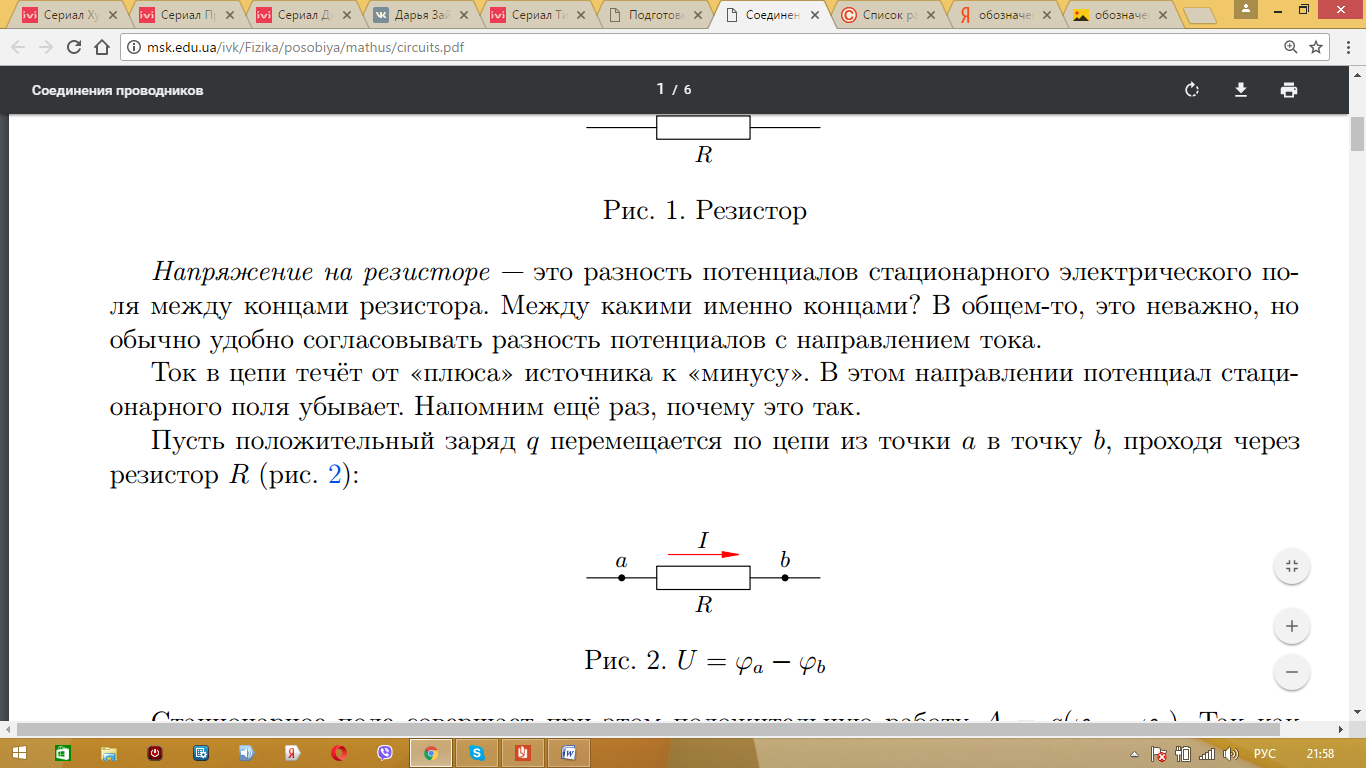
При рассмотрении любой цепи в школьном курсе физики пользуются упрощенной схемой - считается, что сопротивление на проводах нулевое и напряжение на них не падает. Но мы знаем, что у каждого вещества, из которого состоит проводник, имеется сопротивление.
Последовательное соединение. При данном виде соединения концы одного участка цепи присоединяются к началу другого участка. Свойства последовательного соединения:
1. На каждом участке цепи сила тока одинакова. Из-за того, что не происходит никакого разветвления, при одинаковом поперечном сечении проводников, за одинаковое время проходит одинаковое количество электронов. I = const .
2. Напряжение во всей цепи равно сумме напряжений на каждом участке. Так как напряжение - это величина, которая характеризуется работой, необходимой для перемещения заряда, то общая работа равна сумме работ на участках: 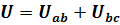 .
.
3. Для нахождения общего сопротивления, сопротивления всех участков следует сложить: 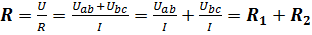 .
.
Все изложенные свойства не зависят от количества участков цепи - их может быть больше двух. В данном случае в формуле увеличится количество слагаемых напряжений и сопротивлений.

Параллельное соединение. При данном соединении начала всех резисторов соединяются в одной точке, а концы - в другой.

Узел – это точка, в которой соединены участки цепи. На данной схеме узлы обозначены буквами а и б. Свойства параллельного соединения:
1. На каждой ветке наблюдается одинаковое значение падения напряжения. U = const
2. Как известно, ток идет по той цепи, где имеется меньшее сопротивление, поэтому по каждой ветви будет проходить различная величина силы тока, в зависимости от сопротивления. Сила тока во всей цепи равна сумме сил тока на ветвях: 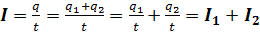 .
.
3. Для нахождения сопротивления всей цепи следует воспользоваться следующей формулой: 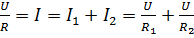 . Сократим на U и получим:
. Сократим на U и получим: 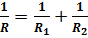 . Если из данного соотношения вывести прямую формулу для нахождения общего сопротивление, то получим:
. Если из данного соотношения вывести прямую формулу для нахождения общего сопротивление, то получим: 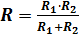 .
.
Если рассматриваемая цепь состоит из конечного количества резисторов с одинаковым сопротивлением, то для нахождения общего сопротивления следует значение одного сопротивления разделить на количество резисторов в цепи: 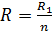 . Можно сделать вывод: при параллельном соединении общее значение сопротивления уменьшается.
. Можно сделать вывод: при параллельном соединении общее значение сопротивления уменьшается.
Закон Джоуля-Ленца.
Счетчики электроэнергии в домах измеряют величину работы тока. Рассмотрим некоторый участок цепи, через который проходит ток. Он имеет некоторое падение напряжений, сопротивление и величину силы тока. Из основной формулы нахождения напряжения можно получить величину работы тока, которая будет равна произведению заряда на падение напряжения. Совместим формулы работы с формулой для нахождения заряда, получим: 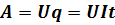 . В тот момент, когда ток протекает по цепи, происходит выделение тепла, совершается работа, а также протекают некоторые химические реакции. Используя закон Ома, можно получить несколько формул для нахождения работы:
. В тот момент, когда ток протекает по цепи, происходит выделение тепла, совершается работа, а также протекают некоторые химические реакции. Используя закон Ома, можно получить несколько формул для нахождения работы: 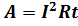 или
или 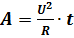 .
.
Во время протекания тока, выделяется некоторое количество тепла. То есть можно предположить, что вся работа тока идет на выделение энергии. Следовательно А = Q. Таким образом, для определения количества теплоты, которое выделяется при прохождении тока можно воспользоваться следующими формулами, которые описывают закон Джоуля-Ленца:
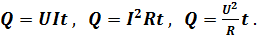
Так как мощность и работа - это две величины, тесно связанные друг с другом, то из, полученных в предыдущем параграфе, формул можно вывести мощность. Мощность характеризует скорость выполнения работы. 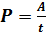 . Также можно воспользоваться и другими формулами для определения мощности:
. Также можно воспользоваться и другими формулами для определения мощности: 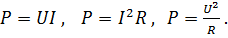
Дата: 2019-07-31, просмотров: 442.