По оптическому волокну передается не просто световая энергия, но также полезный информационный сигнал. Импульсы света, последовательность которых определяет информационный поток, в процессе распространения расплываются. При достаточно большом уширении импульсы начинают перекрываться, так что становится невозможным их выделение при приеме.

Дисперсия[1] - уширение импульсов – имеет размерность времени и определяется как квадратичная разность длительностей импульсов на выходе и входе кабеля длины L по формуле 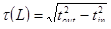. Обычно дисперсия нормируется в расчете на 1 км, и измеряется в пс/км. Дисперсия в общем случае характеризуется тремя основными факторами, рассматриваемыми ниже:

1. различие скоростей распространения направляемых мод (межмодовой дисперсией t_mod),

2. направляющими свойствами световодной структуры (волноводной дисперсией t_w),

3. свойствами материала оптического волокна (материальной дисперсией t_mat).

Рис. 4.6. Виды дисперсии.

Чем меньше значение дисперсии, тем больший поток информации можно передать по волокну. Результирующая дисперсия t определяется из формулы:

     (4-13)

Межмодовая дисперсия.

Межмодовая дисперсия возникает вследствие различной скорости распространения у мод, и имеет место только в многомодовом волокне. Для ступенчатого многомодового волокна и градиентного многомодового волокна с параболическим профилем показателя преломления ее можно вычислить соответственно по формулам:

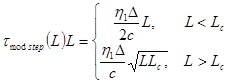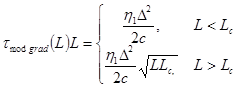, , (4-14), (4-15)

где L_с – длина межмодовой связи (для ступенчатого волокна порядка 5 км, для градиентного – порядка 10 км).

Изменение закона дисперсии с линейного на квадратичный связано с неоднородностями, которые есть в реальном волокне. Эти неоднородности приводят к взаимодействию между модами, и перераспределению энергии внутри них. При L>L_c наступает установившейся режим, когда все моды в определенной установившейся пропорции присутствуют в излучении. Обычно длины линий связи между активными устройствами при использовании многомодового волокна не превосходят 2 км и значительно меньше длины межмодовой связи. Поэтому можно пользоваться линейным законом дисперсии.

Вследствие квадратичной зависимости от D значения межмодовой дисперсии у градиентного волокна значительно меньше, чем у ступенчатого, что делает более предпочтительным использование градиентного многомодового волокна в линиях связи.

На практике, особенно при описании многомодового волокна, чаще пользуются термином полоса пропускания. При расчете полосы пропускания W можно воспользоваться формулой :

W=0,44/t                                                                         (4-16)

Измеряется полоса пропускания в МГц км. Из определения полосы пропускания видно, что дисперсия накладывает ограничения на дальность передачи и верхнюю частоту передаваемых сигналов. Физический смысл W – это максимальная частота (частота модуляции) передаваемого сигнала при длине линии 1 км. Если дисперсия линейно растет с ростом расстояния, то полоса пропускания зависит от расстояния обратно пропорционально.

Хроматическая дисперсия.

Хроматическая дисперсия состоит из материальной и волноводной составляющих и имеет место при распространении как в одномодовом, так и в многомодовом волокне. Однако наиболее отчетливо она проявляется в одномодовом волокне из-за отсутствия межмодовой дисперсии.

Материальная дисперсия обусловлена зависимостью показателя преломления волокна от длины волны. В выражение для дисперсии одномодового волокна входит дифференциальная зависимость показателя преломления от длины волны:

                           (4-17)

Волноводная дисперсия обусловлена зависимостью коэффициента распространения моды от длины волны:

,                              (4-18)

где ведены коэффициенты М(l) и N(l) удельные материальная и волноводная дисперсии соответственно, а Dl (нм) – уширение длины волны вследствие некогерентности источника излучения. Результирующее значение коэффициента удельной хроматической дисперсии определяется как D(l)=М(l)+N(l). Удельная дисперсия имеет размерность пс/(нм км). Если коэффициент волноводной дисперсии всегда больше нуля, то коэффициент материальной дисперсии может быть как положительным, так и отрицательным. И здесь важным является то, что при определенной длине волны (примерно 1310±10 нм для ступенчатого одномодового волокна) происходит взаимная компенсация М(l) и В, а результирующая дисперсия D(l) обращается в ноль. Длина волны, при которой это происходит, называется длиной волны нулевой дисперсии l₀. Обычно указывается некоторый диапазон длин волн, в пределах которых может варьироваться l₀ для данного конкретного волокна.

Фирма Corning использует следующий метод определения удельной хроматической дисперсии. Измеряются задержки по времени при распространении коротких импульсов света в волокне длиной не меньше 1 км. После получения выборки данных для нескольких длин волн из диапазона интерполяции (800-1600 нм для MMF, 1200-1600 для SF и DSF) делается повторная выборка измерения задержек на тех же длинах волн, но только на коротком эталонном волокне (длина 2 м). Времена задержек, полученных на нем, вычитаются из соответствующих времен, полученных на длинном волокне.

Для одномодового ступенчатого и многомодового градиентного волокна используется эмпирическая формула Селмейера: t(l)=А+Вl²+Сl^-2. Коэффициенты А,В,С являются подгоночными, и выбираются так, чтобы экспериментальные точки лучше ложились на кривую t(l). Тогда удельная монохроматическая дисперсия вычисляется по формуле:

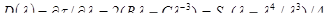                      (4-19)

где l₀=(С/В)^1/4 – длина волны нулевой дисперсии, новый параметр S₀=8B – наклон нулевой дисперсии (размерность пс/(нм² км), а l - рабочая длина волны, для которой определяется удельная хроматическая дисперсия.

Для волокна со смещенной дисперсией эмпирическая формула временных задержек записывается в виде t(l)=А+Вl+Сllnl, а соответствующая удельная дисперсия определяется как

                          (4-19)

со значениями параметров l₀=е^-(1+В/С) и S₀=C/l₀, где l - рабочая длина волны, l₀ – длина волны нулевой дисперсии, и S₀ – наклон нулевой дисперсии.

Хроматическая дисперсия связана с удельной хроматической дисперсией простым соотношением t_chr(l)=D(l)Dl, где Dl - ширина спектра излучения источника. К уменьшению хроматической дисперсии ведет использование более когерентных источников излучения, например лазерных передатчиков (Dl@2 нм), и использование рабочей длины волны более близкой к длине волны нулевой дисперсии. В табл. 4.3. представлены дисперсионные свойства различных оптических волокон.

Табл. 4.3. Дисперсия оптических сигналов в различных оптических волокнах.

Тип волокна

L , нм

Межмодовая дисперсия, пс/км

t _mod