Относительная разность показателей преломления. Волокно состоит из сердцевины и оболочки. Оболочка окружает оптически более плотную сердцевину, являющуюся светонесущей частью волокна. Будем обозначать через n1 и n2 показатели преломления сердцевины и оболочки соответственно. Один из важных параметров, который характеризует волокно, - это относительная разность показателей преломления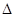 
:
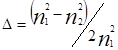. (4 – 1)
Если показатель преломления оболочки выбирается всегда постоянной величиной, то показатель преломления сердцевины в общем случае может зависеть от радиуса. Распространение света по волокну можно объяснить на основе принципа полного внутреннего отражения, вытекающего из закона преломления света Снеллиуса:
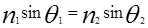, (4 –2)
где n1 – показатель преломления среды 1, - угол падения, n2 – показатель преломления среды 2,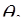 
- угол преломления.
Формальные выкладки удобнее производить для ступенчатого волокна, в котором показатель преломления сердцевины является постоянной величиной (n1 = const). Так как сердцевина является оптически более плотной средой по отношению к оболочке (n1 > n2), то существует критический угол падения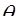 
- внутренний угол падения на границу, при котором преломленный луч идет на границе двух сред ( 
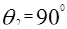). Из закона Снеллиуса легко найти этот критический угол падения:
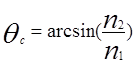(4-3)
Если угол падения на границу раздела меньше критического угла падения (луч 2), то при каждом внутреннем отражении от границы вся энергия возвращается обратно в сердцевину благодаря полному внутреннему отражению.
Лучи, траектории которых полностью лежат в оптически более плотной среде, называются направляемыми. Поскольку энергия таких лучей не рассеивается наружу, они могут распространяться на большие расстояния.
Числовая апертура. Важным параметром, характеризующим волокно, является числовая апертура NA. Она связана с максимальным углом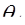 
вводимого в волокно излучения из свободного пространства, при котором свет испытывает полное внутреннее отражение и распространяется по волокну, формулой:
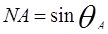(4 – 4)
Фирмы-изготовители волокна экспериментально измеряют угол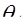 
и указывают соответствующее значение числовой апертуры для каждого поставляемого типа волокна. Для волокна со ступенчатым профилем легко получить значение числовой апертуры, выраженное через показатели преломления:
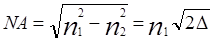(4 – 5)
Для градиентного волокна используется понятие локальной числовой апертуры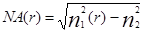 
, значение которой максимально на оси и падает до 0 на границе сердцевины и оболочки. Для градиентного волокна с параболическим показателем преломления, формула ХХХ, определяется эффективная числовая апертура, которая равна
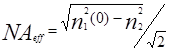(4 – 6)
где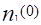 
- максимальное значение показателя преломления на оси.
Нормированная частота. Другим важным параметром, характеризующим волокно и распространяющийся по нему свет, является нормированная частота V, которая определяется как
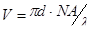(4 – 5)
где d - диаметр сердцевины волокна.
Номенклатура мод. При более строгом рассмотрении процесса распространения света по волокну следует решать волновые уравнения Максвелла. Именно в этой трактовке лучи ассоциируются с волнами, причем различные типы волн – решения уравнений – называются модами.
Сами моды обозначаются буквами E и/или H с двумя индексами n и m. Индекс n характеризует азимутальные свойства волны (число изменений поля по окружности), а m – радиальные (число изменений поля по диаметру). По оптическому волокну распространяются только два типа волн: симметричные (E0m и H0m), у которых только одна продольная составляющая, и несимметричные (смешанные) (Enm и Hnm), у которых две продольные составляющие.
При этом, если преобладает продольная составляющая электрического поля – Еz, то волна обозначается ЕНnm, а если преобладает продольная составляющая магнитного поля Нz, то волна называется , то волна называется НЕnm, Сопоставляя волновую теорию с геометрической оптикой, следует отметить, что симметричные моды Е0m и Н0m соответствуют меридиональным лучам, несимметричные моды Еnm и Нnm – косым лучам.
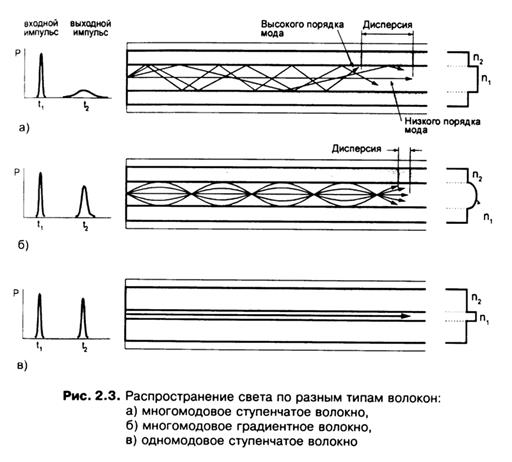
По волокну могут распространятся как только одна мода – одномодовый режим, так и много мод – многомодовый режим. Многомодовый или одномодовый характер идущего по волокну света коренным образом влияет на дисперсию, а следовательно, и на пропускную способность волокна. Расчет на основе уравнений Максвелла позволяет найти простой критерий распространения одной моды: V<2,405 (точное значение константы в правой части неравенства определяется первым нулем функции Бесселя I0(x)). Это гибридная мода НЕ11. Отметим, что нормированная частота явно зависит от длины волны света. В табл. 4.1 приведены значения нормированной частоты, вычесленные по формуле (4-7).
Как видно из табл. (4.1), в одномодовом ступенчатом волокне при длине волны света 1550 нм выполняется критерий (4-8), и поэтому распространяется только одна мода. При длине волны 1310 нм критерий не выполнен, что означает возможность распространения нескольких мод в одномодовом волокне на этой длине волны. На практике, однако, волокно помещается в кабель, который, будучи проложенным, имеет множество изгибов. Особенно велики искривления волокна в сплайс-боксах. Искривления волокна приводит к быстрому затуханию неосновных мод. Во всех остальных случаях наблюдается многомодовый характер распространения света. Отметим, что при длине волны 850 нм критерий (4-8) нарушается для всех типов волокон. Таким образом, если вводить излучение длинной волны 850 нм в одномодовое волокно, то иметь место будет многомодовый режим распространения света. Противоречия здесь нет. Дело в том, что ступенчатое одномодовое волокно 8/125 предназначено для использования в спектральных окрестностях двух длин волн: 1310 нм и 1550 нм, где оно в истинном смысле проявляет себя как одномодовое.
Таблица (4.1). Значения основных оптических параметров волокон и нормированной частоты V для различных длин волн.
| №№ | ||||
Оптическое волокно
l (нм)
Обозначения: step MMF (multi mode fiber) – ступенчатое многомодовое волокно;
step SMF (single mode fiber) – ступенчатое одномодовое волокно;
grad MMF – градиентное многомодовое волокно;
1. - параметры волокон
** - параметры волокон, производимых фирмой Corning
Количество мод. Если при V<2,405 может распространятся только одна мода, то с ростом v количество мод начинает резко расти, причем новые типы мод «включаются» при переходе v через определенные критические значения, табл. 4.2
Таблица 4.2. Номенклатура мод низких порядков.
| Нормированная частота V | Числомод Nm | Тип мод |
| 0-2б405 | 1 | НЕ11 – основная мода (единственно допустимая для одномодового волокна |
| 2,405-3,832 | 4 | НЕ11, Н01, Е01, НЕ21 |
| 3,832-5,136 | 7 | НЕ11, Н01, Е01, НЕ21, НЕ12, ЕН11, НЕ31 |
| 5,136-5,52 | 9 | НЕ11, Н01, Е01, НЕ21, НЕ12, ЕН11, НЕ31, ЕН21, НЕ41 |
| 5,52-6,38 | 12 | НЕ11, Н01, Е01, НЕ21, НЕ12, ЕН11, НЕ31, ЕН21, НЕ41, Н02, Е02, НЕ22 |
| 6,38-7,02 | 14 | НЕ11, Н01, Е01, НЕ21, НЕ12, ЕН11, НЕ31, ЕН21, НЕ41, Н02, Е02, НЕ22, ЕН31, НЕ51 |
| 7,02-7,59 | 17 | НЕ11, Н01, Е01, НЕ21, НЕ12, ЕН11, НЕ31, ЕН21, НЕ41, Н02, Е02, НЕ22, ЕН31, НЕ51, НЕ13, ЕН12, НЕ31 |
| 7,59-8,42 | 19 | НЕ11, Н01, Е01, НЕ21, НЕ12, ЕН11, НЕ31, ЕН21, НЕ41, Н02, Е02, НЕ22, ЕН31, НЕ51, НЕ13, ЕН12, НЕ31, ЕН41, НЕ61 |
При больших значениях V количество мод Nm для ступенчатого волокна можно оценить по формуле:
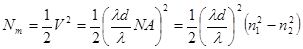(4-8)
Значение этого выражения может быть как целым, так и дробным. В действительности же число мод может быть только целым и составлять величину от одной до нескольких тысяч.
Количество мод для градиентного оптического волокна с параболическим профилем сердцевины:
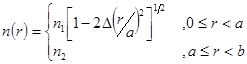(4-9)
(a – радиус сердцевины, b – радиус оболочки) определяется так:
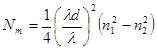(4-10)
Дата: 2019-07-31, просмотров: 225.
