Содержание
Введение3
Исходные данные4
1. Расчет параметров зубчатой передачи и основных размеров5
2. Расчет активного слоя якоря
2.1 Расчет параметров обмотки
2.2 Параметры обмотки якоря
3. Расчет щеточно-коллекторного узла
3.1 Выбор числа и размера щеток
3.2 Определение рабочей длины коллектора
4. Расчет магнитной цепи
4.1 Сердечник якоря
4.2 Главные полюса
4.3 Остов
4.4 Участок сердечника якоря
4.5 Участок зубцового слоя якоря
4.6 Участок сердечника главного полюса
4.7 Участок стыка полюса с остовом
4.8 Участок выхода потока из полюса в остов
4.9 Ярмо остова
4.10 Расчет воздушного зазора
4.11 Расчет конструкционных размеров и параметров катушки
главного полюса
5. Расчет стационарной коммутации
6. Расчет добавочных полюсов
Список использованных источников
Введение
В настоящее время совершенствование электроподвижного состава является одним из главных направлений в развитии железнодорожного транспорта и остается таковым в ближайшей перспективе. Развитие средств электроники и микропроцессорной техники способствует появлению принципиально новых по своим техническим возможностям локомотивов с высоким уровнем автоматизации процессов управления. Однако каковы бы ни были масштабы внедрения новых средств автоматизированного контроля и управления техническими системами электрических локомотивов, их реализуемые эксплуатационные качества всегда будут определяться техническими возможностями их движителей – тяговых электродвигателей (ТЭД).
В этих условиях исключительно важная роль отводится процессу проектирования тяговых электродвигателей. В ходе разработки новой конструкции приходиться неоднократно уточнять и тщательно увязывать мужду собой множество размеров и параметров машины для одновременного учета и выполнения многочисленных конструкторских, технологических, экономических требований и ограничений.
В данном курсовом проекте основное внимание уделено вопросам разработки конструкции основных частей машины и их взаимосвязи в единой системе тягового двигателя. Необходимо отметить, что в своей основе методика проектирования тягового электрического двигателя, опирается на традиционную методику проектирования тяговых машин, разработанную и используемую в настоящее время коллективами проектировщиков отечественного электровозостроения.
Исходные данные
Номинальная мощность двигателя P 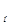 = 145 кВт;
= 145 кВт;
Номинальное напряжение питания двигателя U 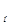 = 1500 В;
= 1500 В;
Корпусное напряжение U 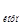 = 3000 В;
= 3000 В;
Номинальная скорость движения локомотива V 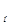 = 48 км/ч;
= 48 км/ч;
Конструкционная скорость движения локомотива V 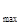 = 98 км/ч;
= 98 км/ч;
Номинальный коэффициент регулирования возбуждения β 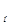 = 0,43;
= 0,43;
Диаметр бандажей ведущих колес D 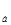 = 1,05 м;
= 1,05 м;
Диаметр оси колесной пары d 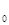 = 180 мм;
= 180 мм;
Вид торможения рекуперативное;
Вид системы вентиляции машины самовентиляция;
Род тока постоянный;
Вид локомотива МВПС;
Тип подвешивания двигателя опорно - рамное;
Класс изоляции “B”.
Расчет активного слоя якоря
Расчет параметров обмотки
Общее число проводников обмотки якоря
N = 2 · K, (2.1)
N = 2 · 306 = 612 проводников.
Ток якоря в номинальном режиме
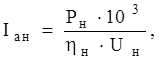 (2.2)
(2.2)
где hн – КПД двигателя. Принимаю hн = 0,91, согласно [1].
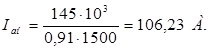
Выбираем простую петлевую обмотку якоря, у которой 2а = 2р.
Линейная токовая нагрузка якоря
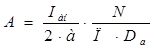 , (2.3)
, (2.3)
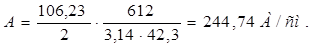
Ток параллельной ветви
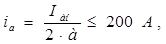 (2.4)
(2.4)
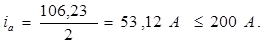
При определении рационального числа пазов Z учитывается ограничение по условиям нагрева пучка проводников в пазу якоря в виде величины объема тока в пазу
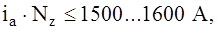 (2.5)
(2.5)
где Nz – число проводников в одном пазу. Принимаю Nz = 2 uk = 12.
53,12 · 12 = 637,44 А 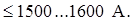
Неравенство (2.5) выполняется.
Число пазов якоря находится по формуле
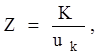 (2.6)
(2.6)
где uk – число коллекторных пластин на паз. Принимаю uk = 6.
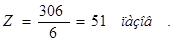
Первый шаг обмотки в реальных пазах должен удовлетворять условию
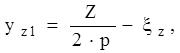 (2.7)
(2.7)
где 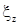 – укорочение шага обмотки якоря в реальных пазах.
– укорочение шага обмотки якоря в реальных пазах.
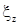 = 0,5 паза при петлевой обмотке.
= 0,5 паза при петлевой обмотке.
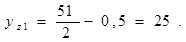
Произведем окончательную увязку между собой числа пазов Z, проводников N и коллекторных пластин К, которая должна обеспечивать выполнение требования внутренней симметрии обмотки якоря
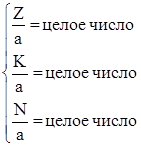 , (2.8)
, (2.8)
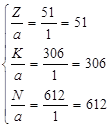 .
.
Найдем допустимое значение плотности тока в проводниках якоря
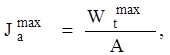 (2.9)
(2.9)
где Wtmax – допустимый предел теплового фактора машины.
Принимаю Wtmax = 2050 согласно [1].
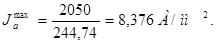
Расчетная величина Ja не должна превышать (5…6) А/мм2.
Принимаю Ja = 6 А/мм2.
Наметим площадь поперечного сечения активного проводника якоря
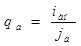 , (2.10)
, (2.10)
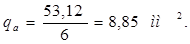
По значению qа намечаем размеры проводника hпр × bпр.
По ГОСТ 434-53, приложение А согласно [1], выбираю проводник с размерами
hпр × bпр = 1,4 × 6,7 qпр = 9,165 мм2. (2.11)
Уточним допустимое значение плотности тока в проводниках якоря
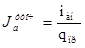 , (2.12)
, (2.12)
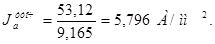
Проведем проверку правильности выбора сечения проводника
A · ja < 2050 A, (2.13)
244,74 · 5,796 = 1418,51 А < 2050 A.
Неравенство (2.13) выполняется.
Высоту паза якоря находим по выражению
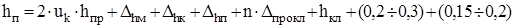 , (2.14)
, (2.14)
где Dпрокл – толщина изоляционных прокладок Dпрокл = 0,5 мм;
nпрокл – число прокладок. nпрокл = 3;
hкл – высота клина. hкл = 4 мм;
nкорп – число слоев корпусной изоляции. nкорп =6;
Dhм – толщина межвитковой изоляции по высоте паза якоря;
Dhк – толщина корпусной изоляции по высоте паза якоря;
Dhп – толщина покровной изоляции по высоте паза якоря;
(0,2…0,3) – зазор на укладку секций в паз;
(0,15…0,2) – разница между размером паза в свету и размером паза в
штампе.
Принимаю: 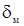 = 0,1 мм,
= 0,1 мм, 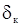 = 0,1 мм,
= 0,1 мм, 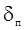 = 0,1мм.
= 0,1мм.
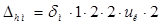 , (2.15)
, (2.15)
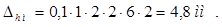
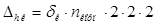 , (2.16)
, (2.16)
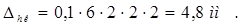
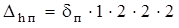 , (2.17)
, (2.17)
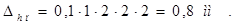
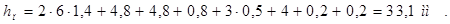
Ширину паза якоря вычисляем по формуле
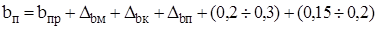 , (2.18)
, (2.18)
где Dbм – толщина межвитковой изоляции по ширине паза якоря;
Dbк – толщина корпусной изоляции по ширине паза якоря;
Dbп – толщина покровной изоляции по ширине паза якоря;
(0,2…0,3) – зазор на укладку секций в паз;
(0,15…0,2) – разница между размером паза в свету и размером паза.
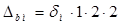 , (2.19)
, (2.19)
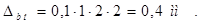
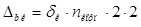 , (2.20)
, (2.20)
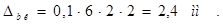
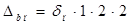 , (2.21)
, (2.21)
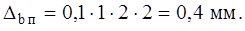
Найдем ширину паза якоря
bп = 6,7 + 0,4 + 2,4 + 0,4 + 0,2 + 0,2 = 10,3 мм.
Полученные размеры паза якоря должны удовлетворять следующим условиям:
– bп = 10,3 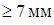 – удовлетворяет;
– удовлетворяет;
– hп = 33,1 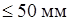 – удовлетворяет.
– удовлетворяет.
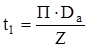 , (2.22)
, (2.22)
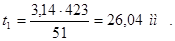
Ширина зубца на поверхности якоря bz1
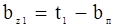 , (2.23)
, (2.23)
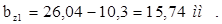
Шаг по пазам в расчетном сечении tz1/3 (на высоте 1/3hп )
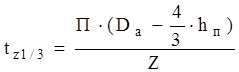 , (2.24)
, (2.24)
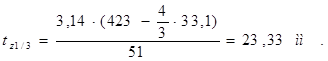
Ширина зубца в расчетном сечении bz1/3
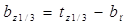 , (2.25)
, (2.25)
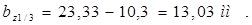
Шаг по дну пазов
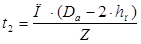 , (2.26)
, (2.26)
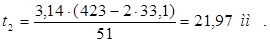
Ширина зубца у основания bz2
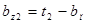 , (2.27)
, (2.27)
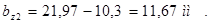
Необходимо проконтролировать, чтобы выполнялось условие
bz2 ³ 7 мм, для обеспечения достаточной механической прочности зубца.
Магнитный поток находим по выражению
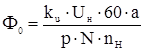 , (2.28)
, (2.28)
где ku – коэффициент, учитывающий потери напряжения на внутренних
сопротивлениях обмоток двигателя.
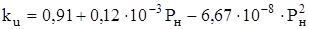 , (2.29)
, (2.29)
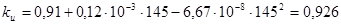 .
.
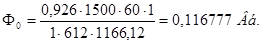
Далее определяем длину шихтованного пакета якоря
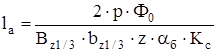 , (2.30)
, (2.30)
где Вz1/3 – индукция в зубцах якоря. Принимаю Вz1/3 = 1,8 Тл;
ad – расчетный коэффициент полюсного перекрытия, для машины без
компенсационной обмоткой. Принимаю ad = 0,64;
Кс – коэффициент заполнения пакета сталью. Принимаю Кс = 0,97.
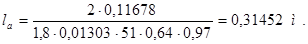
la 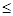 315 мм при опорно-рамном подвешивании и односторонней зубчатой передаче, что удовлетворяет условию.
315 мм при опорно-рамном подвешивании и односторонней зубчатой передаче, что удовлетворяет условию.
Параметры обмотки якоря
Выбрав тип обмотки и геометрию активного слоя якоря, устанавливаю шаги обмотки якоря.
Результирующий шаг обмотки в элементарных пазах или шаг по коллектору в коллекторных делениях при простой петлевой обмотке
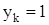 . (2.31)
. (2.31)
Первый шаг в коллекторных делениях
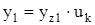 , (2.32)
, (2.32)
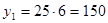 .
.
Второй шаг в коллекторных делениях для простой петлевой обмотки
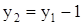 , (2.33)
, (2.33)
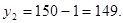 .
.
Укорочение обмотки в коллекторных делениях
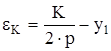 , (2.34)
, (2.34)
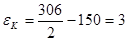 .
.
Полюсное деление по окружности якоря
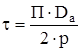 , (2.35)
, (2.35)
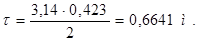
Длина передних и задних лобовых участков якорных проводников
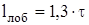 , (2.36)
, (2.36)
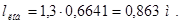 .
.
Длина полувитка обмотки якоря
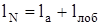 , (2.37)
, (2.37)
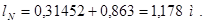
Общая длина проводников обмотки якоря
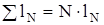 . (2.38)
. (2.38)
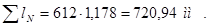
Сопротивление обмотки якоря при 20˚С
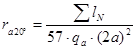 , (2.39)
, (2.39)
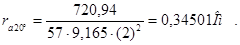
Масса меди обмотки якоря
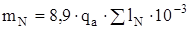 , (2.40)
, (2.40)
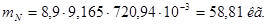
Выбор числа и размера щеток
Ток, протекающий через щетку, находим по формуле
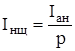 , (3.1)
, (3.1)
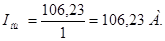
Определим требуемую площадь щеточного контакта одного щеткодержателя
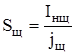 , (3.2)
, (3.2)
где jщ – плотность тока под щеткой.
Допустимую плотность тока назначаем по выбранной марке щеток, согласно[1]. Выбираю марку ЭГ51.
Принимаю jщ =12 А/см2.
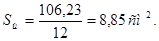
Максимально-допустимая ширина щетки
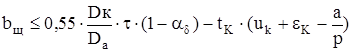 , (3.3)
, (3.3)
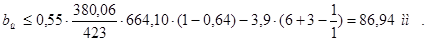
По ГОСТ 8611-57, согласно [1], выбираю ширину щетки и принимаю ее равной 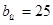 мм.
мм.
Далее рассчитываю длину щеточного контакта
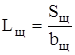 , (3.4)
, (3.4)
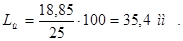
Принимаю nщ = 1 – число элементарных щеток по длине коллектора.
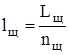 , (3.5)
, (3.5)
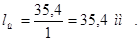
Ориентируясь по ГОСТ 8611-57, согласно[1], выбираю составной тип конструкции щеток и принимаю длину одной щетки lщ = 40 мм.
Окончательная величина площади щетки Sщ
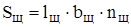 , (3.6)
, (3.6)
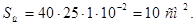
Тогда точное значение плотности тока под щеткой
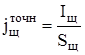 , (3.7)
, (3.7)
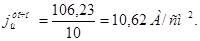
Расчет магнитной цепи
Сердечник якоря
Определяем высоту сечения ярма якоря
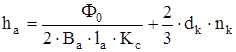 , (4.1)
, (4.1)
где 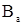 – индукция в сердечниках якоря. Принимаем
– индукция в сердечниках якоря. Принимаем 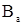 =1,8 Тл;
=1,8 Тл;
dк – диаметр вентиляционных каналов. Принимаем dк = 0,02 м;
nк – число рядов вентиляционных каналов. nк = 1.
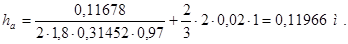
Внутренний диаметр сердечника якоря
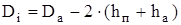 , (4.2)
, (4.2)
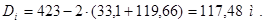
Диаметр вала двигателя в его средней части при односторонней передаче
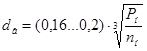 , (4.3)
, (4.3)
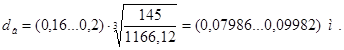
Принимаю 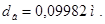
Поскольку внутренний диаметр Di не совпадает с диаметром вала, решается вопрос о том, какой элемент будет сопрягающим между шихтованным телом якоря и валом двигателя
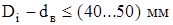 , (4.4)
, (4.4)
117,48 – 99,82 = 17,66 мм.
т.е. устанавливают сплошную втулку якоря.
Ширина полюсного башмака
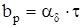 , (4.5)
, (4.5)
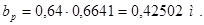
Длина сердечника полюса
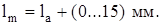 (4.6)
(4.6)
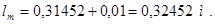
Главные полюса
Площадь поперечного сечения сердечника главного полюса
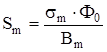 , (4.7)
, (4.7)
где 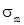 – коэффициент рассеяния обмоток главных полюсов.
– коэффициент рассеяния обмоток главных полюсов. 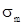 = 1,05;
= 1,05;
Bm – индукция в сердечнике полюса. Bm 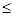 (1,4…1,7) Тл.
(1,4…1,7) Тл.
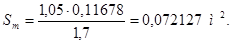
Ширина сердечника главного полюса
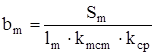 , (4.8)
, (4.8)
где kmсm – коэффициент заполнения сталью сердечника. kmсm= 0,97;
kср – коэффициент подреза углов сердечника полюса для лучшего
вписывания катушки возбуждения. При намотке меди на широкое
ребро kср= 1.
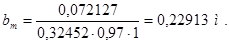
Сечение аb в основании рога полюса должно быть достаточным для прохождения магнитного потока к крайним участкам полюсного наконечника, для этого должно выполняться условие
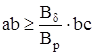 , (4.9)
, (4.9)
где 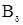 – индукция в воздушном зазоре;
– индукция в воздушном зазоре;
Bр – допустимая индукция в основании рога полюса;
ab, bc – размеры снимаемые с эскиза с учетом масштаба изображения.
Определим индукцию в воздушном зазоре
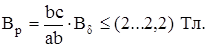 (4.10)
(4.10)
Для этого найдем индукцию в воздушном зазоре
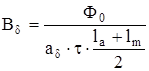 , (4.11)
, (4.11)
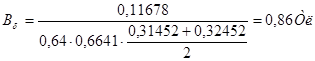
По эскизу величина ab = 19 мм, bc = 46 мм.
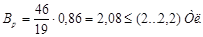
Неравенство (4.10) выполняется.
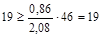 .
.
Неравенство (4.9) выполняется.
На предварительном этапе высоту полюса hm примем
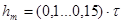 при 2р = 2, (4.12)
при 2р = 2, (4.12)
hm = 0,121 · 664,1 = 80,36 мм.
Остов
Для определения размеров остова сначала рассчитывается площадь сечения ярма остова
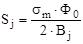 , (4.13)
, (4.13)
где 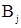 – индукция в остове.
– индукция в остове. 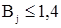 . Принимаю
. Принимаю 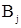 =1,4 Тл.
=1,4 Тл.
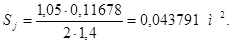
Расчетная длина ярма остова в осевом направлении при четырехгранном остове находится как наименьший из размеров.
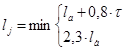 , (4.14)
, (4.14)
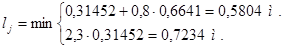
Принимаю 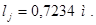
Средняя толщина остова
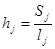 , (4.15)
, (4.15)
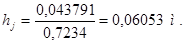
Толщина остова в месте расположения главных полюсов
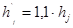 , (4.16)
, (4.16)
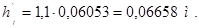
Толщина остова в месте расположения добавочных полюсов
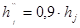 , (4.17)
, (4.17)
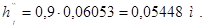
Внешний размер остова
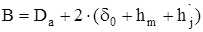 , (4.18)
, (4.18)
где 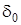 – величина воздушного зазора. Принимаем
– величина воздушного зазора. Принимаем 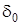 = 6 мм.
= 6 мм.
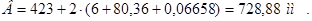
Ширина прилива под добавочным полюсом
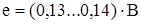 . (4.19)
. (4.19)
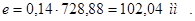
Процедура вписывания тягового двигателя в централь состоит в проверке, а при необходимости в корректировке предварительно найденных размеров магнитопровода с тем, чтобы обеспечить выполнения равенства
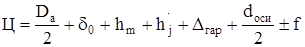 , (4.20)
, (4.20)
где 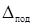 – величина гарантийного зазора.
– величина гарантийного зазора. 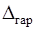 = 40 мм;
= 40 мм;
 – подрез (прилив) остова со стороны моторно-осевых подшипников.
– подрез (прилив) остова со стороны моторно-осевых подшипников.
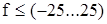 ,принимаю f= - 24,44
,принимаю f= - 24,44
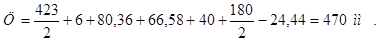
Задача вписывания габаритов двигателя по высоте состоит в нахождении такой величины t превышения оси двигателя над осью колесной пары для выбранного значения просвета С, чтобы выполнялось следующее неравенство
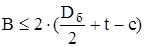 , (4.21)
, (4.21)
где с 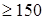 мм – гарантийный просвет. Принимаем с = 150 мм;
мм – гарантийный просвет. Принимаем с = 150 мм;
t 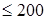 мм – ограниченная величина приподнимания вала двигателя
мм – ограниченная величина приподнимания вала двигателя
относительно оси колесной пары. Принимаем t = 20 мм.
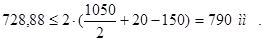
Участок сердечника якоря
Площадь поперечного сечения ярма сердечника якоря
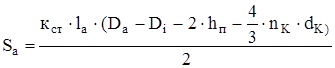 , (4.22)
, (4.22)
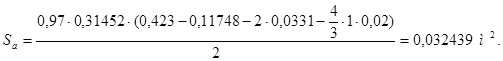
Величина магнитной индукции рассчитывается по формуле
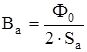 , (4.23)
, (4.23)
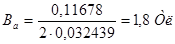
По индукции 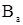 = 1,8 Тл согласно [1], из Приложения «В» находим напряженность
= 1,8 Тл согласно [1], из Приложения «В» находим напряженность 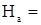 14200 А/м.
14200 А/м.
Длину магнитной линий снимаем с учетом масштаба с эскиза магнитной цепи. La = 0,1625 м.
Падение магнитных потенциалов в сердечнике якоря
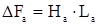 , (4.24)
, (4.24)
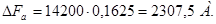
Результаты вышеприведенных и последующих расчетов сведены в таблицу 4.1.
Ярмо остова
Площадь сечения ярма остова
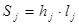 , (4.35)
, (4.35)
Sj = 0,06053 · 0,7234 = 0,043787 м2.
Индукция в остове
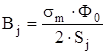 , (4.36)
, (4.36)
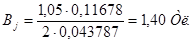
Магнитное напряжение в ярме остова
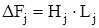 , (4.37)
, (4.37)
где Hj – магнитная напряженность в остове, согласно [1], Hj = 2010 А/м;
Lj – длина силовой линии в ярме остова, из эскиза магнитной цепи.
Lj’ = 0,644 м.
DFj = 2010∙ 0,644 = 1294,44 А.
Расчет воздушного зазора
Таблица 4.1 – Расчет магнитных напряжений и МДС возбуждения
| Номер участка | Наименование участка | Магнитный поток, Вб | Сечение, м2 | Индукция, Тл | Напряженность, А/м | Длина силовой линии, м | Магнитное напряжение, А |
| 1 | Сердечник якоря | 0,058 | 0,032439 | 1,8 | 14200 | 0,1625 | 2307,5 |
| 2 | Зубцовый слоя якоря | 0,117 | 0,064876 | 1,8 | 14200 | 0,0331 | 470,02 |
| 3 | Зубцовый слой полюса | – | – | – | – | – | – |
| 4 | Сердечник полюса | 0,123 | 0,072127 | 1,7 | 7050 | 0,12 | 846 |
| 5 | Стык полюса с остовом | – | – | – | – | – | 136 |
| 6 | Переход из полюса в остов | 0,061 | 0,036862 | 1,66 | 6800 | 0,08 | 544 |
| 7 | Ярмо остова | 0,061 | 0,043787 | 1,4 | 2010 | 0,644 | 1294,44 |
| Сумма магнитных напряжений стальных участков | 5597,96 | ||||||
| 8 | Воздушный зазор | 0,117 | 0,001947 | 0,86 | – | – | 4248,19 |
| МДС намагничивания | 9846,15 | ||||||
| МДС на компенсацию действия реакции якоря | 918,3 | ||||||
| МДС Возбуждения обмотки главного полюса | 10764,45 | ||||||
Потребная МДС воздушного зазора для обеспечения заданных свойств двигателя
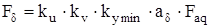 , (4.38)
, (4.38)
где 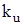 – коэффициент использования мощности.
– коэффициент использования мощности.
При 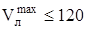 ,
, 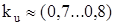 . Принимаю
. Принимаю 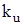 = 0,8;
= 0,8;
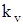 – коэффициент регулируемости по скорости;
– коэффициент регулируемости по скорости;
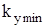 – коэффициент магнитной устойчивости;
– коэффициент магнитной устойчивости;
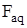 – МДС поперечной реакции якоря.
– МДС поперечной реакции якоря.
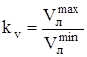 , (4.39)
, (4.39)
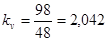 .
.
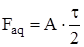 , (4.40)
, (4.40)
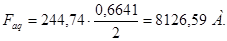
В машинах без компенсационной обмотки, для снижения воздействия поперечной реакции якоря наконечникам главных полюсов придают особую форму, так чтобы зазор расходился бы к краям полюса. Расходящиеся воздушные зазоры обеспечивают нарастание магнитного сопротивления потоку поперечной реакции якоря соответственно росту её МДС от центра главного полюса. Очевидно, что степень искажения магнитного поля главных полюсов, а значит, и величина максимальных межламельных напряжений в этом случае зависят от формы и величины воздушного зазора. Поэтому коэффициент магнитной устойчивости в некомпенсированных двигателях определяется специальным расчетом с учетом индивидуальных особенностей проектируемой машины.
Коэффициент максимального искажения магнитного поля
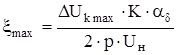 , (4.41)
, (4.41)
где 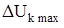 – максимальный уровень межламельного напряжения.
– максимальный уровень межламельного напряжения.
Принимаю 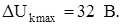
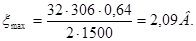
Коэффициент раскрытия воздушного зазора принимаю, 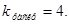
Тогда согласно [1], рисунок 8.3 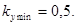
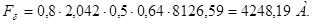
Согласно закону полного тока, сумма падений магнитных напряжений в контуре должна компенсироваться МДС намагничивания
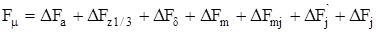 , (4.42)
, (4.42)
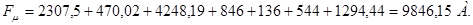
Реальное значение МДС возбуждения главных полюсов
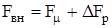 , (4.43)
, (4.43)
где 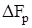 – поперечная составляющая реакции якоря.
– поперечная составляющая реакции якоря.
Наиболее простым методом нахождения составляющей 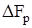 является ее расчет через коэффициент реакции якоря
является ее расчет через коэффициент реакции якоря
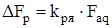 , (4.44)
, (4.44)
В двигателях без компенсационной коэффициент реакции якоря, 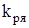 определяется по диаграмме рисунка 8.4.
определяется по диаграмме рисунка 8.4.
Для индукции 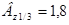 Тл, принимаем
Тл, принимаем 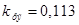 .
.
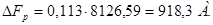
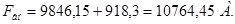
При этом удостоверяемся в правильности выбора 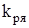 по формуле
по формуле
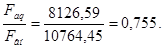
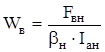 , (4.45)
, (4.45)
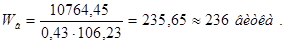
Так как число витков округлили, то необходимо уточнить потребную МДС воздушного зазора. Для этого уточним реальное значение МДС возбуждения главных полюсов.
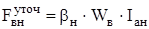 , (4.46)
, (4.46)
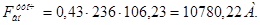
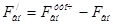 , (4.47)
, (4.47)
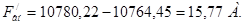
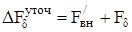 , (4.48)
, (4.48)
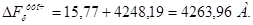
Для определения точных геометрических размеров воздушного зазора сначала рассчитаем эквивалентный воздушный зазор
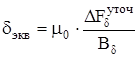 , (4.49)
, (4.49)
где 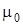 – магнитная постоянная.
– магнитная постоянная. 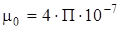 Гн/м.
Гн/м.
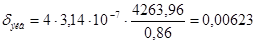 м.
м.
Связь между конструкционными и эквивалентными воздушными зазорами устанавливается через коэффициент Картера по поверхности якоря, учитывающий геометрические размеры зубцового слоя якоря
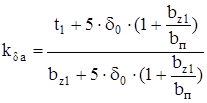 . (4.50)
. (4.50)
Принимаю 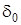 = 3,183 мм.
= 3,183 мм.
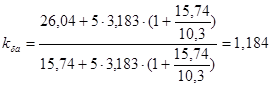 .
.
Найдем коэффициент Картера по поверхности полюса для эксцентричного зазора
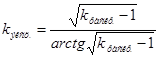 , (4.51)
, (4.51)
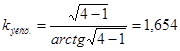 .
.
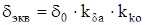 , (4.52)
, (4.52)
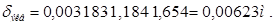
Расчет добавочных полюсов
Из условия равенства реактивной и коммутирующей ЭДС рассчитаем требуемую индукцию в зоне коммутации
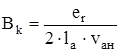 , (6.1)
, (6.1)
где 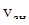 – окружная скорость на поверхности якоря в номинальном режиме.
– окружная скорость на поверхности якоря в номинальном режиме.
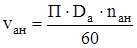 . (6.2)
. (6.2)
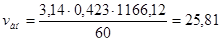 м/с.
м/с.
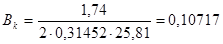 Тл.
Тл.
Для обеспечения требуемого уровня магнитной индукции в зоне коммутации необходимо создать коммутирующий поток
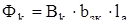 , (6.3)
, (6.3)
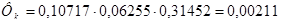 Вб.
Вб.
Полный поток добавочных полюсов
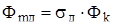 , (6.4)
, (6.4)
где 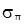 – коэффициент рассеяния добавочного полюса;
– коэффициент рассеяния добавочного полюса;
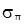 = 3 – в машинах без компенсационной обмотки.
= 3 – в машинах без компенсационной обмотки.
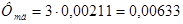 Вб.
Вб.
Чтобы обеспечить линейность магнитной характеристики добавочных полюсов во всем рабочем диапазоне тока якоря, включая и режим максимальной мощности, индукция в сердечнике полюса в номинальном режиме не должна превышать
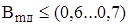 Тл. (6.5)
Тл. (6.5)
Принимаю 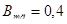 .
.
Наметим ширину сердечника добавочного полюса
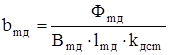 , (6.6)
, (6.6)
где 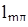 – длина сердечника полюса.
– длина сердечника полюса. 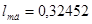 м;
м;
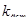 – коэффициент заполнения сердечника сталью.
– коэффициент заполнения сердечника сталью.
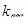 = 1.
= 1.
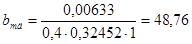 мм.
мм.
Зададимся значением второго воздушного зазора
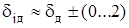 мм, (6.7)
мм, (6.7)
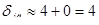 мм.
мм.
Магнитное напряжение первого воздушного зазора
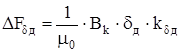 , (6.8)
, (6.8)
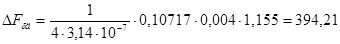 А.
А.
Магнитное напряжение второго воздушного зазора
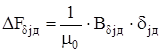 , (6.9)
, (6.9)
Найдем значение индукции в сердечнике добавочного полюса
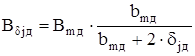 , (6.10)
, (6.10)
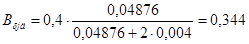 Тл.
Тл.
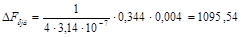 А.
А.
Полная МДС обмотки возбуждения добавочных полюсов
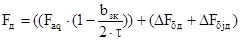 , (6.11)
, (6.11)
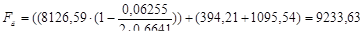 А.
А.
Число витков катушки добавочного полюса
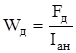 , (6.12)
, (6.12)
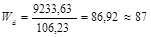 витка.
витка.
Так как число витков округляли, то необходимо уточнить значение МДС обмотки возбуждения добавочных полюсов
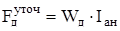 , (6.13)
, (6.13)
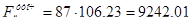 А.
А.
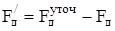 , (6.14)
, (6.14)
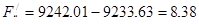 А.
А.
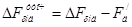 , (6.15)
, (6.15)
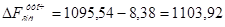 А.
А.
Скорректируем размеры второго воздушного зазора
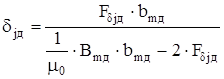 , (6.16)
, (6.16)
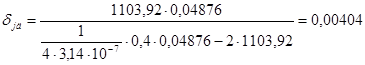 м.
м.
Оценим площадь поперечного сечения проводников обмотки
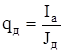 , (6.17)
, (6.17)
где J 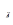 - максимально допустимая плотность тока в проводниках обмотки, принимаю J
- максимально допустимая плотность тока в проводниках обмотки, принимаю J 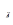 = 3,5 А/мм
= 3,5 А/мм 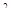
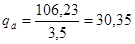 мм2.
мм2.
Укладку производим на широкое ребро в семь слоев по высоте тела добавочного полюса.
По значению q 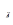 намечаем размеры проводника обмотки возбуждения добавочных полюсов
намечаем размеры проводника обмотки возбуждения добавочных полюсов
hпр × bпр = 22 × 1,81, qд = 39,1 мм2, (6.18)
Найдем размер катушки по высоте в нашем случае
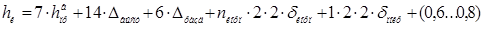 , (6.19)
, (6.19)
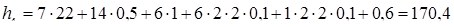 мм.
мм.
Тогда размеры четырех крайних к остову слоев катушки по ширине, при условии, что в них по 12 витков
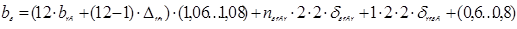 , (6.20)
, (6.20)
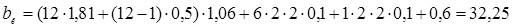 мм.
мм.
Средняя длина витка добавочного полюса
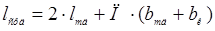 , (6.21)
, (6.21)
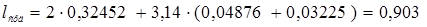 м.
м.
Сопротивление цепей обмоток добавочных полюсов 20°С
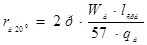 , (6.22)
, (6.22)
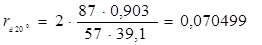 Ом.
Ом.
Масса меди катушек добавочных полюсов
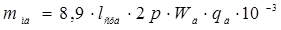 , (6.23)
, (6.23)
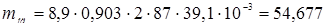 кг.
кг.
Содержание
Введение3
Исходные данные4
1. Расчет параметров зубчатой передачи и основных размеров5
2. Расчет активного слоя якоря
2.1 Расчет параметров обмотки
2.2 Параметры обмотки якоря
3. Расчет щеточно-коллекторного узла
3.1 Выбор числа и размера щеток
3.2 Определение рабочей длины коллектора
4. Расчет магнитной цепи
4.1 Сердечник якоря
4.2 Главные полюса
4.3 Остов
4.4 Участок сердечника якоря
4.5 Участок зубцового слоя якоря
4.6 Участок сердечника главного полюса
4.7 Участок стыка полюса с остовом
4.8 Участок выхода потока из полюса в остов
4.9 Ярмо остова
4.10 Расчет воздушного зазора
4.11 Расчет конструкционных размеров и параметров катушки
главного полюса
5. Расчет стационарной коммутации
6. Расчет добавочных полюсов
Список использованных источников
Введение
В настоящее время совершенствование электроподвижного состава является одним из главных направлений в развитии железнодорожного транспорта и остается таковым в ближайшей перспективе. Развитие средств электроники и микропроцессорной техники способствует появлению принципиально новых по своим техническим возможностям локомотивов с высоким уровнем автоматизации процессов управления. Однако каковы бы ни были масштабы внедрения новых средств автоматизированного контроля и управления техническими системами электрических локомотивов, их реализуемые эксплуатационные качества всегда будут определяться техническими возможностями их движителей – тяговых электродвигателей (ТЭД).
В этих условиях исключительно важная роль отводится процессу проектирования тяговых электродвигателей. В ходе разработки новой конструкции приходиться неоднократно уточнять и тщательно увязывать мужду собой множество размеров и параметров машины для одновременного учета и выполнения многочисленных конструкторских, технологических, экономических требований и ограничений.
В данном курсовом проекте основное внимание уделено вопросам разработки конструкции основных частей машины и их взаимосвязи в единой системе тягового двигателя. Необходимо отметить, что в своей основе методика проектирования тягового электрического двигателя, опирается на традиционную методику проектирования тяговых машин, разработанную и используемую в настоящее время коллективами проектировщиков отечественного электровозостроения.
Исходные данные
Номинальная мощность двигателя P 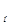 = 145 кВт;
= 145 кВт;
Номинальное напряжение питания двигателя U 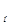 = 1500 В;
= 1500 В;
Корпусное напряжение U 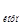 = 3000 В;
= 3000 В;
Номинальная скорость движения локомотива V 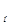 = 48 км/ч;
= 48 км/ч;
Конструкционная скорость движения локомотива V 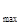 = 98 км/ч;
= 98 км/ч;
Номинальный коэффициент регулирования возбуждения β 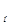 = 0,43;
= 0,43;
Диаметр бандажей ведущих колес D 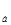 = 1,05 м;
= 1,05 м;
Диаметр оси колесной пары d 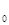 = 180 мм;
= 180 мм;
Вид торможения рекуперативное;
Вид системы вентиляции машины самовентиляция;
Род тока постоянный;
Вид локомотива МВПС;
Тип подвешивания двигателя опорно - рамное;
Класс изоляции “B”.
Расчет параметров зубчатой передачи и основных размеров
Предварительно из ряда параметров, обеспечивающих минимум отходов при раскройке места, выбираем размер диаметра якоря
Dа = 423 мм. (1.1)
Выполняя требование Dк = (0,75…0,9) · Dа, рассчитывается диаметр коллектора
Dк @ 0,9 · Dа , (1.2)
Dк @ 0,9 · 423 = 380,7 мм.
Минимальное число коллекторных пластин рассчитывается по формуле
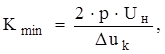 (1.3)
(1.3)
где 2р – число коллекторных полюсов. Принимаю 2р = 2;
Duк – среднее максимальное напряжение. Принимаю Duк = 18 В.
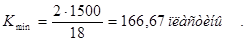
Максимальное число коллекторных пластин рассчитывается по формуле
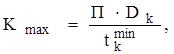 (1.4)
(1.4)
где tкmin – минимальный шаг по коллектору. Принимаю tкmin = 3,9 мм.
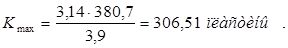
Принимаю К = 306 пластин.
Уточняем диаметр коллектора
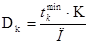 , (1.5)
, (1.5)
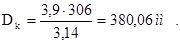
Уточняем межламельное напряжение
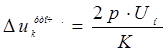 , (1.6)
, (1.6)
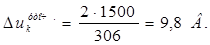
Для двигателей МВС, допустимая максимальная частота вращения якоря обычно не выходит за пределы 3000 об/мин.
Тогда максимальные обороты якоря
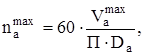 (1.7)
(1.7)
где 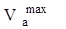 – максимальная окружная скорость якоря.
– максимальная окружная скорость якоря. 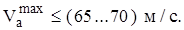
Принимаю 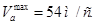
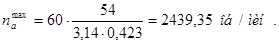
Зная максимально возможные обороты якоря,можно найти максимально возможное передаточное число редуктора µ
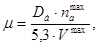 (1.8)
(1.8)
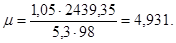
Номинальная частота вращения двигателя рассчитывается как
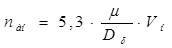 , (1.9)
, (1.9)
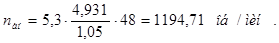
Диаметр делительной окружности зубчатого колеса находится по формуле
Dz = Dб – 2 · (b+D), (1.10)
где b – расстояние от головки рельса до кожуха редуктора. b = 120 мм;
D – расстояние от делительной окружности большого зубчатого колеса
до внешней нижней точки кожуха редуктора. D = 20 мм.
Dz = 1050 – 2 · (120+20) = 770 мм.
Далее находится диаметр делительной окружности малого зубчатого колеса
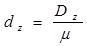 , (1.11)
, (1.11)
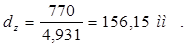
Число зубьев большого зубчатого колеса
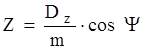 , (1.12)
, (1.12)
где y – угол наклона зубьев при прямозубой передаче. Принимаю y = 0о;
m – модуль зубчатого зацепления, принимаемый в зависимости от
вращающего момента М и конструкции тяговой передачи.
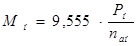 , (1.13)
, (1.13)
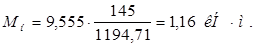
По эмпирическим формулам для прямозубых передач
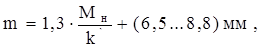 (1.14)
(1.14)
где К – односторонняя передача. Принимаю К = 1, согласно [1].
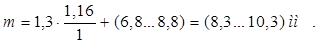
Принимаем m = 10.
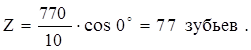
Число зубьев шестерни рассчитывается по формуле
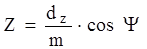 , (1.15)
, (1.15)
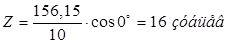
Тогда точное значение передаточного числа редуктора
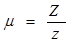 , (1.16)
, (1.16)
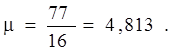
Диаметр конца вала рассчитывается по формуле
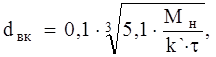 (1.17)
(1.17)
где 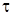 – при односторонней передаче. Принимаю
– при односторонней передаче. Принимаю 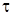 = 10 МПа.
= 10 МПа.
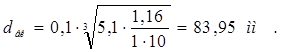
Проверка по ширине шестерни. bш 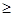 (20…25) мм
(20…25) мм
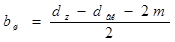 , (1.18)
, (1.18)
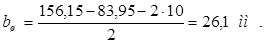
Уточняем значения максимальной и номинальной частот вращения
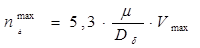 , (1.19)
, (1.19)
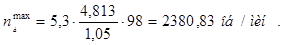
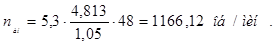
Уточняем значения максимальных окружных скоростей якоря и коллектора
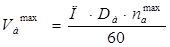 , (1.20)
, (1.20)
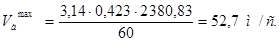
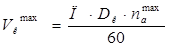 , (1.21)
, (1.21)
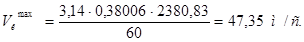
Определяем величину централи двигателя
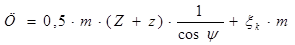 , (1.22)
, (1.22)
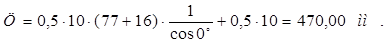
Величина централи характеризует то пространство, которое отводиться для вписывания габаритов проектируемого двигателя. Но поскольку конструкционные размеры двигателя пока неизвестны, можно только ориентировочно проверить возможность такого вписывания по соотношению централи и диаметра якоря - как основного параметра машины, задающего его внешние габариты.
При 2р = 2 и опорно-рамном подвешивании
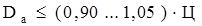 , (1.23)
, (1.23)
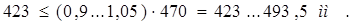
Расчет активного слоя якоря
Расчет параметров обмотки
Общее число проводников обмотки якоря
N = 2 · K, (2.1)
N = 2 · 306 = 612 проводников.
Ток якоря в номинальном режиме
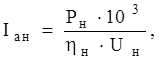 (2.2)
(2.2)
где hн – КПД двигателя. Принимаю hн = 0,91, согласно [1].
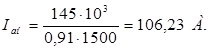
Выбираем простую петлевую обмотку якоря, у которой 2а = 2р.
Линейная токовая нагрузка якоря
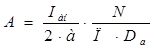 , (2.3)
, (2.3)
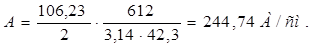
Ток параллельной ветви
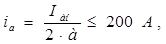 (2.4)
(2.4)
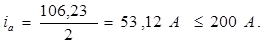
При определении рационального числа пазов Z учитывается ограничение по условиям нагрева пучка проводников в пазу якоря в виде величины объема тока в пазу
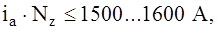 (2.5)
(2.5)
где Nz – число проводников в одном пазу. Принимаю Nz = 2 uk = 12.
53,12 · 12 = 637,44 А 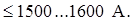
Неравенство (2.5) выполняется.
Число пазов якоря находится по формуле
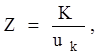 (2.6)
(2.6)
где uk – число коллекторных пластин на паз. Принимаю uk = 6.
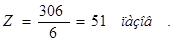
Первый шаг обмотки в реальных пазах должен удовлетворять условию
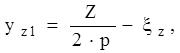 (2.7)
(2.7)
где 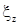 – укорочение шага обмотки якоря в реальных пазах.
– укорочение шага обмотки якоря в реальных пазах.
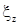 = 0,5 паза при петлевой обмотке.
= 0,5 паза при петлевой обмотке.
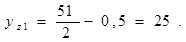
Произведем окончательную увязку между собой числа пазов Z, проводников N и коллекторных пластин К, которая должна обеспечивать выполнение требования внутренней симметрии обмотки якоря
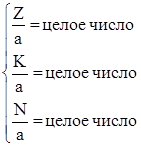 , (2.8)
, (2.8)
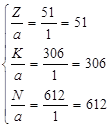 .
.
Найдем допустимое значение плотности тока в проводниках якоря
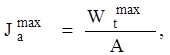 (2.9)
(2.9)
где Wtmax – допустимый предел теплового фактора машины.
Принимаю Wtmax = 2050 согласно [1].
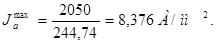
Расчетная величина Ja не должна превышать (5…6) А/мм2.
Принимаю Ja = 6 А/мм2.
Наметим площадь поперечного сечения активного проводника якоря
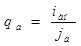 , (2.10)
, (2.10)
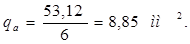
По значению qа намечаем размеры проводника hпр × bпр.
По ГОСТ 434-53, приложение А согласно [1], выбираю проводник с размерами
hпр × bпр = 1,4 × 6,7 qпр = 9,165 мм2. (2.11)
Уточним допустимое значение плотности тока в проводниках якоря
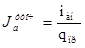 , (2.12)
, (2.12)
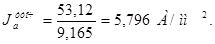
Проведем проверку правильности выбора сечения проводника
A · ja < 2050 A, (2.13)
244,74 · 5,796 = 1418,51 А < 2050 A.
Неравенство (2.13) выполняется.
Высоту паза якоря находим по выражению
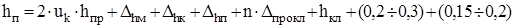 , (2.14)
, (2.14)
где Dпрокл – толщина изоляционных прокладок Dпрокл = 0,5 мм;
nпрокл – число прокладок. nпрокл = 3;
hкл – высота клина. hкл = 4 мм;
nкорп – число слоев корпусной изоляции. nкорп =6;
Dhм – толщина межвитковой изоляции по высоте паза якоря;
Dhк – толщина корпусной изоляции по высоте паза якоря;
Dhп – толщина покровной изоляции по высоте паза якоря;
(0,2…0,3) – зазор на укладку секций в паз;
(0,15…0,2) – разница между размером паза в свету и размером паза в
штампе.
Принимаю: 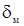 = 0,1 мм,
= 0,1 мм, 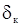 = 0,1 мм,
= 0,1 мм, 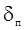 = 0,1мм.
= 0,1мм.
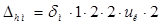 , (2.15)
, (2.15)
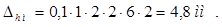
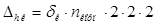 , (2.16)
, (2.16)
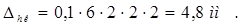
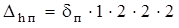 , (2.17)
, (2.17)
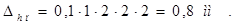
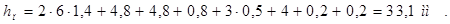
Ширину паза якоря вычисляем по формуле
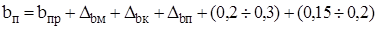 , (2.18)
, (2.18)
где Dbм – толщина межвитковой изоляции по ширине паза якоря;
Dbк – толщина корпусной изоляции по ширине паза якоря;
Dbп – толщина покровной изоляции по ширине паза якоря;
(0,2…0,3) – зазор на укладку секций в паз;
(0,15…0,2) – разница между размером паза в свету и размером паза.
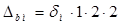 , (2.19)
, (2.19)
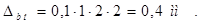
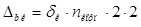 , (2.20)
, (2.20)
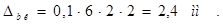
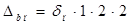 , (2.21)
, (2.21)
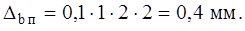
Найдем ширину паза якоря
bп = 6,7 + 0,4 + 2,4 + 0,4 + 0,2 + 0,2 = 10,3 мм.
Полученные размеры паза якоря должны удовлетворять следующим условиям:
– bп = 10,3 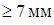 – удовлетворяет;
– удовлетворяет;
– hп = 33,1 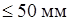 – удовлетворяет.
– удовлетворяет.
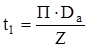 , (2.22)
, (2.22)
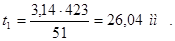
Ширина зубца на поверхности якоря bz1
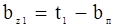 , (2.23)
, (2.23)
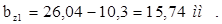
Шаг по пазам в расчетном сечении tz1/3 (на высоте 1/3hп )
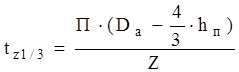 , (2.24)
, (2.24)
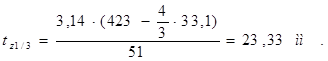
Ширина зубца в расчетном сечении bz1/3
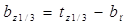 , (2.25)
, (2.25)
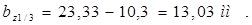
Шаг по дну пазов
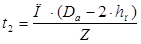 , (2.26)
, (2.26)
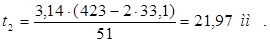
Ширина зубца у основания bz2
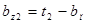 , (2.27)
, (2.27)
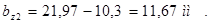
Необходимо проконтролировать, чтобы выполнялось условие
bz2 ³ 7 мм, для обеспечения достаточной механической прочности зубца.
Магнитный поток находим по выражению
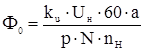 , (2.28)
, (2.28)
где ku – коэффициент, учитывающий потери напряжения на внутренних
сопротивлениях обмоток двигателя.
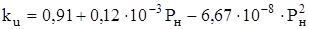 , (2.29)
, (2.29)
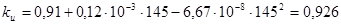 .
.
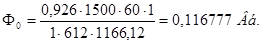
Далее определяем длину шихтованного пакета якоря
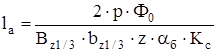 , (2.30)
, (2.30)
где Вz1/3 – индукция в зубцах якоря. Принимаю Вz1/3 = 1,8 Тл;
ad – расчетный коэффициент полюсного перекрытия, для машины без
компенсационной обмоткой. Принимаю ad = 0,64;
Кс – коэффициент заполнения пакета сталью. Принимаю Кс = 0,97.
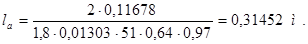
la 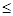 315 мм при опорно-рамном подвешивании и односторонней зубчатой передаче, что удовлетворяет условию.
315 мм при опорно-рамном подвешивании и односторонней зубчатой передаче, что удовлетворяет условию.
Параметры обмотки якоря
Выбрав тип обмотки и геометрию активного слоя якоря, устанавливаю шаги обмотки якоря.
Результирующий шаг обмотки в элементарных пазах или шаг по коллектору в коллекторных делениях при простой петлевой обмотке
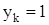 . (2.31)
. (2.31)
Первый шаг в коллекторных делениях
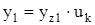 , (2.32)
, (2.32)
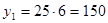 .
.
Второй шаг в коллекторных делениях для простой петлевой обмотки
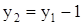 , (2.33)
, (2.33)
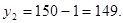 .
.
Укорочение обмотки в коллекторных делениях
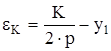 , (2.34)
, (2.34)
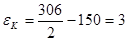 .
.
Полюсное деление по окружности якоря
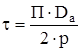 , (2.35)
, (2.35)
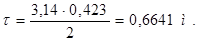
Длина передних и задних лобовых участков якорных проводников
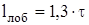 , (2.36)
, (2.36)
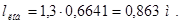 .
.
Длина полувитка обмотки якоря
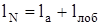 , (2.37)
, (2.37)
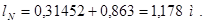
Общая длина проводников обмотки якоря
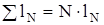 . (2.38)
. (2.38)
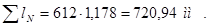
Сопротивление обмотки якоря при 20˚С
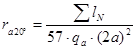 , (2.39)
, (2.39)
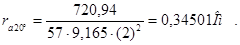
Масса меди обмотки якоря
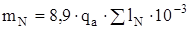 , (2.40)
, (2.40)
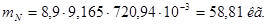
Дата: 2019-07-31, просмотров: 277.