Ответ: Расчеты токов трехфазных КЗ в трехфазных симметричных сетях производятся на одну фазу вследствие подобия явлений, происходящих в каждой из фаз, и равенства значений по фазам одноименных величин. При несимметрии в произвольной точке системы сопротивления в фазах неодинаковы и по этим причинам явления по фазам различны. Неодинаковы в этом случае токи, напряжения и углы сдвига между ними в различных фазах. Для определения токов и напряжений в любой фазе несимметричной системы необходимо составить схему замещения и написать необходимое число уравнений с учетом взаимоиндукции, что усложняет решение задач. Сравнительно просто расчеты несимметричных режимов в трехфазных сетях осуществляются с помощью метода симметричных составляющих. Вычисление токов и напряжений в этом случае сводится к определению этих величин при некотором фиктивном трехфазном КЗ, что дает возможность вновь воспользоваться однолинейной схемой замещения и произвести расчет на одну фазу. В этом заключается одно из основных достоинств метода симметричных составляющих. Произвольную несимметричную систему трех векторов (напряжения, токи, потоки): 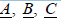 можно разложить однозначно на три симметричные системы: - систему векторов прямой последовательности
можно разложить однозначно на три симметричные системы: - систему векторов прямой последовательности 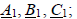 - систему векторов обратной последовательности
- систему векторов обратной последовательности 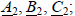 - систему векторов нулевой последовательности
- систему векторов нулевой последовательности 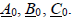
Согласно условию разложения имеем: 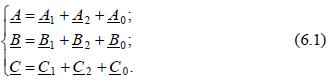 Для сведения уравнений (6.1) к трем неизвестным вводят оператор фазы a. Модуль оператора фазы а равен 1. Таким образом, если любой вектор умножить на a, то модуль вектора не изменится, а лишь произойдет его поворот на 120º против часовой стрелки. Оператор фазы а определяется из соотношений:
Для сведения уравнений (6.1) к трем неизвестным вводят оператор фазы a. Модуль оператора фазы а равен 1. Таким образом, если любой вектор умножить на a, то модуль вектора не изменится, а лишь произойдет его поворот на 120º против часовой стрелки. Оператор фазы а определяется из соотношений: 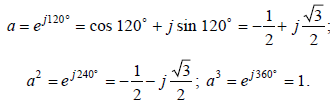 Благодаря этому свойству векторы каждой из симметричных систем (прямой, обратной, нулевой) можно выразить через один вектор той же системы, т. е. три неизвестных в каждом уравнении свести к одному. Если принять в качестве основной фазу А, то систему векторов (6.1) при помощи оператора фазы а можно представить в следующем виде:
Благодаря этому свойству векторы каждой из симметричных систем (прямой, обратной, нулевой) можно выразить через один вектор той же системы, т. е. три неизвестных в каждом уравнении свести к одному. Если принять в качестве основной фазу А, то систему векторов (6.1) при помощи оператора фазы а можно представить в следующем виде:
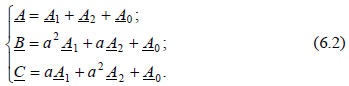 Совместное решение системы уравнений (6.2) дает
Совместное решение системы уравнений (6.2) дает 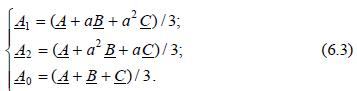 В соответствии с уравнениями (6.3) по известным несимметричным векторам
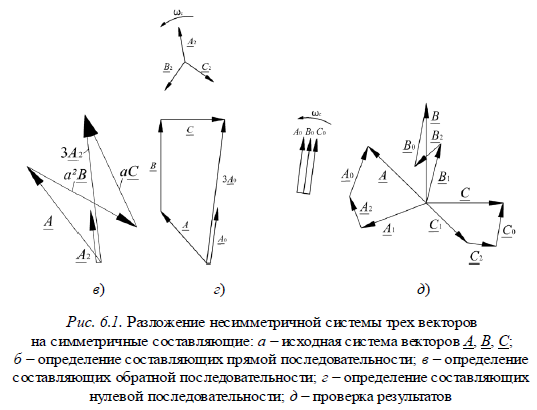
В соответствии с уравнениями (6.3) по известным несимметричным векторам 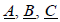 можно найти их симметричные составляющие графическим или аналитическим способами. Пример графическогоопределения симметричных составляющих несимметричной трехфазной системы приведен на рис. 6.1.
можно найти их симметричные составляющие графическим или аналитическим способами. Пример графическогоопределения симметричных составляющих несимметричной трехфазной системы приведен на рис. 6.1.
Степень несимметрии трехфазной системы оценивается коэффициентами несимметрии и неуравновешенности системы. Коэффициентом несимметрии системы b называется абсолютная
величина отношения составляющей напряжения обратной последова-
тельности к прямой  Коэффициентом неуравновешенности системы К называется абсолютная величина отношения составляющей напряжения нулевой последовательности к прямой
Коэффициентом неуравновешенности системы К называется абсолютная величина отношения составляющей напряжения нулевой последовательности к прямой  Системы прямой и обратной последовательности являются симметричными и уравновешенными, а система нулевой последовательности является симметричной, но неуравновешенной. Система нулевой последовательности может существовать только в неуравновешенных системах, которые характеризуются следующим условием:
Системы прямой и обратной последовательности являются симметричными и уравновешенными, а система нулевой последовательности является симметричной, но неуравновешенной. Система нулевой последовательности может существовать только в неуравновешенных системах, которые характеризуются следующим условием: 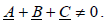 Геометрическая сумма неуравновешенной системы фазных токов равна утроенному току нулевой последовательности, который протекает в земле или нулевом проводе.
Геометрическая сумма неуравновешенной системы фазных токов равна утроенному току нулевой последовательности, который протекает в земле или нулевом проводе.
Дата: 2019-07-30, просмотров: 335.