Ответ: Основные уравнения падений напряжений в схемах каждой последовательности, составленные для симметричной части системы, при чисто индуктивной цепи можно представить в виде:

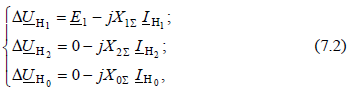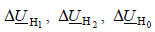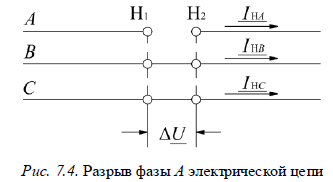
 где – симметричные составляющие падения напряжения фазы А на несимметричном участке системы; результирующие реактивности схем отдельных последовательностей относительно места продольной несимметрии. На рис. 7.4 изображен несимметричный участок системы, в которой возникла продольная несимметрия при разрыве фазы А. Полагая, что разрыв фазы А происходит на малом отрезке, можно считать, что падения напряжений фаз В и С на длине этого участка равны нулю. В этом случае по месту несимметрии имеем следующие граничные условия:

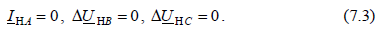
 При разложении падений напряжений на симметричные составляющие с учетом граничных условий (7.3) получим:

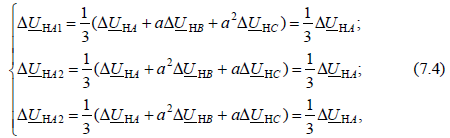 т. е.

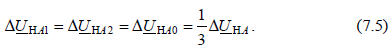 Напряжение между точками Н1 и Н2 поврежденной фазы А из (7.5) будет Из основных уравнений (7.2) с учетом (7.5) для симметричных составляющих 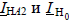имеем: 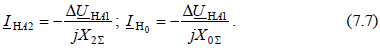Расписав условие через симметричные составляющие тока и подставив вместо 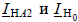их значения из (7.7), получим: 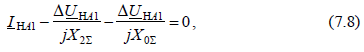откуда найдем  где Теперь из (7.2) и (7.9) определим 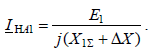Из выражений (7.7) с учетом (7.10) для токов обратной и нулевой последовательностей имеем:

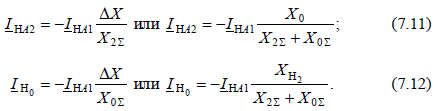 Для определения напряжений с одной из сторон продольной несимметрии следует предварительно найти по схемам отдельных последовательностей симметричной части сети соответствующие составляющие этих напряжений. Прибавив к последним соответствующие напряжения 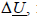находим симметричные составляющие напряжений с

другой стороны продольной несимметрии. Зная все симметричные составляющие токов и напряжений, можно определить фазные величины токов и напряжений. В частности, для определения фазных токов в месте разрыва одной фазы могут быть использованы выражения: 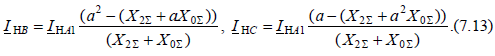Для нахождения модуля фазных токов при разрыве одной фазы может быть использован коэффициент, определяемый по выражению 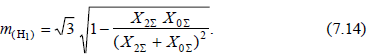Модуль фазных токов неповрежденных фаз определится 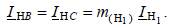Соотношение (7.10) позволяет составить комплексную схему замещения (рис. 7.5) для случая разрыва одной из фаз.

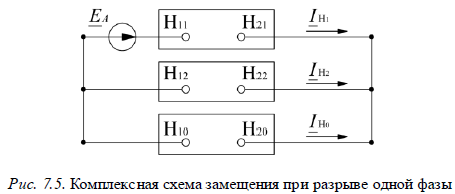 На рис. 7.6, а приведена схема, для которой составлена комплексная схема замещения (рис. 7.6, б) при разрыве одной из фаз в начале линии. Складывая последовательно реактивности в схеме замещения обратной последовательности, получим 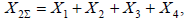и, соответственно, в схеме замещения нулевой последовательности: 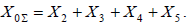Комплексная схема замещения приводится к более простому

виду (рис. 7.6, в). Результирующая ЭДС схемы прямой последовательности в данном случае численно равна Е1, а суммарное реактивное сопротивление

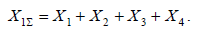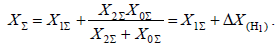
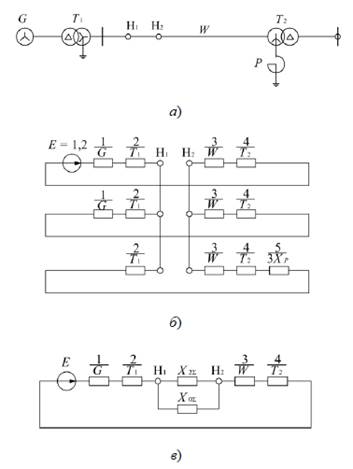
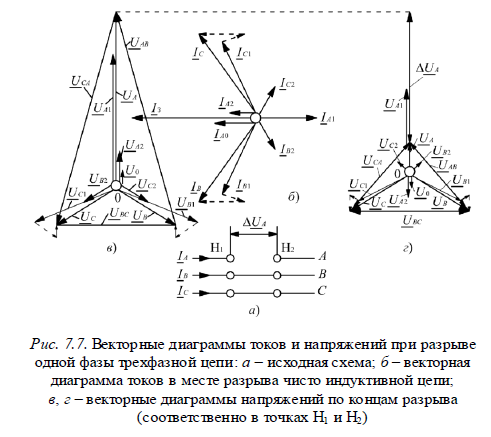
Суммарное сопротивление для определения токов прямой последовательности 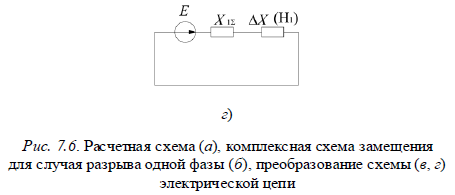Схема любой сложности при продольной несимметрии сводится к виду, изображенному на рис. 7.6, г. Следует всегда помнить, что в этой схеме результирующая ЭДС находится из схемы замещения только прямой последовательности относительно места несимметрии. Векторные диаграммы токов и напряжений. Зная все симметричные составляющие токов и напряжений, определяют фазные величины токов и напряжений. В частности, для определения фазных токов в месте разрыва одной фазы могут быть использованы выражения (7.13). Для нахождения модуля фазных токов при разрыве одной фазы может быть использован коэффициент, определяемый по выражению (7.14). На рис. 7.7 приведены векторные диаграммы токов и напряжений в месте разрыва фазы А.