Процедура выравнивания, сглаживания анализируемого распределения заключается в замене эмпирических частот теоретическими, определяемыми по формуле теоретического распределения, но с учетом фактических значений переменной. На основе сопоставления эмпирических и теоретических частот рассчитываются критерии согласия, которые используются для проверки гипотезы о соответствии исследуемого распределения тому или иному типу теоретических распределении.

Выбор конкретного типа модельного распределения осуществляется исходя из самых общих соображений, опирающихся на визуальный анализ построенных графиков распределения. В практическом анализе обязательной является проверка соответствия изучаемого распределения нормальному закону распределения. Необходимость этого связана с тем, что условием применения значительного числа статистических характеристик и оценок является наличие нормального распределения.

Проверка гипотезы о нормальном распределении регионов России по числу автомобилей на душу населения в 1990 году основывается на расчёте критерия

,

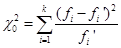где 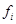 – эмпирические абсолютные частоты,  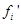– абсолютные частоты теоретического распределения, k – число интервалов.

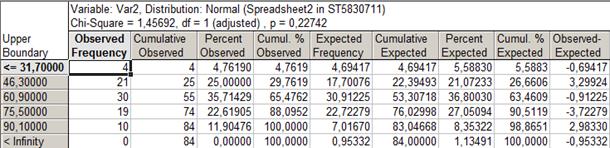
Таблица 6.1. Проверка гипотезы о нормальном распределении регионов России по числу автомобилей на душу населения в 1990 году

Формулы, по которым рассчитывается плотность модельного распределения, а также формулы для расчета теоретических частот распределения могут быть легко найдены в общедоступной справочной и учебной литературе. В данной лабораторной работе используются формулы для нормального распределения.

Функция нормального распределения: 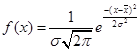, плотность нормального распределения:

,

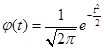где 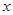 – значение изучаемого признака, 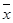- средняя арифметическая величина, 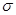- среднее квадратическое отклонение изучаемого признака, e, π – математические константы,  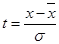– нормированное отклонение.

Теоретические частоты нормального отклонения рассчитываются по следующей формуле:

,

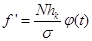где N – объём совокупности, h_k – величина интервала. В моём случае вариационный ряд построен с использованием равных интервалов, следовательно: .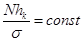

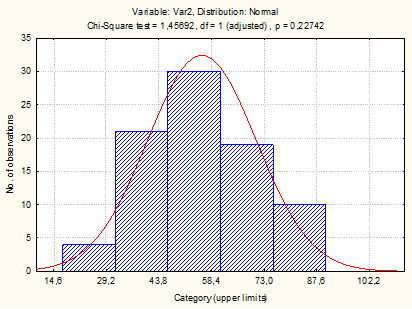
Рис. 6.1. Гистограмма и расчётная кривая распределения регионов России по числу собственных легковых автомобилей на 1000 человек населения в 1990 г.

В шапке таблицы находятся следующие показатели: 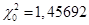, 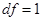(уточнённое значение числа степеней свободы,

,

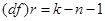где k – число интервалов вариационного ряда, n – число параметров теоретического распределения, определяемых по опытным данным, для нормального закона n=2, p – расчётный уровень значимости).

Принятие решения о справедливости гипотезы о законе распределения можно осуществить, ориентируясь на эмпирическое значение критерия 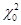, который сравнивается с табличным значением 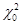. Окончательные выводы по проверке гипотезы о законе распределения: так как 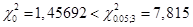, то гипотеза о нормальном распределении регионов России по числу собственных легковых автомобилей на 1000 человек населения в 1990 г. не противоречит истине.

Заключение

Только в тридцати регионах России, что составляет 35,71% от общего числа регионов, количество автомобилей на 1000 человек населения в 1990 году составляло от 46,3 до 60,9 штук. В пятидесяти пяти регионах России (65,47% от всех регионов) количество автомобилей на 1000 человек населения в 1990 году составляло менее 60,9 штук.

В среднем в регионах России количество автомобилей на 1000 человек населения в 1990 году составляло 55,71 штуку. В 50% регионов России количество автомобилей на 1000 человек населения в 1990 году было меньше 56,15 штук, а в другой половине – больше.

Размах вариации, разность между максимальным и минимальным значениями совокупности, составляет 73 единицы. В 1990 году в регионах России число автомобилей на 1000 человек населения отличалось от среднего по стране на 15,0952 штук. Коэффициент вариации оценивает степень количественной однородности изучаемой совокупности. В данном случае совокупность можно признать однородной, т. к. коэффициент вариации меньше 33% (V=27,098%).

В 50% регионов России количество автомобилей на 1000 человек населения в 1990 году составляло от 44,80 до 65,80 штук.

Распределение имеет очень незначительную правостороннюю асимметрию, кроме того есть незначительный отрицательный эксцесс, это значит, что в совокупности не сформировалось «ядро» распределения.

Данное распределение соответствует нормальному закону распределения по критерию Пирсона.