Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Во многих случаях практики интерес представляет вопрос о том, в какой мере существенно влияние того или иного фактора на рассматриваемый признак. В данном случае фактором является вид инфекции вызвавший реактивный артрит, а признаками СОЭ, СРБ, Фибриноген, гемоглобин, ВАШБП и ВАШСП. Научное обоснованное решение подобной задачи при некоторых предположениях составляет предмет дисперсионного анализа.

Статистическая модель

Выборки производятся из нормальных совокупностей. Первая выборка производиться из совокупности со средним 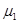, вторая - со средним  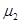, k-я из совокупности со средним 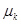. Все наблюдения независимы.

Критическая область.

Если значение p 0, то нулевая гипотеза может быть отвергнута, т.е. хотя бы одно среднее арифметическое отличается от остальных значений. Выберем критический уровень значимости p_KP для условия принятия нулевой гипотезы pкр=0,05

p>pкр

 Гипотезы №1.

 Н₀ : =  =…=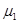

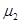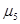
 Н₁: не все средние равны.

Так как данный метод работает только для нормальных совокупностей то сначала построим графики функций распределения для каждой выборки.

Для экономии времени и упрощения расчетов воспользуемся Matlab.

 

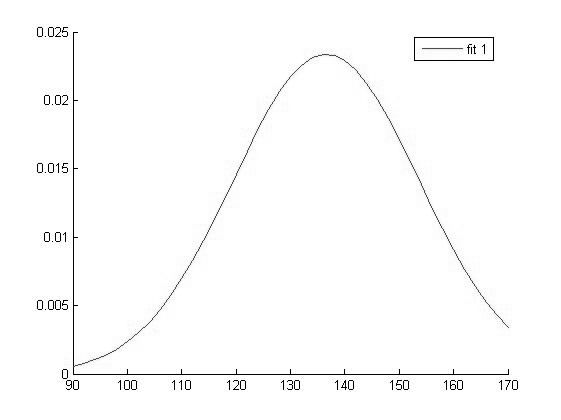График функции распределения для значений Hb в 1 группе

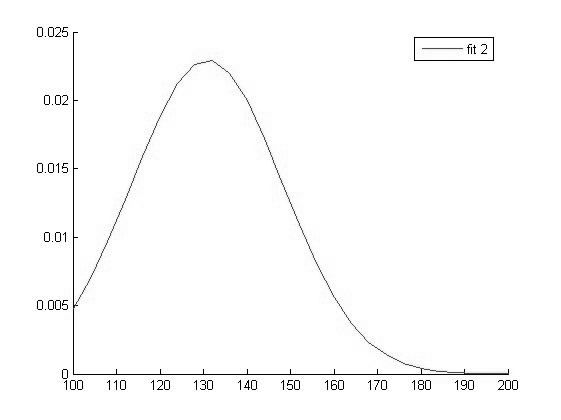График функции распределения для значений Hb в 2 группе

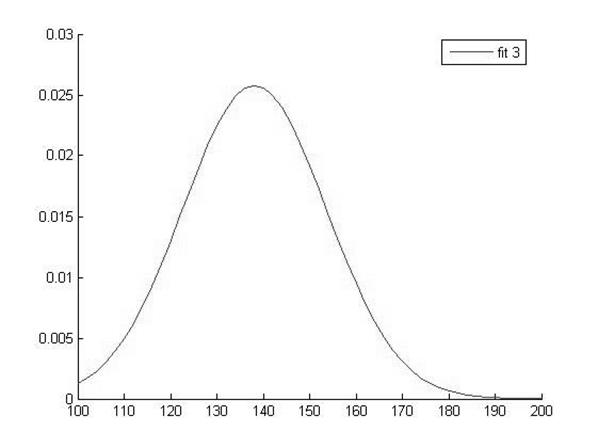График функции распределения для значений Hb в 3 группе

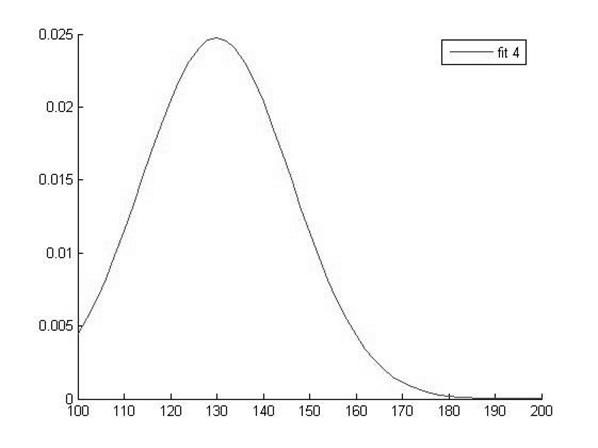График функции распределения для значений Hb в 4 группе

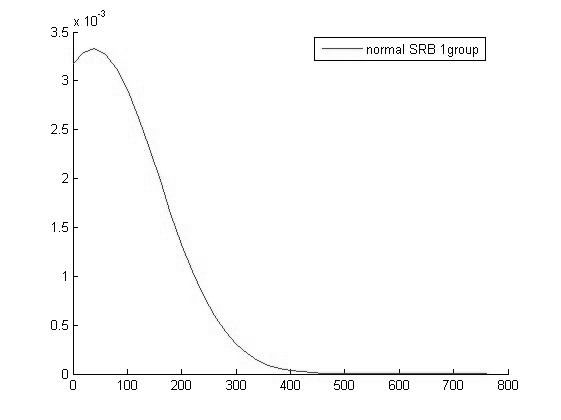График функции распределения для значений СРБ в 1 группе

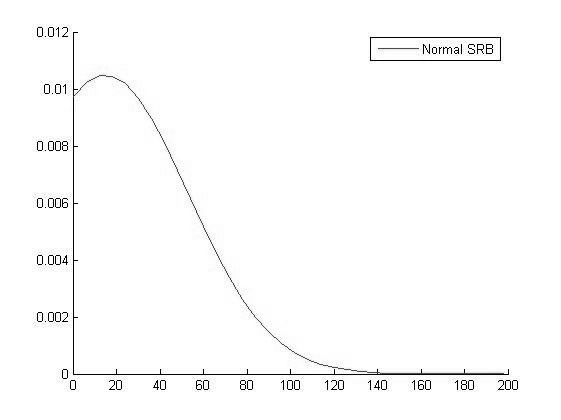График функции распределения для значений СРБ в 2 группе

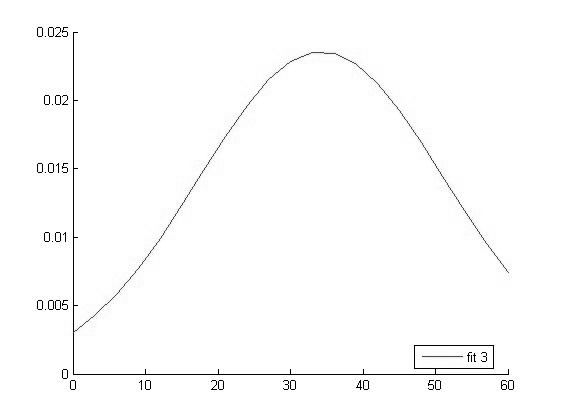График функции распределения для значений СРБ в 3 группе

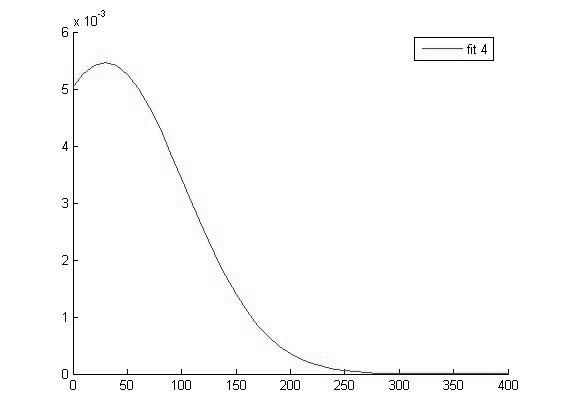График функции распределения для значений СРБ в 4 группе

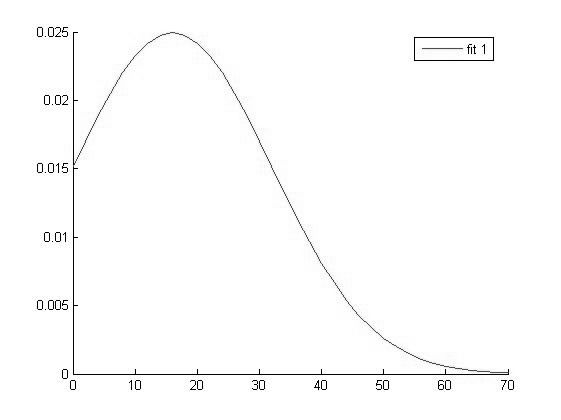График функции распределения для значений СОЭ в 1 группе

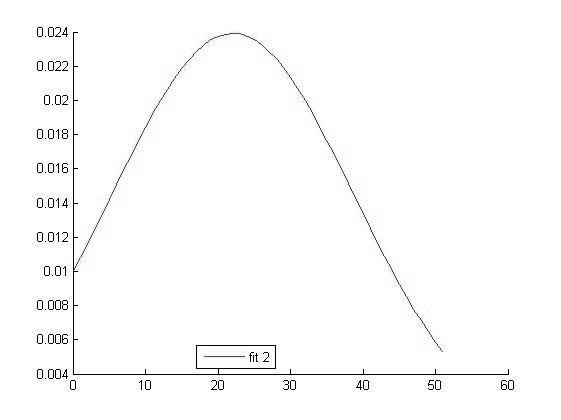График функции распределения для значений СОЭ в 2 группе

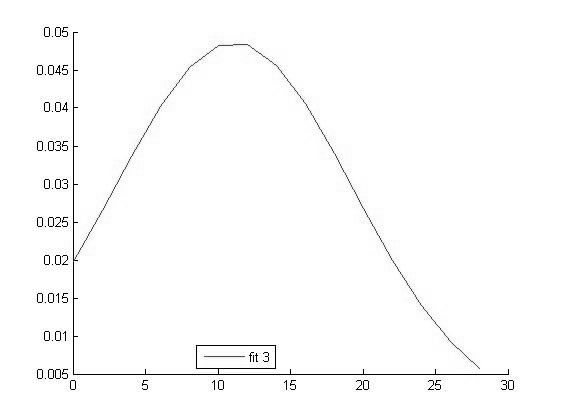График функции распределения для значений СОЭ в 3 группе

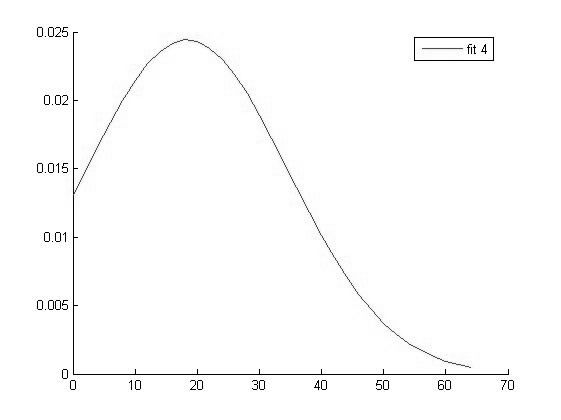График функции распределения для значений СОЭ в 4 группе

График функции распределения для значений Фибриногена в 1 группе

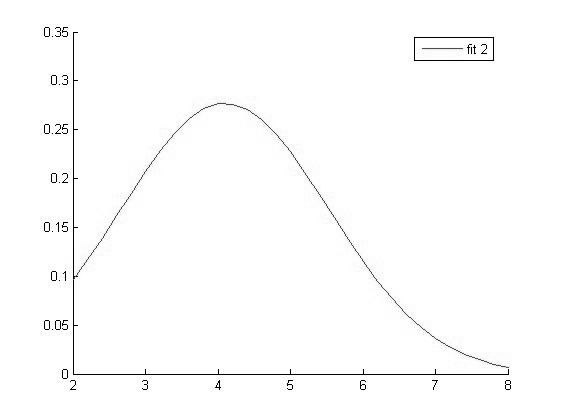График функции распределения для значений Фибриногена в 2 группе

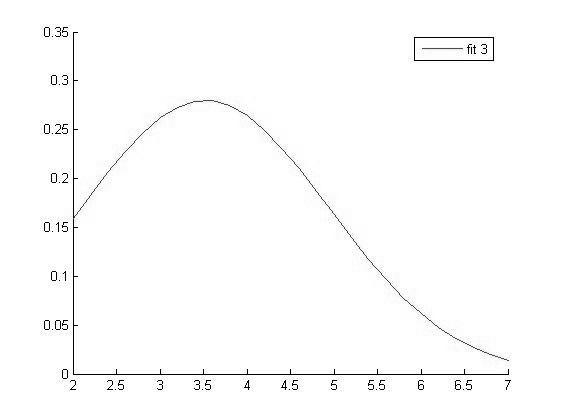График функции распределения для значений Фибриногена в 3 группе

График функции распределения для значений Фибриногена в 4 группе

График функции распределения для значений ВАШБП в 1 группе

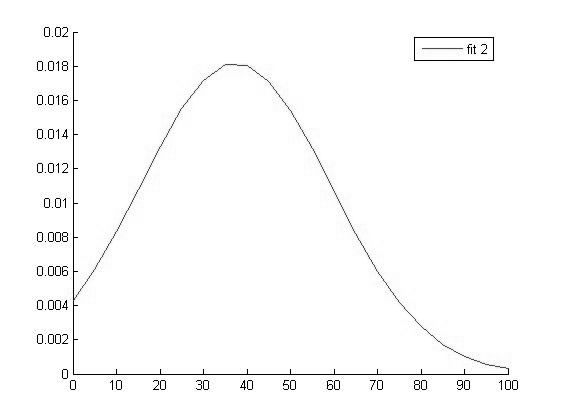График функции распределения для значений ВАШБП в 2 группе

График функции распределения для значений ВАШБП в 3 группе

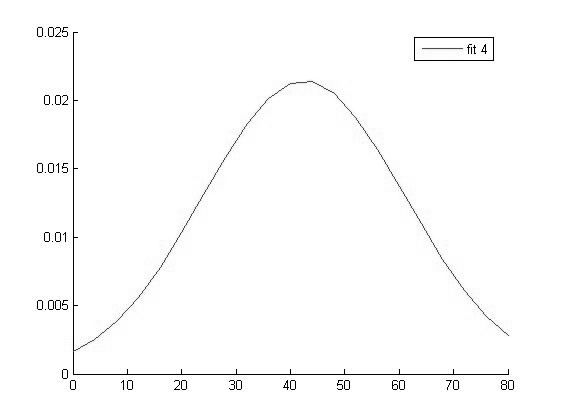График функции распределения для значений ВАШБП в 4 группе

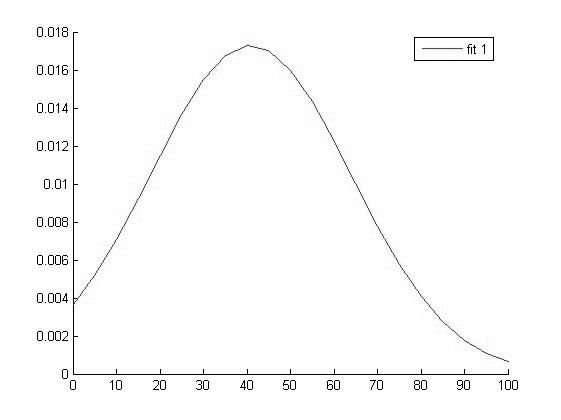График функции распределения для значений ВАШСП в 1 группе

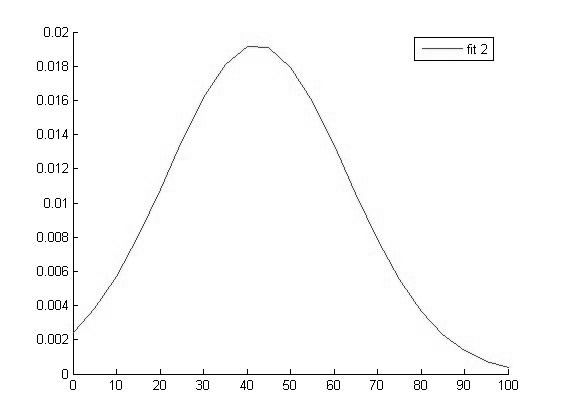График функции распределения для значений ВАШСП в 2 группе

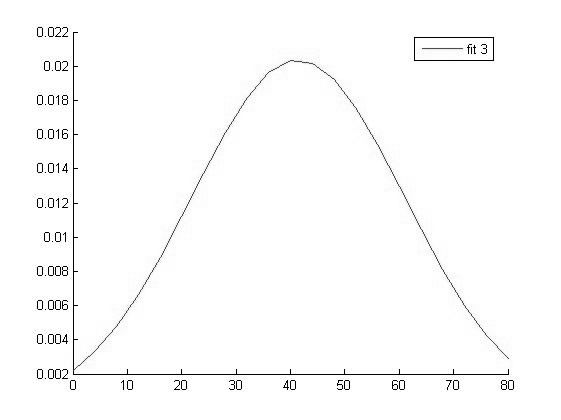График функции распределения для значений ВАШСП в 3 группе

График функции распределения для значений ВАШСП в 4 группе

Исходя из вида графиков можно сделать вывод о том что все выборки имеют нормальное распределение и следовательно мы можем использовать выбранный нами параметрический метод дисперсионного анализа.

 

I) Рассмотрим сначала влияние фактора на уровень Hb (гемоглобин):

 

Таблица1.1.1.Зависимость уровня Hb от инфекции вызвавшей заболевание

1группа	2группа	3 группа	4группа
124	114	140	124
124	142	121	130
110	156	136	127
93	170	125	130
133	119	138	138
129	128	150	122
149	163	154	160
122	135	127	104
145	120	153	121
124	120	120	131
99	106	171	127
125	130	128	109
137	156	154	158
156	114	140	132
148	137	110	134
138	142	151	164
144	121	142	116
133	121	144	136
145	144	120	122
121	160		150
126	140		112
128	110		124
120	135		137
150	106		130
123	126		160
150	136		150
160	142		107
139	118		114
152	126		124
146	140		120
142	101		115
137	123
148	117
130
152
126
118
140
166
128
165
143
132
130
126
166
168
128
126
125
115
118
117
114
123
150
125
103
142
150
140
94
129
156
141
148
140
141
135
150
150
127
158
131
150
162
134
104
130
136
150
136
105
146
146
138
158
154
141
134
150
150
114
109
157
161
133
166
168

 

Здесь и далее для экономии времени и упрощения вычислительн6ой работы воспользуемся Matlab для проведения однофакторного дисперсионного анализа для сравнения средних арифметических значений выборок. Будем использовать функцию p = anova1(X) - функция позволяет провести однофакторный дисперсионный анализ для сравнения средних арифметических значений одной или нескольких выборок одинакового объема. Выборки определяются входным аргументом Х. Х задается как матрица с размерностью mxn, где m - число наблюдений в выборке (число строк Х), n - количество выборок (число столбцов матрицы Х). Выходным аргументом функции является уровень значимости p нулевой гипотезы. Нулевая гипотеза состоит в том, что все выборки в матрице Х взяты из одной генеральной совокупности или из разных генеральных совокупностей с равными средними арифметическими. p является вероятностью ошибки первого рода, или вероятностью необоснованно отвергнуть нулевую гипотезу. Если значение p 0, то нулевая гипотеза может быть отвергнута, т.е. хотя бы одно среднее арифметическое отличается от остальных значений. Выбор критического уровня значимости p_KP для условия принятия нулевой гипотезы

 

 

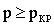
предоставлен исследователю. Здесь и далее примем p_KP равным 0,05.

После выполнения вычислений мы получаем:

p = 0.3001

Запишем выходные данные в таблицу дисперсионного анализа

 

Таблица №1.1.2. Дисперсионный анализ по одному признаку.

Компонента дисперсии	Сумма квадратов	Степень свободы	Средний квадрат
Между выборками	1012,4	3	337,451
Остаточная	30577,2	112	273,011
Полная	31589,5	115	-----

 

p>p кр

Вывод:

Следовательно мы принимаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости уровень гемоглобина в крови не зависит от инфекции вызывающей реактивный артрит.

II) Влияние фактора на наличие СРБ в крови

Таблица1.2.1.Зависимость уровня СРБ от инфекции вызвавшей заболевание

Группа

Группа

Группа

Группа

0

6

0

0

6

0

0

0

96

48

0

0

192

0

0

0

0

6

12

96

0

6

12

0

0

0

6

0

0

12

0

0

0

0

0

48

0

0

48

0

48

192

0

384

0

0

0

48

12

6

0

0

0

48

0

0

384

6

12

0

192

0

0

0

12

0

0

0

48

0

48

0

0

0

0

0

96

0

 

0

0

0

 

0

48

0

 

96

0

0

 

96

12

48

 

48

6

0

 

0

6

0

 

0

0

0

 

0

96

0

 

0

48

0

 

48

6

0

 

48

0

12

 

0

0

96

 

 

0

0

 

 

0

 

 

 

0

 

 

 

0

 

 

 

768

 

 

 

96

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

12

 

 

 

0

 

 

 

0

 

 

 

6

 

 

 

0

 

 

 

6

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

6

 

 

 

0

 

 

 

0

 

 

 

192

 

 

 

48

 

 

 

0

 

 

 

0

 

 

 

192

 

 

 

768

 

 

 

6

 

 

 

0

 

 

 

96

 

 

 

24

 

 

 

0

 

 

 

6

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

96

 

 

 

48

 

 

 

0

 

 

 

0

 

 

 

48

 

 

 

0

 

 

 

0

 

 

 

6

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

0

 

 

 

 

После выполнения вычислений мы получаем:

p =0.4677

Запишем выходные данные в таблицу дисперсионного анализа

Таблица №1.2.2. Дисперсионный анализ по одному признаку.

Компонента дисперсии	Сумма квадратов	Степень свободы	Средний квадрат
Между выборками	23192,8	3	7730,92
Остаточная	1616980,7	178	9084,16
Полная	1640173,5	181	-----

 

p>p кр

Вывод:

Следовательно, мы принимаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости уровень СРБ в крови не зависит от инфекции вызывающей реактивный артрит.

 

III) Влияние фактора на СОЭ

Таблица1.3.1.Зависимость СОЭ от инфекции вызвавшей заболевание

Группа	Группа	Группа	Группа
18	34	10	10
19	4	21	26
42	24	3	6
66	1	7	4
25	35	22	12
10	16	26	25
13	1	12	4
28	36	6	40
3	22	1	52
26	34	18	18
28	50	1	62
38	28	2	40
28	14	4	7
1	64	10	5
52	30	23	3
48	9	2	8
26	32	10	12
14	10	17	5
12	2	15	12
48	2		12
19	12		10
28	37		30
25	18		24
6	58		40
11	10		2
26	15		2
2	2		8
51	10		5
24	10		10
13	10		35
6	34		39
10	38
2	25
30
2
3
46
56
3
11
4
4
24
11
7
1
7
9
20
14
4
12
17
14
5
2
40
30
6
3
26
69
25
3
35
6
8
3
5
1
5
5
7
6
3
3
5
10
15
3
3
38
49
5
3
19
2
3
10
5
3
5
16
5
4
4
10
1
4

 

После вычислений получаем:

p = 0.0810

Таблица №1.3.2. Дисперсионный анализ по одному признаку.

Компонента дисперсии	Сумма квадратов	Степень свободы	Средний квадрат
Между выборками	1658,2	3	552,744
Остаточная	43145,7	178	242,391
Полная	44803,9	181	-----

p > p кр

 

Вывод:

Следовательно мы принимаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости СОЭ не зависит от инфекции вызывающей реактивный артрит.

 

IV) Влияние фактора на уровень Фибриногена в крови

Таблица1.4.1.Зависимость уровня фибриногена от инфекции вызвавшей заболевание

Группа	Группа	Группа	Группа
3.00	5.25	6.75	2.80
4.50	2.00	2.50	3.75
3.50	5.75	3.10	2.50
7.25	2.50	3.00	3.00
4.00	5.50	6.75	3.25
3.25	3.50	4.50	3.50
5.50	3.25	3.50	3.75
4.00	7.25	2.50	5.25
3.25	3.75	2.50	5.10
5.00	3.00	4.50	4.50
3.60	7.00	3.00	12.20
4.25	5.50	2.15	5.75
4.25	4.00	2.00	5.50
3.00	7.50	3.25	3.00
10.20	3.50	4.25	2.50
4.75	4.00	2.25	3.00
4.50	5.50	2.10	3.50
5.00	3.25	4.75	3.00
5.50	2.50	3.50	2.00
5.50	3.00		3.50
3.75	3.50		4.00
3.75	5.00		3.50
4.50	3.30		3.00
5.75	5.00		2.75
3.00	4.25		3.00
4.25	3.00		2.75
3.75	2.00		3.00
5.25	3.25		2.00
6.25	2.50		1.75
2.25	3.25		4.25
3.25	4.30		3.00
2.50	4.25
2.75	4.00
4.00
2.75
4.00
4.50
6.75
3.25
3.75
3.25
4.00
4.25
3.50
2.60
2.75
4.25
2.00
3.75
4.00
4.00
3.00
4.00
3.00
3.20
2.00
8.75
4.00
4.00
5.00
5.00
7.50
4.00
3.25
2.90
3.25
2.90
3.00
2.00
3.00
2.00
2.75
3.00
2.93
4.25
3.00
3.75
4.00
3.00
2.75
2.00
6.00
3.50
3.00
2.50
4.75
3.00
2.75
3.25
2.50
2.00
3.10
2.00
3.25
3.25
3.00
3.25
3.25
4.00

 

После вычислений получаем:

p =0.5494

Таблица №1.4.2. Дисперсионный анализ по одному признаку.

Компонента дисперсии	Сумма квадратов	Степень свободы	Средний квадрат
Между выборками	4.733	3	1.57754
Остаточная	397.546	178	2.2334
Полная	402.278	181	-----

 

p>p кр

Вывод:

Следовательно мы принимаем нулевую гипотезу. т.е. можно предположить что при 5% уровне значимости уровень фибриногена в крови не зависит от инфекции вызывающей реактивный артрит.

 

V) Влияние фактора на показатель ВАШБП

Таблица 1.5.1.Зависимость ВАШБП от инфекции вызвавшей заболевание

Группа	Группа	Группа	Группа
15	25	45	67
28	25	57	65
63	35	40	50
45	33	33	45
40	65	55	55
80	45	50	27
20	50	55	58
48	25	40	45
75	45	0	30
35	44	45	50
55	100	48	35
85	65	30	20
45	55	25	78
43	64	20	50
45	15	40	60
50	15	20	75
50	40	13	75
56	28	30	30
10	15	5	55
55	25		15
45	17		30
95	70		20
32	45		40
25	55		35
70	40		35
45	10		15
28	5		55
27	25		30
75	10		25
45	2		16
55	35		30
35	60
33	45
5
45
35
73
55
56
43
55
20
53
30
55
55
15
70
60
36
20
38
15
53
12
23
40
52
25
0
70
95
25
10
27
40
20
45
15
17
25
25
10
35
70
12
5
38
5
0
5
65
57
5
0
25
5
20
21
5
10
15
15
23
35
3
10
37

После вычислений получаем:

p = 0.4569

Таблица №1.5.2. Дисперсионный анализ по одному признаку.

Компонента дисперсии	Сумма квадратов	Степень свободы	Средний квадрат
Между выборками	1210.5	3	403.498
Остаточная	82391	178	462.871
Полная	83601.5	181	-----

 

p > p кр

 

Вывод:

Следовательно мы принимаем нулевую гипотезу. т.е. можно предположить что при 5% уровне значимости ВАШБП не зависит от инфекции вызывающей реактивный артрит.

 

VI) Влияние фактора на показатель ВАШСП

Таблица 1.6.1.Зависимость ВАШСП от инфекции вызвавшей заболевание

Группа	Группа	Группа	Группа
20	35	62	70
53	32	70	78
68	28	40	41
55	40	50	30
43	65	60	60
75	25	56	40
12	70	68	60
40	38	20	42
67	52	10	83
38	40	40	53
80	100	70	70
80	55	50	51
41	50	34	70
65	78	30	80
50	15	32	70
48	38	25	80
45	50	20	75
50	28	39	30
25	30	10	19
40	35		10
55	29		31
89	68		60
60	45		45
25	70		45
70	50		39
50	10		15
50	20		50
55	35		20
55	20		20
60	2		50
55	37		40
40	55
32	50
40
54
47
80
78
65
50
62
25
52
50
30
60
19
70
70
41
30
43
17
60
15
20
41
43
40
5
80
95
35
20
35
40
48
18
18
40
60
10
20
12
10
50
3
0
5
63
58
10
0
80
10
30
20
5
9
10
40
20
33
5
18
40
15

 

После вычислений получаем:

p = 0.3222

Таблица №1.6.2. Дисперсионный анализ по одному признаку.

Компонента дисперсии	Сумма квадратов	Степень свободы	Средний квадрат
Между выборками	1701.7	3	567.223
Остаточная	85230.9	176	484.266
Полная	86932.5	179	-----

 

p>p кр

 

Вывод:

Следовательно мы принимаем нулевую гипотезу. т.е. можно предположить что при 5% уровне значимости ВАШСП не зависит от инфекции вызывающей реактивный артрит.

В связи с тем что не один из показателей активности заболевания а также показатели ВАШ не зависят от инфекции предшествующей реактивному артриту дальнейшее разделение данных на группы можно считать не целесообразным.