Поскольку вывод передаточной функции трехфазного двигателя достаточно громоздкий, предположим, что в погружных насосах скважин используются двигатели постоянного тока. Рассчитаем параметры цифрового ПИД - регулятора такого двигателя.
Двигатель постоянного тока как динамическая система описывается следующими уравнениями в операторной форме:
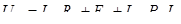 , (11.1)
, (11.1)
где 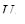 - напряжение питания двигателя;
- напряжение питания двигателя;
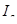 - ток якоря;
- ток якоря;
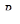 - активное сопротивление якоря;
- активное сопротивление якоря;
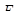 - среднее значение ЭДС вращения;
- среднее значение ЭДС вращения;
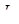 - индуктивность обмоток двигателя;
- индуктивность обмоток двигателя;
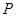 - мощность двигателя.
- мощность двигателя.
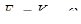 ,(11.2)
,(11.2)
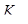 - коэффициент, зависящий от конструктивных параметров двигателя;
- коэффициент, зависящий от конструктивных параметров двигателя;
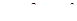 - круговая частота вращения двигателя.
- круговая частота вращения двигателя.
Выражения для электромагнитного момента:
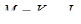 ,(11.3)
,(11.3)
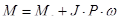 ,(11.4)
,(11.4)
где 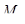 - внешний момент, или момент нагрузки;
- внешний момент, или момент нагрузки;
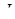 - момент инерции двигателя.
- момент инерции двигателя.
На основании этих уравнений может быть построена структурная схема двигателя как динамической системы (рисунок 11.1). Входным сигналом для этой системы является напряжение питания, выходным – круговая частота вращения двигателя. Дополнительное возмущение системы вноситься внешним моментом.
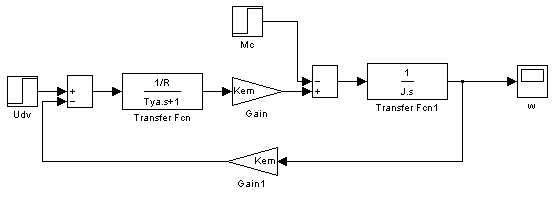
Рисунок 11.1 – Структурная схема двигателя
Из структурной схемы можно получить передаточные функции двигателя относительно круговой частоты вращения или тока:
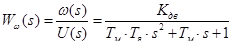 ,(11.5)
,(11.5)
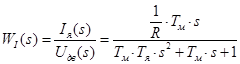 ,(11.6)
,(11.6)
где 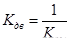 - коэффициент передачи;
- коэффициент передачи;
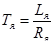 - постоянная времени якоря;
- постоянная времени якоря;
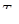 - электромеханическая постоянная времени.
- электромеханическая постоянная времени.
Рассчитаем коэффициенты цифрового ПИД - регулятора, управляющим пуском или остановом двигателя постоянного тока с конструктивными параметрами, аналогичными параметрам двигателя погружного насоса (таблица 11.1).
Таблица 11.1 – Паспортные данные двигателя постоянного тока
| Характеристика | Значение | ед. изм. |
| Номинальная мощность | 30 | кВт |
| Номинальное напряжение | 380 | В |
| Номинальный ток | 85 | А |
| Сопротивление обмотки якоря | 30 | Ом |
| Индуктивность обмотки якоря | 0,5 | Гн |
| Частота вращения | 152 | рад/с |
| Момент инерции | 0,3 | кг/см2 |
| Конструктивный параметр | 2,5 | Вс |
| Эм. постоянная времени | 6,5 |
|
Переход к передаточной функции приведенной непрерывной части двигателя осуществляется по следующей формуле:
 ,(11.7)
,(11.7)
где 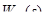 - исходная передаточная функция двигателя.
- исходная передаточная функция двигателя.
С учетом технических характеристик двигателя, его передаточные функции примут вид:
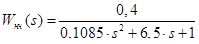 ,(11.8)
,(11.8)
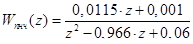 .
.
Передаточная функция цифрового ПИД регулятора имеет следующий вид:
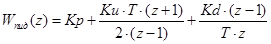 ,(11.9)
,(11.9)
где 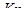 - коэффициент усиления пропорциональной составляющей;
- коэффициент усиления пропорциональной составляющей;
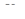 - коэффициент усиления интегральной составляющей;
- коэффициент усиления интегральной составляющей;
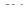 - коэффициент усиления дифференциальной составляющей;
- коэффициент усиления дифференциальной составляющей;
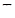 - период дискретизации (принимаем равным 0,2 с).
- период дискретизации (принимаем равным 0,2 с).
Интегральная составляющая определяется из следующего соотношения:
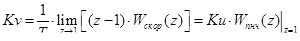 ,(11.10)
,(11.10)
где  - коэффициент добротности по скорости (выбирается произвольно в рамках от 1 до 10. В данном случае примем равным 1,2);
- коэффициент добротности по скорости (выбирается произвольно в рамках от 1 до 10. В данном случае примем равным 1,2);
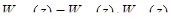 - передаточная функция скорректированной системы.
- передаточная функция скорректированной системы.
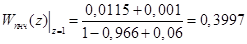 ,(11.11)
,(11.11)
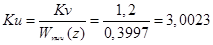 .(11.12)
.(11.12)
Остальные коэффициенты усиления цифрового ПИД регулятора можно получить из следующей системы уравнений:
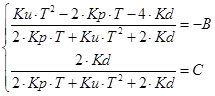 , (11.13)
, (11.13)
где B и С – коэффициенты, выбираемые из 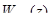 .
.
Эта система, с учетом уже известных переменных может быть представлена в виде:
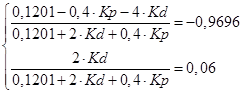 , (11.14)
, (11.14)
откуда получаем 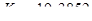 ,
, 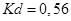 . Переходные характеристики двигателя без регулятора и с ним, представлены на рисунке 11.2. Окончательные значения коэффициентов усиления цифрового ПИД регулятора сведены в таблицу 11.2.
. Переходные характеристики двигателя без регулятора и с ним, представлены на рисунке 11.2. Окончательные значения коэффициентов усиления цифрового ПИД регулятора сведены в таблицу 11.2.
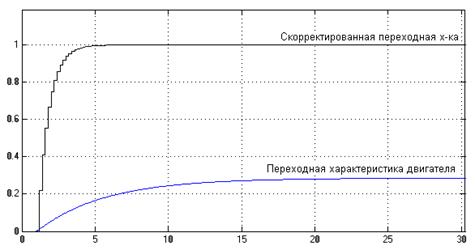
Рисунок 11.2 – Переходные характеристики двигателя с регулятором и без
Таблица 11.2 – Значения коэффициентов цифрового ПИД регулятора
| Коэффициент | Обозначение | Рассчитанное знач. | Результирующее знач. |
| Пропорциональный | Kp | 19,3852 | 19,3852 |
| Интегральный | Ku | 3,0023 | 0,30023 |
| Дифференциальный | Kd | -0,56 | -2,8 |
Дата: 2019-07-30, просмотров: 304.