Сердечники тороидальной формы

1. Обмотка на каркасе. При массивных измерениях магнитных параметров сердечников иногда используют разъемные обмотки, вмонтированные в каркас прямоугольного сечения, внутрь которого помещают тороидальные сердечники (табл. 5.).

Табл. 5. Расчет индуктивности катушек на сердечниках тороидальной формы.

Вариант геометрии сечения
Приближенные формулы
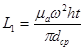
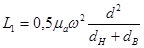
Уточненные формулы
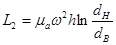
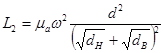
Отношение величин h, вычисленных по приближенным формулам, к величинам, вычисленным по уточненным формулам.

Связь между магнитной проницаемостью материала сердечника μ_r и индуктивностью катушки L в этом случае устанавливает формула

,

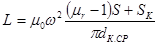где S и S_К – площади поперечных сечений сердечников и каркаса;

,

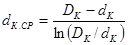где D_K и d_K – наружный и внутренний диаметры каркаса.

3. Неполная обмотка (рис. 4.).

;

;

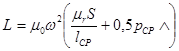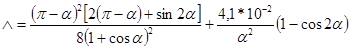где S – сечение магнитопровода; l_ср – длина средней линии магнитопровода; p_ср – периметр среднего витка.

Катушки индуктивности на разомкнутых сердечниках

Катушки на сердечниках с малыми зазорами.

Приведенные формулы справедливы при условии δ « а, где δ – ширина зазора; а – любой линейный размер поперечного сечения магнитопровода:

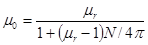; μ_r > 1;

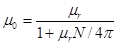 ; μ_r » 1;

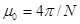; μ_r→ ∞,

где N – коэффициент размагничивания.

Сердечники с большими воздушными зазорами.

Формулы для случая малых зазоров были выведены в предположении, что поле в зазоре близко к однородному и величина потоков рассеяния пренебрежимо мала по сравнению с рабочим потоком. Если же магнитопровод содержит воздушный зазор, для которого не выполняется условие δ « а, то с целью сохранения формы записи соотношений для расчета магнитной цепи, справедливых при малых зазорах, целесообразно ввести понятие об эквивалентном зазоре.

Наиболее удобным, оказалось, определить эквивалентный зазор как такой, который имеет ту же проводимость, что и реальный; а геометрия его определяется сечением полюсов магнитопровода и некоторой эквивалентной длиной δ_Э. при этом все формулы для сердечников с зазором остаются справедливыми при подстановке в них δ_Э вместо δ.

На практике часто встречаются полюса магнитопровода в виде двух прямоугольных призм, расположенных друг против друга. Выражение для δ_Э в этом случае имеет вид

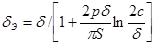
(обмотка не перекрывает зазора) или

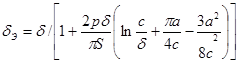
(обмотка перекрывает зазор), где δ – геометрическая длина зазора; p – периметр сечения магнитопровода у зазора; S – сечение магнитопровода у зазора (т. е. сечение полюса); 2с – высота обмотки; а – расстояние от сердечника до средней линии продольного сечения обмотки (т. е. приближенно полуширина обмотки).