Рассмотрим формулы для расчета индуктивности элементов, для которых магнитная проницаемость равна проницаемости окружающего пространства. Под общим названием «тела специальной формы» объединены элементы, не являющиеся катушками в собственном смысле, но входящие в состав цепей РЭА (провода, электроды, кабели и т. д.). Предполагается, что проводники выполнены из немагнитного материала.
Все линейные размеры приведены в сантиметрах, индуктивность в микрогенри.
Однослойная воздушная катушка со сплошной намоткой.
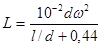 при
при 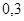 <
< 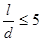 ,
,
где d – диаметр катушки; l – длина катушки; ω – число витков катушки;
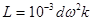 при
при 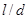 > 5.
> 5.
Многослойная воздушная катушка:
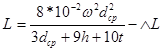 ;
;
где dср – средний диаметр катушки; h – высота катушки; t – радиальная ширина намотки; ∆ L – поправка на заполнение:
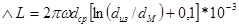 ,
,
где dиз – диаметр провода в изоляции; dм – диаметр провода по меди.
Катушка со спиральной намоткой ленточным проводом.
Расчет индуктивности практически совпадает с расчетом L для многослойной катушки с теми же наружным и внутренним диаметрами, высотой и коэффициентом заполнения. Вместо числа витков в формулу подставляют число слоев ленточной катушки.
Соленоид на каркасе прямоугольного сечения:
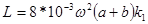 при
при 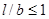 ;
;
a, b – стороны поперечного сечения каркаса, a < b; l – длина катушки; k1 - на рис 1;
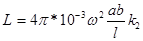 при
при 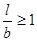 ;
;
где 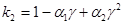 ;
; 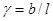 .
.
Значение поправок α1 и α2 приведены в таблице 1.
Табл. 1. Значения поправок α1 и α2.
| a/b | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
| α1 | 0,112 | 0,183 | 0,238 | 0,285 | 0,325 | 0,361 | 0,393 | 0,422 | 0,449 | 0,473 |
| α2 | 0,016 | 0,032 | 0,048 | 0,064 | 0,080 | 0,096 | 0,111 | 0,127 | 0,143 | 0,159 |
Погрешность расчетов индуктивности для l / b ≥ 1 определяют по рисунку 2, где ε – верхняя оценка относительной погрешности.
Для некоторых сочетаний l / b и a / b значения k2 приведены на рис. 3.
Плоские катушки со спиральной намоткой
1. Катушка с круглыми витками:
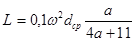 при
при 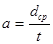 ;
;
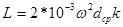 при
при 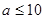 ,
,
где dср – средний диаметр намотки; t – радиальная ширина намотки; k – на рис. 4.
2. Катушка с квадратными витками:
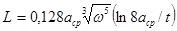 ,
,
где aср – дли средней стороны квадрата.
3. Поправка на шаг намотки
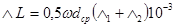 ;
;
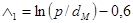 ,
,
где p – шаг намотки; dM – диаметр провода по меди (или диаметр равновеликого сечения); ∆2 – в табл. 2.
Табл. 2. Формулы для расчета поправок ∆1 и ∆2
для ленточных проводов.
| Вид провода | ∆1 | ∆2 |
| Тонкая лента (с ≤ 0,1 b) Лента квадратного сечения (b = c) |
ln 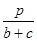 - k
значение k по графику - k
значение k по графику
| k – 2 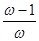 n + n + 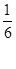 ( ( 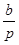 )2 *(0,6 – )2 *(0,6 – 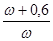 )+ + )+ + 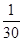 * ( * ( 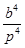 - 2,5 - 2,5 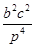 ) (0,08 - ) (0,08 - 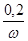 )
значения n по графику
k – 2 )
значения n по графику
k – 2 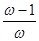 m – 0,2 ( m – 0,2 ( 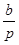 )4 * (0,08 - )4 * (0,08 - 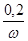 ),
значение m ),
значение m
|
Плоские контуры:
1. Круговое кольцо из провода кругового сечения:
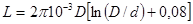 ,
,
где D – диаметр кольца по центру сечения; d – диаметр провода.
2. Круговое кольцо из провода квадратного сечения:
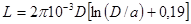 ;
;
где a – сторона поперечного сечения провода.
При высоких частотах
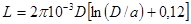 .
.
3. Круговое кольцо из тонкой ленты:
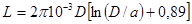 ,
,
где а – ширина ленты.
4. Контур в виде правильного многоугольника (при условии, что длина провода значительно больше периметра его сечения):
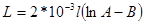 ,
,
где l – длина провода; A = 4l / d – для круглого провода с диаметром d; A = 2 l / (a + b) – для провода прямоугольного сечения со сторонами а и b; В – коэффициент, зависящий от числа сторон n. Его значения в табл. 3.
Табл. 3. Зависимость коэффициента В от числа сторон многоугольника n.
| N | 3 | 4 | 5 | 6 | 8 |
| B | 3,197 | 2,853 | 2,712 | 2,636 | 2,561 |
Формулой можно воспользоваться также для расчета индуктивности кругового витка, принимая В = 2,451.
Одиночный прямолинейный провод:
1. Провод кругового сечения.
На низких частотах
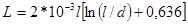 , при
, при 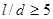 ,
,
где l – длина провода; погрешность расчета по формуле не более 5%.
При высоких частотах
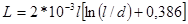 , при
, при 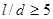 ,
,
погрешность формулы не более 6%.
2. Провод прямоугольного сечения.
На низких частотах
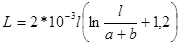 ,
,
где a, b – стороны поперечного сечения провода.
Приближенно на высоких частотах
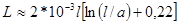 при
при 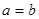 ;
;
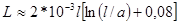 при
при 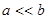 .
.
3. Полый провод круглого сечения:
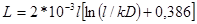 ,
,
где D – наружный диаметр провода; d – внутренний диаметр провода; k – коэффициент, значения которого в табл. 3.
Табл. 3. Зависимость k от географических размеров катушки.
| d / D | 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
| k | 0,779 | 0,782 | 0,793 | 0,809 | 0,829 | 0,852 |
| d / D | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
| k | 0,878 | 0,906 | 0,936 | 0,967 | 1,000 |
На высоких частотах формула остается справедливой, если принять k = 1.
4. Полый провод квадратного сечения.
На низких частотах
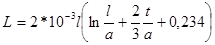 .
.
На высоких частотах
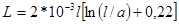 ,
,
где l – длина провода; а – внешняя сторона контура поперечного сечения; t - толщина стенки ( 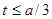 ).
).
Система прямолинейных проводов:
1. Два параллельных провода (прямой и обратный):
а) для проводов круглого сечения одинакового диаметра на низких частотах
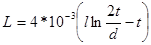 .
.
На высоких частотах
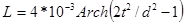 ,
,
где t – расстояние между осями проводов; d – диаметр провода; l – длина провода.
б) для одинаковых проводов прямоугольного сечения на низких частотах
L = 4*10-3 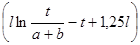 ,
,
где t – расстояние между центрами сечений; a и b – стороны сечения.
в) для проводов различных сечений
L = L1 + L2 – 2M,
где L1 и L2 – индуктивности каждого провода; М – взаимная индуктивность.
2. Проводник – земля. Индуктивность определяют по формулам параллельных проводов; значение ее вдвое меньше, чем вычисленное для системы прямого и обратного проводов при t = 2h (h – расстояние до поверхности земли).
Формулы справедливы при h » λ3 (λ3 – длина электромагнитных колебаний в земле).
Для приближенных расчетов
L = 2*10-3 l 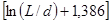 .
.
3. Коаксиальный кабель:
L = 2*10-3 l 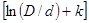 ,
,
где l – длина кабеля; D – внутренний диаметр наружного цилиндра; d – внешний диаметр внутреннего цилиндра; k – коэффициент, зависящий от частоты.
4. Пучок равноудаленных параллельных проводов (ориентировочно):
L= 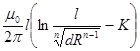 ,
,
где n – число проводов; d – диаметр отдельного провода; R – радиус размещения проводов (расстояние от центра пучка до центра любого провода);
K = 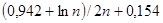 .
.
Значение К в зависимости от числа проводов n приведены в табл. 4
Табл. 4. Зависимость К от числа проводов n.
| n | 2 | 3 | 4 | 5 | 7 | 10 | 12 | 15 |
| K | 0,56 | 0,49 | 0,44 | 0,41 | 0,36 | 0,31 | 0,30 | 0,28 |
Конденсаторные секции.
1. Плоская конденсаторная секция:
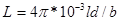 ,
,
где l – длина электрода; d – толщина диэлектрода; b – ширина диэлектрода.
Предполагается, что b»d»a (а – толщина электрода).
Если имеет место только неравенство d«b»a, то
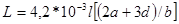 .
.
2. Плоская конденсаторная секция, состоящая из нескольких параллельно соединенных элементов:
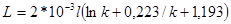 ,
,
где l – длина секции (в направлении между торцами обкладок); 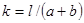 , где a и b – ширина и толщина секции.
, где a и b – ширина и толщина секции.
3. Цилиндрическая намотанная секция с выступающими обкладками (так называемая безындукционная намотка). Расчет индуктивности можно проводить по формуле для провода круглого сечения, принимая, что l – длина секции (в направлении между торцами обкладок), d – наружный диаметр секции.
Провод кругового сечения, изогнутый по дуге окружности:
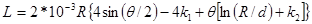 ,
,
где R – радиус окружности, по дуге которой изогнут провод; Ө - центральный угол, соответствующий длине провода; 0≤Ө≤2π; d – диаметр провода; k1 – коэффициент, которого на рис. 4; k2 = 1,02 для низких и средних частот; k2 = 0,77 для высоких частот.
В частном случае, когда
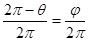 «1,
«1,
Дата: 2019-07-30, просмотров: 253.