Рассмотрим типы проводимости полупроводников с энергетической точки зрения, для чего воспользуемся энергетическими зонами.

 W 3
W 3 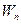 W
W 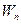
3

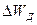
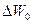
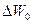
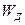
2 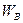 2
2 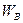
1 x 1 x
а в
W 


 _ W
_ W
3 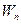 3
3 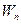


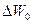
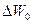
2 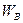 2
2 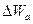
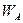
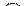


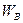
+
1 x 1 x
б г
Рисунок 4 (а-г) – Диаграмма энергетических уровней полупроводника
Электрон отдельного атома характеризуется разрешенными уровнями энергии, на которых он может находиться. В кристалле уровни энергии электронов объединяются в энергетические зоны. По оси ординат диаграммы (рис. 4) откладывается энергия электронов, выражаемая в электрон-вольтах, а по оси абсцисс откладывается расстояние от выбранного в какой-либо точке тела начала координат. Энергетических зон имеется три: зона валентных связей или валентная зона 1, зона проводимости 3 и запрещенная зона 2 (рис 4 а).
Зона валентных связей соответствует электронам с более низкими энергетическими уровнями, так как валентные электроны находятся вблизи от атомов и связаны с ними ковалентными связями.
Зона проводимости включает в себя энергетические уровни электронов, освободившихся от атомов, и поэтому энергетические уровни этой зоны выше энергетических уровней валентной зоны.
Запрещенная зона не имеет энергетических уровней энергии. Она отделяет валентную зону от зоны проводимости. Запрещенная зона характеризуется так называемой шириной запрещенной зоны, которая определяется как разность энергетических уровней: нижнего уровня зоны проводимости 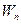 и верхнего уровня валентной зоны
и верхнего уровня валентной зоны 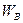 , т.е.
, т.е. 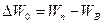 .
.
Необходимо отметить, что понятие об энергетических зонах чисто условное и что в самом полупроводнике не имеется каких-либо зон, ограниченных геометрическими размерами. Энергетические уровни и энергетические зоны явились удобной формой для определения электрических свойств полупроводника.
Проводимость беспримесного полупроводника. На рис. 4 б показана диаграмма энергетических уровней полупроводника собственной проводимости. Для того, чтобы монокристалл стал токопроводящим, необходимо повысить энергетический уровень валентного электрона, т.е. перевести его в зону проводимости, для чего электрону необходимо сообщить добавочную энергию (энергию диссоциации) не меньше 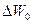 . На рисунке переход электрона из валентной зоны в зону проводимости показан стрелкой .
. На рисунке переход электрона из валентной зоны в зону проводимости показан стрелкой .
После перехода электрона из валентной зоны в кристаллической решетке полупроводника остается незаполненный энергетический уровень, т.е. образуется дырка. Дырка представляет собой подвижный положительный заряд, который под влиянием электрического поля перемещается в валентной зоне по направлению силовых линий поля, т.е. навстречу электрону в зоне проводимости. Таким образом, ток, протекающий в беспримесном полупроводнике, состоит из электронов, перемещающихся в зоне проводимости, и дырок, перемещающихся в заполненной зоне.
Проводимость полупроводника с донорной примесью (проводимость типа n). На рис. 4 в изображена энергетическая диаграмма такого полупроводника. Энергетические уровни атомов доноров 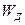 расположены в запрещенной зоне вблизи зоны проводимости. Электроны донорной примеси, для того чтобы попасть в зону проводимости, должны получить дополнительно энергию
расположены в запрещенной зоне вблизи зоны проводимости. Электроны донорной примеси, для того чтобы попасть в зону проводимости, должны получить дополнительно энергию 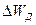 , которая называется энергией активации и равна разности между уровнем энергии электронов нижнего участка зоны проводимости и уровнем энергии донорной примеси, т.е.
, которая называется энергией активации и равна разности между уровнем энергии электронов нижнего участка зоны проводимости и уровнем энергии донорной примеси, т.е.  . Поскольку энергия активации значительно меньше энергии диссоциации (
. Поскольку энергия активации значительно меньше энергии диссоциации ( 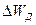 =0,01-0,05 эВ), то поставщиком электронов в зону проводимости будут избыточные электроны донорной примеси, а проводимость полупроводника будет преимущественно электронной (типа n). Лишь небольшая часть валентных электронов преодолеет ширину запрещенной зоны
=0,01-0,05 эВ), то поставщиком электронов в зону проводимости будут избыточные электроны донорной примеси, а проводимость полупроводника будет преимущественно электронной (типа n). Лишь небольшая часть валентных электронов преодолеет ширину запрещенной зоны 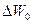 и из валентной зоны перейдет в зону проводимости, создав одновременно небольшое количество дырок.
и из валентной зоны перейдет в зону проводимости, создав одновременно небольшое количество дырок.
Атомы доноров после ухода от них электронов в зону проводимости превращаются в положительные неподвижные ионы.
Проводимость полупроводника с акцепторной примесью (проводимость типа p). На рис. 4 г изображена энергетическая диаграмма дырочного полупроводника. Энергетические уровни акцепторной примеси WA расположены в запрещенной зоне ближе к зоне валентных связей. Поскольку энергия активации акцепторной примеси 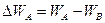 значительно меньше ширины запрещенной зоны, то «поставщиком» электронов на уровни акцепторной примеси будет валентная зона. Атом акцепторной примеси, приняв электрон, превращается в отрицательный ион, а подвижными носителями тока будут дырки, перемещающиеся в валентной зоне. Проводимость полупроводника будет преимущественно дырочной и лишь в малой степени электронной за счет некоторых электронов валентной зоны, преодолевших ширину запрещенной зоны и перешедших на энергетические уровни зоны проводимости.
значительно меньше ширины запрещенной зоны, то «поставщиком» электронов на уровни акцепторной примеси будет валентная зона. Атом акцепторной примеси, приняв электрон, превращается в отрицательный ион, а подвижными носителями тока будут дырки, перемещающиеся в валентной зоне. Проводимость полупроводника будет преимущественно дырочной и лишь в малой степени электронной за счет некоторых электронов валентной зоны, преодолевших ширину запрещенной зоны и перешедших на энергетические уровни зоны проводимости.
С повышением температуры электропроводимость полупроводников возрастает, а сопротивление уменьшается. Это происходит вследствие того, что число электронов, перебрасываемых из валентной зоны в зону проводимости увеличивается, а следовательно, увеличивается и число дырок в валентной зоне.
Зависимость сопротивления R полупроводников от температуры Т в определенных температурных интервалах описывается выражением
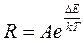 ,
,
где А – константа, зависящая от природы полупроводника и слабо зависящая от температуры;
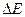 - энергия активации, это энергия, которую надо сообщить электрону, чтобы он мог преодолеть запретную зону;
- энергия активации, это энергия, которую надо сообщить электрону, чтобы он мог преодолеть запретную зону;
к – постоянная Больцмана;
к = 
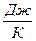 ;
;
е – основание натурального логарифма.
Описание установки
Лабораторная установка состоит из термистора, помещенного в электронагреватель и соединенного с омметром.
Температура термистора измеряется термометром.

термометр
термистор
Электронагреватель
к омметру
Рисунок 5 – Схема лабораторной установки
Порядок выполнения работы
1. Измерить сопротивление термистора при комнатной температуре и занести в таблицу.
2. Включив электронагреватель, измерять сопротивление R термистора через каждые 100С до 800С.
3. Данные эксперимента занести в таблицу.
4. Построить график зависимости 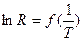 .
.
5. Найти тангенс угла наклона графика (график представляет собой прямую) к оси 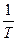 (ось х).
(ось х).
6. По формуле 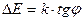 определить энергию активации.
определить энергию активации.
Таблица 1. Результаты измерений и расчетов
| № опыта | t,0C | T, K | 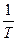 , K-1 , K-1
| R, Ом | lnR |
Контрольные вопросы
1. Расскажите о собственной и примесной проводимости полупроводников на основе классических представлений и зонной теории.
2. Запишите и поясните, по какому закону изменяется сопротивление полупроводников с изменением температуры.
3. Что такое энергия активации?
Литература [ 3,6,7]
ЧАСТЬ V
ФИЗИКА АТОМА И АТОМНОГО ЯДРА
Любое физическое тело состоит из мельчайших частиц, называемых атомами. Опытами Резерфорда (1911 г.) было установлено, что атом любого химического элемента состоит из положительно заряженного ядра, вокруг которого вращаются по круговым орбитам электроны.
Атомное ядро состоит из нейтронов и протонов. Нейтрон не имеет заряда, он электрически нейтрален. Протон обладает единичным положительным зарядом, равным по величине заряду электрона. В нормальном состоянии атома число электронов в его оболочке равно числу протонов в его ядре.
Число положительных зарядов ядра, равное числу протонов, входящих в его состав, называется атомным номером элемента Z. Суммарное число протонов и нейтронов в атомном ядре называют массовым числом А элемента. Так как число протонов в ядре равно Z, то число нейтронов равно А – Z. Массовое число равно ближайшему целому числу, выражающему атомный вес элемента.
Атомы, имеющие один и тот же атомный номер, но разные массовые числа, называют изотопами. Химически они тождественны и представляют собой разновидности одного и того же химического элемента.
Изотопы каждого химического элемента разделяются на стабильные и неустойчивые. Ядра неустойчивых изотопов претерпевают самопроизвольный распад, превращаясь при этом в ядра атомов других элементов. Такие изотопы называются радиоактивными.
В процессе распада ядра атомов испускают радиоактивное излучение трех типов: 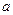 ,
, 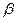 , и
, и 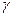 - излучение.
- излучение.
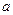 - излучение представляет собой поток ядер гелия
- излучение представляет собой поток ядер гелия 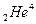 ;
;
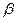 - излучение – поток электронов
- излучение – поток электронов 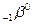 или позитронов
или позитронов  ;
;
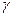 - излучение – электромагнитное излучение с очень короткой длиной волны, аналогичное жестким рентгеновским лучам.
- излучение – электромагнитное излучение с очень короткой длиной волны, аналогичное жестким рентгеновским лучам.
Рассмотрим электрон, движущийся в поле атомного ядра с зарядом 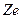 . При Z = 1 такая система соответствует атому водорода, при иных Z – водородоподобному иону. Кулоновская сила взаимодействия
. При Z = 1 такая система соответствует атому водорода, при иных Z – водородоподобному иону. Кулоновская сила взаимодействия 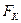 между ядром и электроном сообщает электрону нормальное ускорение.
между ядром и электроном сообщает электрону нормальное ускорение.
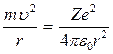 или
или  , (1)
, (1)
где 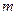 - масса электрона;
- масса электрона;
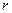 - радиус орбиты;
- радиус орбиты;
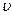 - скорость электрона.
- скорость электрона.
Полная энергия Е электрона складывается из кинетической и потенциальной энергий:
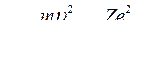 (2)
(2)
Подставив выражение (1) в (2), получим выражение для полной энергии электрона:
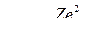 (3)
(3)
Согласно электромагнитной теории вращающийся по орбите электрон возбуждает вокруг себя переменное электромагнитное поле, распространяющееся в пространстве со скоростью света. Это означает, что вращение электрона должно вызвать непрерывное излучение, на которое электрон затрачивает часть своей энергии. Таким образом, согласно классической теории, энергия электрона все время уменьшается. Из формулы (3) следует, что меньшему значению энергии (с учетом знака) соответствует меньший радиус. В результате электрон должен упасть на ядро. В действительности атом является устойчивой системой. Из формулы (1) следует, что с уменьшением радиуса орбиты, скорость движения электрона возрастает, т. е. период обращения уменьшается. Это должно привести к непрерывному увеличению частоты излучаемых электромагнитных волн, и атом должен излучать сплошной спектр. Однако, в действительности, атом может излучать лишь линейчатый спектр. Выход из создавшегося положения был предложен Бором (1913). Основываясь на гипотезе Планка о квантовом характере излучения и поглощения света, Бор сформулировал законы движения электрона в атоме в виде трех постулатов, которые дали объяснения экспериментальным фактам:
1. Электрон в атоме может вращаться только по таким орбитам, на которых момент количества движения электрона равен целому кратному от 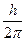 (такие орбиты называются стационарными):
(такие орбиты называются стационарными):
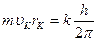 , (4)
, (4)
где 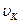 - скорость электрона на к–той орбите;
- скорость электрона на к–той орбите;
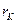 - радиус к –той орбиты;
- радиус к –той орбиты;
к = 1, 2, 3, … - квантовые числа, определяющие принадлежность электрона к той или иной орбите;
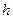 - постоянная Планка.
- постоянная Планка.
2. Вращаясь по стационарной орбите, электрон не излучает и не поглощает энергию.
3. Излучение или поглощение энергии происходит лишь при переходе электрона с одной стационарной орбиты на другую стационарную орбиту. Если электрон переходит с внешних орбит на внутренние, то излучается квант света, частота 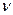 которого определяется из условия:
которого определяется из условия:
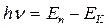 , (5)
, (5)
где 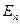 и
и 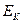 - энергии электрона на
- энергии электрона на 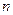 - ной и к – той орбитах (
- ной и к – той орбитах ( 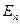 >
> 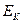 ).
).
Найдем выражения для радиусов стационарных орбит и полной энергии электрона. Возводя в квадрат обе части выражения (4) и решая совместно с уравнением (1), получим:

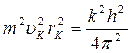
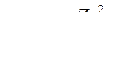
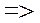
 (6)
(6)
Подставив выражение (6) в формулу (3), получим выражение для полной энергии электрона:
 (7)
(7)
Из формулы (7) следует, что квантовое число 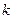 определяет энергию электрона в атоме, так как остальные величины остаются постоянными.
определяет энергию электрона в атоме, так как остальные величины остаются постоянными.
По третьему постулату Бора при переходе электрона из стационарного состояния, характеризуемого квантовым числом 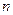 , в состояние с квантовым числом
, в состояние с квантовым числом 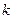 (
( 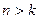 ) атом излучает свет с частотой
) атом излучает свет с частотой 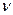 :
:
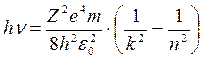
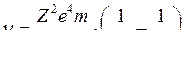 или, так как
или, так как  ,
,
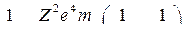 (8)
(8)
Множитель, стоящий перед скобкой, называется постоянной Ридберга и обозначается буквой 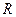 :
:
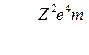 (9)
(9)
Тогда формула (8) примет простой вид:
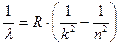 (10)
(10)
Формула (10) называется обобщенной формулой Бальмера и является одной из наиболее точных формул физики. Из нее следует, что все линии спектра могут быть объединены в серии. Серией называется совокупность линий, описываемых этой формулой, если 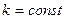 , т.е. серия возникает при переходе электрона с вышележащих орбит на орбиту с данным квантовым числом
, т.е. серия возникает при переходе электрона с вышележащих орбит на орбиту с данным квантовым числом 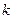 . В спектре атома водорода имеется несколько серий:
. В спектре атома водорода имеется несколько серий:
серия Лаймана к = 1, 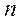 = 2, 3, 4, ... (ультрафиолетовая часть спектра)
= 2, 3, 4, ... (ультрафиолетовая часть спектра)
серия Бальмера к = 2, 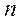 = 3, 4, 5, …(видимая часть спектра)
= 3, 4, 5, …(видимая часть спектра)
 серия Пашена к = 3,
серия Пашена к = 3, 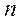 = 4, 5, …
= 4, 5, …
серия Брэкета к = 4, 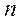 = 5, 6, … инфракрасное излучение
= 5, 6, … инфракрасное излучение
серия Пфунда к = 5, 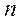 = 6, 7, …
= 6, 7, …
Видимая часть линейчатого спектра водорода (серия Бальмера) состоит из ряда линий, наиболее яркими из которых являются: красная ( 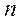 = 3); голубая (
= 3); голубая ( 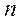 = 4); синяя (
= 4); синяя ( 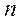 = 5); фиолетовая (
= 5); фиолетовая ( 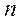 = 6). Схематически серии линий показаны на рис. 1.
= 6). Схематически серии линий показаны на рис. 1.
Несмотря на удачное объяснение спектральных закономерностей водорода и водородоподобных атомов, теория Бора обладает рядом недостатков. В частности, она не может объяснить спектры излучения более сложных атомов и различную интенсивность спектральных линий. Эти трудности были преодолены квантовой теорией, показавшей неприменимость классических представлений к микрообъектам.






 E n = 6
E n = 6





 n = 5
n = 5

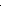

 n = 4
n = 4

 n = 3
n = 3
 n = 2
n = 2
 n = 1
n = 1
Рисунок 1 – Схема серий линий спектра водорода
ЛАБОРАТОРНАЯ РАБОТА № 35
Дата: 2019-07-24, просмотров: 417.