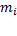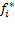Под вероятностью безотказной работы обьекта понимается вероятность того, что в пределах заданной наработки отказ обьекта не возникнет.
Вероятность безотказной работы вычисляется как отношение числа работоспособных обьектов (систем) к концу наработки на общее число всех систем, которые заданы в начале испытаний.
P(t)=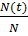 
(3.1)
Где: N(t)- число работоспособных;
N- число всех обьектов.
| P(t)1=385/390=0,9872 | P(t)7=303/390=0,7769 |
| P(t)2=377/390=0,9667 | P(t)8=296/390=0,7590 |
| P(t)3=365/390=0,9359 | P(t)9=287/390=0,7359 |
| P(t)4=348/390=0,8923 | P(t)10=272/390=0,6974 |
| P(t)5=328/390=0,8410 | P(t)11=253/390=0,6487 |
| P(t)6=314/390=0,8051 | P(t)12=230/390=0,5897 |
Вероятность отказа – это вероятность того, что обьект откажет хотя бы один раз в течении заданной наработки, будучи работоспособным в начальный момент времени.
Число работоспособных элементов можно выразить: N(t) = N – m(t), тогда получаем следующее
P(t)= 1-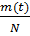 
→ Q(t)= 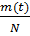(3.2)
Где: m(t)- количество элементов, отказавшихся к моменту времени t;
N-число наблюдаемых элементов;
Q(t)- вероятность отказа.
ВБР и ВО являются противоположными событиями.
P(t) + Q(t) =1 (3.3)
| Q(t)1=1-0,9872=0,0128 | Q(t)7=1-0,7769=0,2231 |
| Q(t)2=1-0,9667=0,0333 | Q(t)8=1-0,7590=0,2410 |
| Q(t)3=1-0,9359=0,0641 | Q(t)9=1-0,7359=0,2641 |
| Q(t)4=1-0,8923=0,1077 | Q(t)10=1-0,6974=0,3026 |
| Q(t)5=1-0,8410=0,1590 | Q(t)11=1-0,6487=0,3513 |
| Q(t)6=1-0,8051=0,1949 | Q(t)12=1-0,5897=0,4103 |
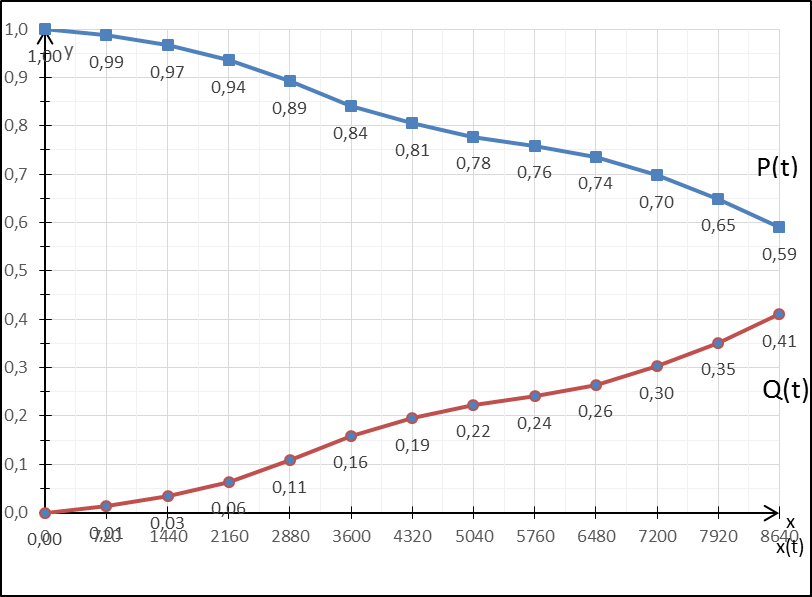
Рисунок 4. Убывающая и возрастающая линии
Глава 4. Плотность распределения отказов
ПРО- отношение числа отказавших в течении определенного времени на произведение общего числа систем на интервал времени.
fi ( t ) =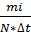 
(4.1)
N=390
∆t=720ч
| f*1=5/280800=0,000018 | f*7=11/280800=0,000039 |
| f*2=8/280800=0,000028 | f*8=7/280800=0,000025 |
| f*3=12/280800=0,000043 | f*9=9/280800=0,000032 |
| f*4=17/280800=0,000061 | f*10=15/280800=0,000053 |
| f*5=20/280800=0,000071 | f*11=19/280800=0,000068 |
| f*6=14/280800=0,000050 | f*12=23/280800=0,000082 |
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| ∆t | 0-1080 | 1080-2160 | 2160-3240 | 3240-4320 | 4320-5400 | 5400-6480 | 6480-7560 | 7560-8640 | 8640-9720 | 9720-10800 | 10800-11880 | 11880-12960 | |
|
| 5 | 8 | 12 | 17 | 20 | 14 | 11 | 7 | 9 | 15 | 19 | 23 | |
|
| 0,000018 | 0,000028 | 0,000043 | 0,000061 | 0,000071 | 0,000050 | 0,000039 | 0,000025 | 0,000032 | 0,000053 | 0,000068 | 0,000082 |
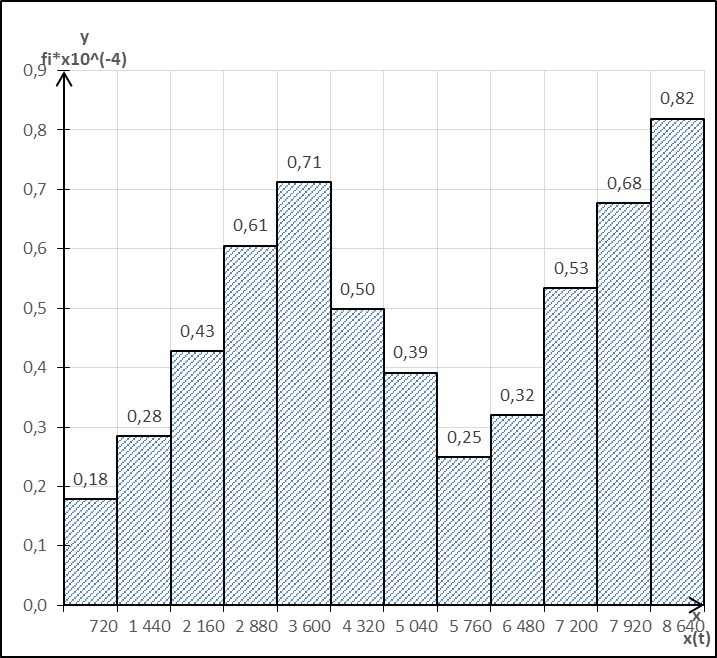
Рисунок 5. Гистограмма плотности распределения отказов
Глава 5. Интенсивность отказов
Интенсивность отказов - это условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не возник.
ИО вычисляется как отношение числа отказавших объектов в течении определенного времени на число безотказно проработавших систем на интервал времени.
Λ(t)=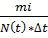 
(5.1)
| λ*1=5/(385*720)=0,000018 | λ *7=11/(303*720)= 0,000050 |
| λ *2=8/(377*720)=0,000029 | λ *8=7/(296*720)= 0,000033 |
| λ *3=12/(365*720)= 0,000046 | λ *9=9/(287*720)= 0,000044 |
| λ *4=17/(348*720)= 0,000068 | λ *10=15/(272*720)= 0,000077 |
| λ *5=20/(328*720)= 0,000085 | λ *11=19/(253*720)= 0,000104 |
| λ *6=14/(314*720)= 0,000062 | λ *12=23/(230*720)= 0,000139 |
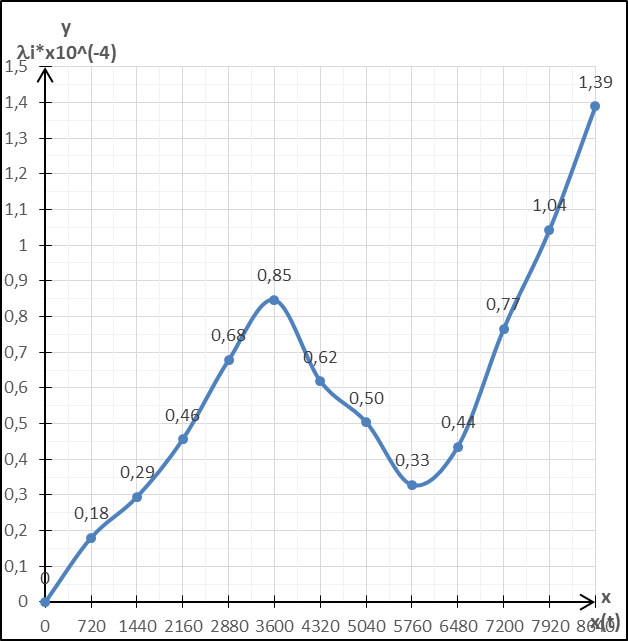
Рисунок 6. Интенсивность отказов
Глава 6. Наработка на отказ
Среднее значение безотказной работы (средняя наработка на отказ) То- для невосстанавливаемых (неремонтируемых) систем – это математическое ожидание времени работы системы до отказа.
Тt<t1= M =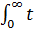 
* f(t)dt = - 
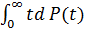(6.1)
Пределы несобственного интеграла изменяются от 0 до ꝏ, так как время не может быть отрицательным;
F(t) – есть плотность вероятности возникновения отказов системы или ее невосстанавливаемого элемента;
P(t) – есть вероятность безотказной работы в интервале времени 0<t<T.
В начальной момент времени вероятность P(t) равна единице. Вероятность P(t) связана с плотностью вероятности возникновения отказов системы или ее невосстанавливаемого элемента следующим образом:
f ( t )= -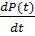 
(6.2)
Проинтегрировав выражение для Т по частям, получим:
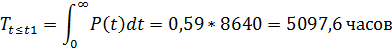
| P(t) |
| X(t) |
| СПГН |
| СПН |
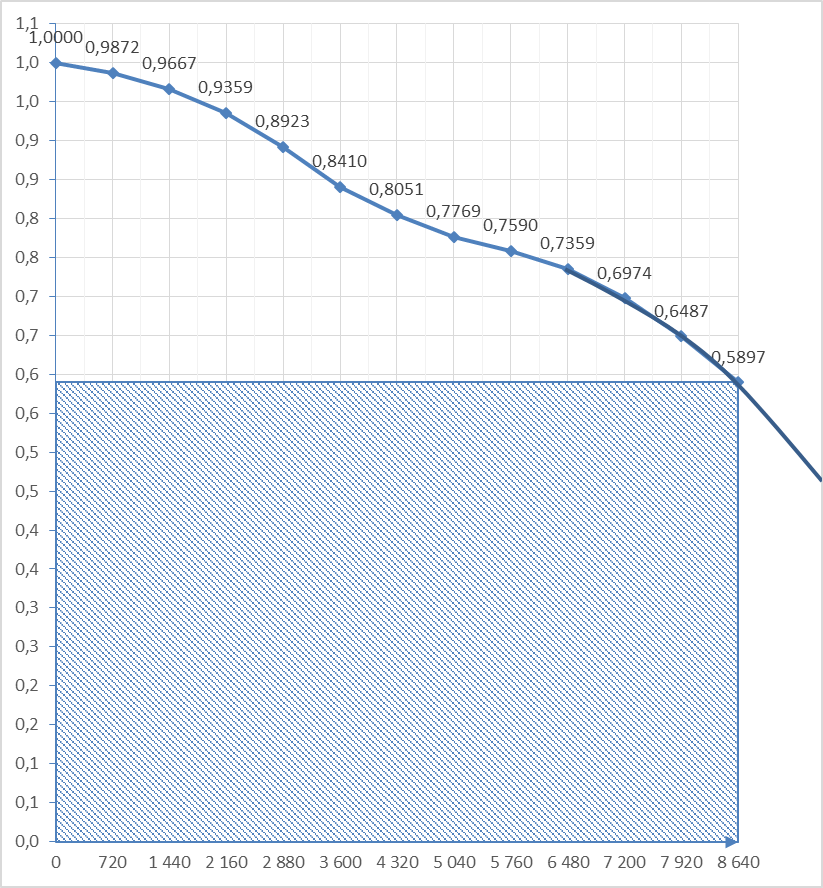
Рисунок 7. Наработка на отказ.
Дата: 2019-07-24, просмотров: 220.
