МИНИСТЕРСТВО КУЛЬТУРЫ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего и послевузовского профессионального образования
ВСЕРОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КИНЕМАТОГРАФИИ имени С.А. ГЕРАСИМОВА
СЕРГИЕВО-ПОСАДСКИЙ ФИЛИАЛ
КОНСПЕКТ ЛЕКЦИЙ
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
Часть 3
Несинусоидальные колебания.
Трёхфазный ток
для специальности среднего профессионального образования
070208
«Театральная и аудиовизуальная техника (по видам)»
(углублённая подготовка)
Сергиев Посад
2015
Рассмотрено на заседании Утверждаю:
предметной комиссии заместитель директора по УР
протокол № от Л.Г. Зуденкова
председатель ПК
М. П. Лебедь
Разработал преподаватель М.П. Лебедь
Рецензент: преподаватель Н.Л. Новинский
Вступление
Третья часть является продолжением первой и второй частей конспекта лекций по курсу "Основы электротехники" и включает в себя материал по разделам "Несинусоидальные колебания" и "Трёхфазный ток".
В работу включён минимально необходимый для сдачи экзамена объём материала. Теоретический материал иллюстрирован примерами решения задач.
Нумерация рисунков и примеров решения задач в тексте продолжает нумерацию предыдущих частей.

конспекта лекций по курсу основы электротехники
Несинусоидальные колебания
Основные понятия
В электротехнике и в электронике широко применяются колебания, форма которых отличается от синусоиды. Любое такое колебание относится к несинусоидальным.
Рассмотрим некоторые, часто встречающиеся формы несинусоидальных колебаний:
1) Пульсирующее напряжение. Встречается в выпрямителях, преобразующих синусоидальное напряжение в постоянное.
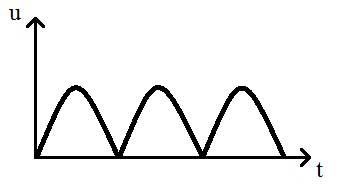
Рис. 71. Пульсирующее напряжение
В отличие от синусоидального колебания, пульсирующее изменяется только по величине, но не изменяется по направлению. Пульсирующее напряжение не меняет своей полярности, а синусоидальное меняет полярность при смене полупериода.
2) Пилообразное колебание. Используется при формирования изображения в электронно-лучевых трубках.
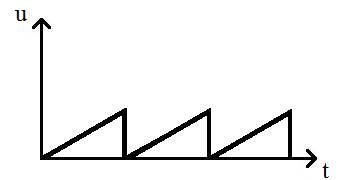
Рис. 72. Пилообразное напряжение
3) Прямоугольные импульсы. Применяются в электронной импульсной технике.
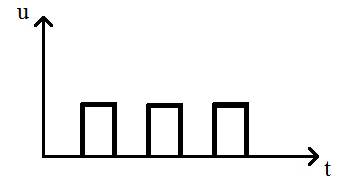
Рис. 73. Прямоугольные импульсы напряжения
Несинусоидальные колебания могут возникать самопроизвольно или генерироваться специальными электронными схемами. Обязательным условием возникновения несинусоидальных колебаний является наличие в схеме нелинейных элементов: диодов, транзисторов, тиристоров и др.
Теорема Фурье
Теорема Фурье утверждает, что любое периодическое несинусоидальное колебание можно разложить на простые составляющие двух типов:
1) одна постоянная составляющая (фактически это постоянный ток или напряжение);
2) несколько синусоидальных составляющих – гармоник.
Совокупность всех составляющих называется рядом Фурье.
Число гармоник в разложении в ряд Фурье зависит от формы несинусоидального колебания. Чем дальше форма несинусоидального колебания от синусоиды – тем больше будет гармоник. Для несинусоидальных колебаний, показанных на рис. 71-73, больше всего гармоник будет в случае колебания в форме прямоугольных импульсов.
Гармоники обозначаются порядковыми номерами: первая, вторая, третья и т.д..
Частота первой гармоники равна частоте несинусоидального колебания. Вторая гармоника имеет вдвое большую частоту, чем первая гармоника, третья – втрое и т.д.
С ростом порядкового номера (порядка) гармоники амплитуда ее, обычно, уменьшается. То есть, вторая гармоника по амплитуде меньше первой, третья меньше второй и т.д. Этот факт позволяет учитывать в расчетах только первые 3 – 5 гармоник. Гармоники с более высокими номерами (высшие) гармоники отбрасываются в силу их небольшой величины. Гармоника с наибольшей амплитудой называется основной.
В разложении несинусоидального колебания в ряд Фурье некоторые составляющие могут отсутствовать. Это зависит от формы исходного колебания. Так, в разложении на гармоники колебания, показанного рис. 74а, отсутствует вторая гармоника, при наличии первой и третьей гармоник.
Пример разложения несинусоидального колебания на составляющие Пример разложения показан на рис. 74. Заметим, что исходная, несинусоидальная кривая имеет "провал" в середине каждого полупериода, а также два "горба". Вся кривая смещена по вертикали относительно горизонтальной оси графика.
Для упрощения здесь специально подобрано колебание, форма которого мало отличается от синусоиды. Поэтому в разложении данной кривой в ряд Фурье будет небольшое число составляющих.
В этом простейшем примере разложения несинусоидального колебания в ряд Фурье содержится только три составляющих: первая гармоника – u1, третья гармоника – u3, а также постоянная составляющая – U0.
Рассмотрим теперь, каким образом сумма составляющих даёт исходное несинусоидальное колебание.
Рассмотрев первый полупериод несинусоидального колебания, можно понять, что "провал" образуется при сложении положительной амплитуды первой гармоники и отрицательной амплитуды третьей гармоники.
“Горбы” образуются от сложения положительных полупериодов первой и третьей гармоник.
Постоянная составляющая сдвигает несинусоидальное колебание выше горизонтальной оси. Она появляется в разложении том случае, если исходное колебание несимметрично относительно горизонтальной оси. Если сложить только гармоники, несинусоидальное напряжение будет симметричным относительно оси времени на графике.
Математическая запись разложения в ряд Фурье выглядит как сумма всех составляющих: постоянной составляющей и гармоник. Для нашего примера несинусоидальное колебание запишется как сумма всех его составляющих:
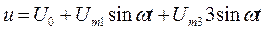
Из записи видно, что частота третьей гармоники втрое выше частоты первой гармоники.
Следует понимать, что каждая составляющая несинусоидального напряжения, приложенного к цепи, стремится вызвать в цепи соответствующую составляющую тока. Другими словами, постоянная составляющая напряжения стремится вызвать в цепи постоянную составляющую тока, первая гармоник напряжения породит первую гармонику тока и т.д. В целом, несинусоидальное напряжение, приложенное к цепи вызовет появление несинусоидального тока в цепи.
Таким образом, математическая запись тока, возникшего в цепи, для нашего примера, может выглядеть так:
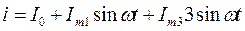
Заметим, что форма колебания для тока в цепи не обязательно будет совпадать с формой напряжения, приложенного к цепи. Это зависит от вида электрической цепи и присутствующих в ней компонентов.
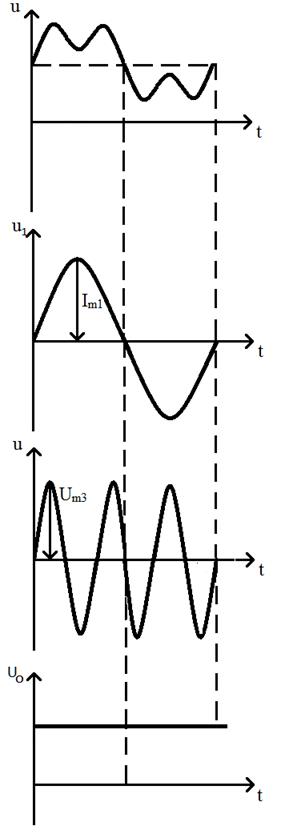
Рис. 74. Разложение несинусоидального колебания в ряд Фурье: а) u – исходное несинусоидальное колебание; б) u1 – первая гармоника,
в) u3 – третья гармоника;
г) Uo – постоянная составляющая.
Пример 16. Расчёт цепи с несинусоидальным напряжением
К цепи, содержащей последовательное соединение элементов: резистора R, индуктивности L, и ёмкости C, подведено несинусоидальное напряжение u = 150 sinωt + 50sin3ωt +30sin5ωt.
Известны сопротивления элементов цепи для частоты первой гармоники: R = 9 Ом, ХL1 = 5 Ом и Xс1 = 45 Ом.
Определить действующие значения несинусоидального напряжения U, тока I и активную мощность Р, выделяющуюся в цепи.
Решение
Математическая запись несинусоидального напряжения, приложенного к цепи содержит три составляющих: первую, третью и пятую гармоники.
Полное сопротивление цепи для первой гармоники
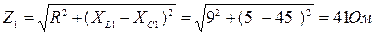
В этой формуле использованы, указанные в условии задачи, сопротивления элементов цепи для первой гармоники.
Аналогично находим полное сопротивление цепи для третьей и для пятой гармоники. Следует учесть, что для третьей гармоники индуктивное сопротивление возрастает втроё, а ёмкостное сопротивление втрое уменьшается по сравнению с сопротивлением для первой гармоники. Соответственно, для пятой гармоники, индуктивное и ёмкостное сопротивления изменятся в пять раз. Активное сопротивление от частоты не зависит.

Амплитудную величину каждой гармоники тока определяем по закону Ома, зная амплитуду напряжения и полное сопротивление цепи для соответствующей гармоники:
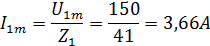
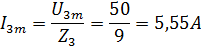
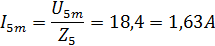
Действующее значение тока в цепи:

Мощность, выделяющаяся в цепи: 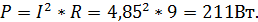
Трехфазный ток
Основные понятия
В промышленности широко используется трехфазный синусоидальный ток. Однофазный ток, применяемый в быту, является частью трехфазной системы.
Значительный вклад в развитие трёхфазных систем внёс наш соотечественник, русский инженер, М. О. Доливо-Добровольский, который впервые предложил связанную (трёх- и четырёхпроводную) систему трёхфазного тока.
Широкое применение трёхфазного тока объясняется достоинствами трехфазной системы:
1) упрощается передача и распределение энергии от электростанции к потребителям;
2) на базе трехфазного тока создан простой, дешевый и надежный электродвигатель; это очень важное достоинство, т.к. для производства любой продукции необходим электродвигатель.
Трехфазной называется система трех одинаковых по амплитуде и частоте синусоидальных величин, смещённых по фазе на 120 градусов относительно друг друга.
Три синусоиды обозначаются буквами A, B и C и, соответственно, называются фазами A, B или С. Эти синусоиды могут изображать напряжение, ток или ЭДС.
График трехфазного напряжения показан на рис. 76. На графике изображены синусоиды трёх напряжений: uА, uB и uC.
По горизонтальной оси графика отложен фазовый угол ωt – угол поворота рамки генератора, в которой индуктируется синусоидальная ЭДС. (Повторите принцип работы и устройство генератора однофазного переменного тока.)
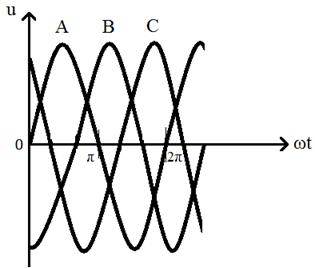
Рис. 76. График трехфазной системы напряжений на волновой диаграмме
Графики трёхфазной системы токов или трехфазной системы ЭДС будут выглядеть аналогично.
Напомним, что каждая синусоида формируется за один полный оборот рамки генератора, который составляет 360 градусов или 2π радиан.
Построение графика трёхфазного тока начинается с построения осей координат, а затем – синусоиды фазы А. Её синусоида начинается из начала координат (в точке 0).
Чтобы удобнее было строить синусоиды фазы B и фазы С, каждый полупериод синусоиды фазы А разбит на три равные части. Полупериод синусоиды соответствует 180 градусам, следовательно в каждом отрезке будет 60 градусов.
После построения синусоиды фазы А строятся две другие синусоиды.
Положительный полупериод синусоиды фазы В начинается на 120 градусов правее начала положительного полупериода синусоиды фазы А. Это означает, что синусоида В отстаёт по фазе от синусоиды фазы А на 120 градусов.
Синусоида фазы С начинается на 120 градусов правее начала положительного полупериода синусоиды фазы В, т.е. отстаёт от синусоиды фазы В на 120 градусов. Можно также сказать, что синусоида фазы С отстаёт по фазе от синусоиды фазы А на 240 градусов.
Математически три синусоиды трёхфазной системы можно записать в виде:
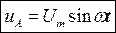
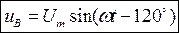

На рис. 77 синусоидальные величины трёхфазной системы показаны на векторной диаграмме
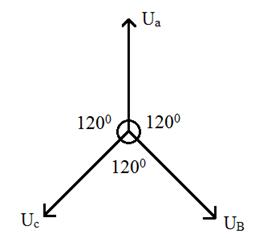
Рис. 77. Изображение трехфазной системы напряжений
на векторной диаграмме
На векторной диаграмме трехфазная система напряжений, токов или ЭДС изображается в виде трех векторов, под углом 120 градусов друг к другу.
Получение трехфазного тока
Генератор трёхфазного тока по принципу работы и конструкции похож на генератор однофазного тока, рассмотренный ранее. Работа генератора основана на явлении электромагнитной индукции. (Повторите принцип работы и устройство генератора однофазного переменного тока.)
В отличие от однофазного генератора, трехфазный имеет не одну, а три рамки, смещенные по окружности на 120 градусов. При вращении рамок в магнитном поле, в каждой из них наводится синусоидальная ЭДС.
В реальном генераторе трехфазного тока используются не три рамки, а три обмотки. Обмотка отличается от рамки тем, что содержит множество витков с целью получить большую величину ЭДС по сравнению с одним витком рамки.
В каждой обмотке трёхфазного генератора индуктируется синусоидальная ЭДС, частотой 50 герц.
Каждая из обмоток имеет два вывода. Выводы обозначаются буквами AX, BY, CZ.
Обмотки генератора, относящиеся к ним провода, а также синусоиды на диаграмме трёхфазной системы, могут быть окрашены в разные цвета.
Фазе А присвоен желтый цвет, фазе В – зелёный и фазе С – красный. При сборке трёхфазных цепей используются провода с изоляцией соответствующих цветов. Разные цвета проводников позволяют легко отличить проводники, относящиеся к одной фазе от проводников других фаз.
Свойства соединения звездой
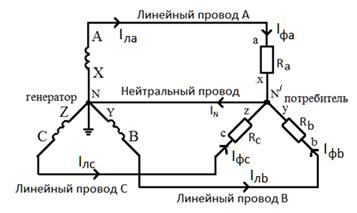
Рис. 79. Соединение обмоток генератора и
сопротивлений потребителя звездой. Нагрузка активная
При соединении звездой генератор и потребитель соединены между собой четырехпроводной линией. Такая линия называется четырёхпроводной. Эти провода называются: линейный провод А, линейный провод В, линейный провод С и нейтральный (нулевой) провод.
Нейтральная точка звезды генератора обозначается буквой N. Она обычно заземлена. Нейтральная точка звезды потребителя обозначается буквой N' (читается: "эн штрих").
Каждая фаза (обмотка) генератора питает одноимённую фазу потребителя. При этом все фазы работают независимо друг от друга. Например, ток в фазе А протекает от начала фазы генератора (точка А), по линейному проводу А, через одноименную фазу потребителя Ra и по нулевому проводу возвращается обратно к концу той же фазы (точка X). Направление протекания тока в фазе А показано на рис. 79. Аналогично протекают токи в фазе B и в фазе С.
Принято считать, что фазные токи в сопротивление потребителя протекают от начала фазы к концу, а линейные - от генератора к потребителю.
Токи, протекающие в трёхфазной схеме имеют названия:
фазным называется ток Iф, протекающий в фазе генератора или потребителя;
линейным – называется ток Iл, протекающий в линейном проводе;
током нейтрали называется ток In, протекающий в нулевом проводе.
В схеме соединения звездой, показанной на рис. 79, можно выделить три линейных и три фазных тока. Как известно, при последовательном соединении элементов электрической цепи, ток одинаков во всех точках цепи. Отсюда следует, что при соединении звездой, в каждой фазе, линейный ток равен фазному току, т.е.
Iла = Iфа, Iлb = Iфb, Iлc = Iфc.
Поскольку в схеме звезда линейный ток равен фазному, индекс л –линейный или ф – фазный, рядом с символом тока I, зачастую не ставится. Остаётся только буква имени фазы: Ia, Ib, или Iс.
В системе звезда можно выделить два вида напряжений (см. рис. 80).
Фазным называется напряжение Uф, измеренное между линейным и нулевым проводом; его можно также измерить между выводами а и х сопротивления фазы потребителя.
Линейным называется напряжение Uл, измеренное между двумя линейными проводами; также можно измерить линейное напряжение между началами двух фаз потребителя – между точками а и с.
В схеме звезда можно измерить три фазных напряжения и три линейных напряжения:
Uфа= Uфb=Uфс=220В; Uл ab=Uл bc=Uл са=380В.
В нашей практике мы работаем с низковольтными трёхфазными сетями, в которых фазное напряжение составляет 220 вольт, а линейное – 380 вольт.
В обозначении фазных и линейных величин буквы "ф" (фазное) и "л" (линейное) часто не указывают. Кроме буквы U остаются только буквы наименования фазы. Например: Uа – напряжение на фазе А; Uac – линейное напряжение между линейными проводами a и с. Заметим, что фазное напряжение обозначается одной буквой нижнего индекса, а линейное – двумя.
Вольтметры, показанные на рис. 80 измеряют: правый – фазное напряжение на фазе А (Uфа); левый – линейное напряжение между линейными проводами А и С (Uл ас).

Рис. 80. Измерение напряжений в системе звезда. Вольтметры измеряют:
линейное напряжение Uac и фазное напряжение Uа
Векторная диаграмма фазных и линейных напряжений имеет вид, показанный на рис. 81.

Рис. 81. Векторная диаграмма линейных и фазных напряжений в системе звезда
На диаграмме хорошо видно, что вектора линейных напряжений длиннее, чем вектора фазных напряжений. Это объясняется тем, что фазное напряжение снимается с одной обмотки трёхфазного генератора, а линейное – является векторной суммой напряжений с двух обмоток. Поэтому линейное напряжение будет больше фазного.
Низковольтную трёхфазную сеть часто называют сетью 220/380 вольт. В этом обозначении первая цифра означает величину фазного напряжения, а вторая – линейного. Низковольтными считаются сети с напряжением до 1000В.
Линейное напряжение в системе звезда больше фазного в корень из трёх раз:
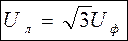
Ток в фазе потребителя, при активной нагрузке, можно найти по закону Ома:

Если нагрузка комплексная, вместо активного сопротивления R следует использовать полное сопротивление Z.
Если все сопротивления в трехфазном потребителе (Ra, Rb и Rc) одинаковы, то такая нагрузка называется равномерной. При равномерной нагрузке все фазные токи одинаковы и все линейные токи одинаковы.
Рассмотрев протекание токов во всех фазах, нетрудно заметить, что в нейтральном (нулевом) проводе протекают токи всех трёх фаз. Следовательно:
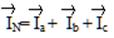
Однако, не следует думать, что ток в нулевом проводе можно найти, сложив арифметически три фазных тока. Такое действие будет грубой ошибкой.
Ток нейтрали действительно равен сумме трёх фазных токов, только сумма эта векторная, а не арифметическая. Вектора фазных токов нужно суммировать путём выполнения графических построений. Найти ток нейтрали, при известных фазных токах, можно путем построения в масштабе векторной диаграммы. Далее рассмотрен способ нахождения тока нейтрали (пример 17).
Векторная диаграмма для токов строится аналогично диаграмме для напряжений в системе звезда. Три фазные тока будут направлены под углом 120 градусов друг к другу. Данную диаграмму мы строим применительно к схеме показанной на рис. 80 для случая активной нагрузки. При активной нагрузке ток совпадает по фазе с напряжением, приложенным к сопротивлению фазы. Поэтому каждый из фазных токов направлен также, как соответствующее фазное напряжение.
Интересно, что при равномерной нагрузке ток нейтрали равен нулю. Причина этого становится понятной из рассмотрения векторной диаграммы, показанной на рис. 82.
Чтобы построить на векторной диаграмме ток нейтрали нужно сложить вектора трёх фазных токов: Ia, Ib и Ic. Для упрощения проведём сложение векторов в три этапа Сначала, по правилу параллелограмма суммируем вектор Ib с вектором Ic. Получится суммарный вектор Ic+Ib. Видно, что это вектор равен по длине вектору Ia и направлен противоположно к нему. Следовательно сумма этих двух векторов будет равна нулю.
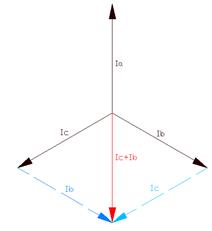
Рис. 82. Векторная диаграмма токов в системе звезда при равномерной нагрузке
Получается, что ток в нулевом проводе, при равномерной нагрузке, равен нулю. Но, если в нулевом проводе не протекает ток, нулевой провод можно убрать и система будет прекрасно работать без него! Это действительно так. В случае равномерной нагрузки без нулевого провода можно обойтись. Однако, на практике нулевой провод прокладывают всегда. Это объясняется тем, что в случае аварии равномерная нагрузка может стать неравномерной, а она не сможет нормально работать без нулевого провода.
Пример 17. Расчёт соединения звездой
Звездой соединены три лампы накаливания. В фазе А включена лампа, мощностью 60 вт, в фазе В – лампа мощностью 100 Вт и в фазе С – лампа мощностью 100 Вт. Трёхфазная сеть стандартная: 220/380 вольт.
Найти ток в каждой фазе, сопротивление каждой лампы и ток, протекающий в нейтральном проводе (ток нейтрали).
Решение
Схема включения ламп показана на рис. 84.

Рис. 84. Схема к примеру 17. Три лампы накаливания соединены звездой
Из условия задачи и свойств соединения звездой ясно, что на каждую лампу подаётся фазное напряжение 220 вольт. Лампы неодинаковы, следовательно, нагрузка неравномерная.
Зная мощность лампы и напряжение на ней, найдём ток, протекающий через лампу. Мощность, при активной нагрузке, вычисляется по формуле P= U*I, следовательно токи в фазах (в каждой из ламп) составят:
Ia= Pa/Uа = 60/220 = 0,27А;
Ib= P/Ub = 100/220 = 0,45А;
Ic= Pc/Uc = 100/220 = 0,45А.
Сопротивление каждой лампы найдем по закону Ома:
Ra = Ua / Ia =220/0,27 = 815 Ом;
Rb = Ub / Ib =220/0,45= 489 Ом;
Rc = Uc / Ic =220/0,45 = 489 Ом.
Пример 18. Расчёт мощности потребителя при соединении звездой
По данным примера 17 определить мощность, потребляемую всеми тремя лампами
Решение:
В любой электрической схеме, в том числе в трехфазной системе, общая мощность равна сумме мощностей, потребляемых элементами схемы. Поскольку мощность каждой из ламп известна, общая мощность трёхфазной системы
Pобщ = Pa+Pb+Pc = 60+100+100 = 360Вт.
Пример 19. Расчёт тока, потребляемого трёхфазным электродвигателем, по его параметрам
Трёхфазный электродвигатель, обмотки которого соединены звездой, подключён к стандартной трёхфазной сети с линейным напряжением Uл =380 В. Частота тока в сети - 50 Гц.
Известны паспортные данные двигателя: механическая мощность двигателя 4,2 КВт, КПД=h=0,72 (72%), коэффициент мощности – cosj =0,85.
Определить: а) фазные токи, потребляемые двигателем; б) параметры обмотки двигателя.
Решение.
А) Найдем ток, потребляемый каждой обмоткой двигателя.
На статоре трёхфазного двигателя уложено три обмотки. Каждая обмотка представляет собой реальную катушку индуктивности и изображена на схеме в виде цепочки RL, т.е. как последовательное соединение активного сопротивления и индуктивности.
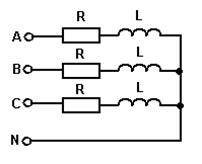
Рис. 86. Схема включения обмоток двигателя к примеру 19.
В паспортных данных двигателя указана механическая мощность P2 (мощность на валу двигателя). Для расчёта электрических параметров двигателя необходимо знать электрическую мощность P1, потребляемую двигателем от трёхфазной питающей сети.
Механическая (полезная) мощность P2 всегда меньше, чем электрическая мощность P1, потребляемая от сети. По формуле КПД найдем электрическую мощность, потребляемую двигателем.
КПД=h= Pмех/Pэл=P2/P1, откуда:
Рэл = Рмех /h =4200 / 0,72 = 5833 Вт.
По формуле мощности трёхфазной системы найдём ток, потребляемый одной фазой двигателя:
Iф = Iл = Рэл / 3Uф сosj = 5833 / 3 * 220 * 0,85 = 10,4 А.
Фазное напряжение Uф, необходимое для расчёта найдено, зная соотношение между линейным и фазным напряжением, по формуле:
Uф = Uл /  =220 В.
=220 В.
Б) Находим параметры обмотки двигателя: её активное сопротивление и индуктивность.
Полное сопротивление фазы двигателя, т.е. полное сопротивление такой катушки можно найти из закона Ома для реальной катушки, зная напряжение на фазе и ток фазы:
Zф = Uф / Iф =220 / 10,4 = 21,15 Ом.
Зная соотношения для реальной катушки индуктивности, найдём активную и реактивную составляющие полного сопротивления фазы двигателя:
Rф = Zф * cosj =21,15 * 0,85 = 18 Ом.
XL = 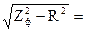
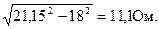
Из формулы индуктивного сопротивления катушки найдём индуктивность фазы двигателя:
L = XL / 2pf = 11,1 / 2*3.14*50 = 0,035 Гн.
Пример 20. Расчет потребителя при соединении в треугольник
Три одинаковых лампы накаливания включены треугольником. Сопротивление каждой лампы 484 Ом. Вольтметр показывает напряжение 220 вольт. Определить фазные и линейные токи в схеме. Найти мощность, потребляемую всей схемой.
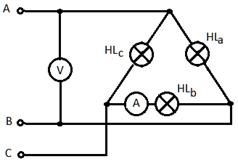
Рис. 88. Схема к примеру 20.
Соединение ламп накаливания в треугольник
Решение
Вольтметр подключён между линейными проводами и показывает линейное напряжение. Оно в треугольнике равно фазному и равно 220В.
Сопротивление каждой фазы потребителя Rф равно сопротивлению лампы Rл. Фазные токи можно найти по закону Ома:
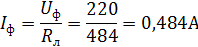
Линейный ток в каждой фазе найдём по формуле:
Iл=  Iф=1,73*0,484=1,15А.
Iф=1,73*0,484=1,15А.
Общая мощность, потребляемая схемой, равна утроенной мощности одной фазы, т.к. нагрузка равномерная:
Pоб=3Pф=3*100=300вт.
Оглавление
Несинусоидальные колебания
Основные понятия...............................................................................................................с. 4
Теорема Фурье.....................................................................................................................с. 5
Пример разложения несинусоидального колебания на составляющие.........................с. 6
Способы разложения несинусоидального колебания в ряд Фурье................................с. 7
Действующее значение несинусоидального колебания
Мощность, выделяющаяся несинусоидальным колебанием..........................................с. 9
Расчет цепей с несинусоидальными колебаниями..........................................................с. 9
Пример 16. Расчёт цепи с несинусоидальным напряжением....................................с. 10
Трехфазный ток
Основные понятия..............................................................................................................с. 11
Получение трехфазного тока............................................................................................с. 13
Способы соединения обмоток трёхфазного устройства................................................с. 13
Свойства соединения звездой...........................................................................................с. 14
Связь между трёхфазной и однофазной сетью...............................................................с. 18
Пример 17. Расчёт соединения звездой......................................................................с. 19
Построение векторной диаграммы для соединения звездой.........................................с. 20
Мощность в трёхфазной системе.....................................................................................с. 21
Пример 18. Расчёт мощности потребителя при соединении звездой......................с. 21
Пример 19. Расчёт тока, потребляемого трёхфазным электродвигателем, по его параметрам..............................................................................................с. 22
Свойства соединения треугольником...............................................................................с. 23
Пример 20. Расчет потребителя при соединении в треугольник..............................с. 24
МИНИСТЕРСТВО КУЛЬТУРЫ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего и послевузовского профессионального образования
ВСЕРОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ КИНЕМАТОГРАФИИ имени С.А. ГЕРАСИМОВА
СЕРГИЕВО-ПОСАДСКИЙ ФИЛИАЛ
КОНСПЕКТ ЛЕКЦИЙ
ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
Часть 3
Несинусоидальные колебания.
Трёхфазный ток
для специальности среднего профессионального образования
070208
«Театральная и аудиовизуальная техника (по видам)»
(углублённая подготовка)
Сергиев Посад
2015
Рассмотрено на заседании Утверждаю:
предметной комиссии заместитель директора по УР
протокол № от Л.Г. Зуденкова
председатель ПК
М. П. Лебедь
Разработал преподаватель М.П. Лебедь
Рецензент: преподаватель Н.Л. Новинский
Вступление
Третья часть является продолжением первой и второй частей конспекта лекций по курсу "Основы электротехники" и включает в себя материал по разделам "Несинусоидальные колебания" и "Трёхфазный ток".
В работу включён минимально необходимый для сдачи экзамена объём материала. Теоретический материал иллюстрирован примерами решения задач.
Нумерация рисунков и примеров решения задач в тексте продолжает нумерацию предыдущих частей.

конспекта лекций по курсу основы электротехники
Несинусоидальные колебания
Основные понятия
В электротехнике и в электронике широко применяются колебания, форма которых отличается от синусоиды. Любое такое колебание относится к несинусоидальным.
Рассмотрим некоторые, часто встречающиеся формы несинусоидальных колебаний:
1) Пульсирующее напряжение. Встречается в выпрямителях, преобразующих синусоидальное напряжение в постоянное.

Рис. 71. Пульсирующее напряжение
В отличие от синусоидального колебания, пульсирующее изменяется только по величине, но не изменяется по направлению. Пульсирующее напряжение не меняет своей полярности, а синусоидальное меняет полярность при смене полупериода.
2) Пилообразное колебание. Используется при формирования изображения в электронно-лучевых трубках.

Рис. 72. Пилообразное напряжение
3) Прямоугольные импульсы. Применяются в электронной импульсной технике.
Рис. 73. Прямоугольные импульсы напряжения
Несинусоидальные колебания могут возникать самопроизвольно или генерироваться специальными электронными схемами. Обязательным условием возникновения несинусоидальных колебаний является наличие в схеме нелинейных элементов: диодов, транзисторов, тиристоров и др.
Теорема Фурье
Теорема Фурье утверждает, что любое периодическое несинусоидальное колебание можно разложить на простые составляющие двух типов:
1) одна постоянная составляющая (фактически это постоянный ток или напряжение);
2) несколько синусоидальных составляющих – гармоник.
Совокупность всех составляющих называется рядом Фурье.
Число гармоник в разложении в ряд Фурье зависит от формы несинусоидального колебания. Чем дальше форма несинусоидального колебания от синусоиды – тем больше будет гармоник. Для несинусоидальных колебаний, показанных на рис. 71-73, больше всего гармоник будет в случае колебания в форме прямоугольных импульсов.
Гармоники обозначаются порядковыми номерами: первая, вторая, третья и т.д..
Частота первой гармоники равна частоте несинусоидального колебания. Вторая гармоника имеет вдвое большую частоту, чем первая гармоника, третья – втрое и т.д.
С ростом порядкового номера (порядка) гармоники амплитуда ее, обычно, уменьшается. То есть, вторая гармоника по амплитуде меньше первой, третья меньше второй и т.д. Этот факт позволяет учитывать в расчетах только первые 3 – 5 гармоник. Гармоники с более высокими номерами (высшие) гармоники отбрасываются в силу их небольшой величины. Гармоника с наибольшей амплитудой называется основной.
В разложении несинусоидального колебания в ряд Фурье некоторые составляющие могут отсутствовать. Это зависит от формы исходного колебания. Так, в разложении на гармоники колебания, показанного рис. 74а, отсутствует вторая гармоника, при наличии первой и третьей гармоник.
Пример разложения несинусоидального колебания на составляющие Пример разложения показан на рис. 74. Заметим, что исходная, несинусоидальная кривая имеет "провал" в середине каждого полупериода, а также два "горба". Вся кривая смещена по вертикали относительно горизонтальной оси графика.
Для упрощения здесь специально подобрано колебание, форма которого мало отличается от синусоиды. Поэтому в разложении данной кривой в ряд Фурье будет небольшое число составляющих.
В этом простейшем примере разложения несинусоидального колебания в ряд Фурье содержится только три составляющих: первая гармоника – u1, третья гармоника – u3, а также постоянная составляющая – U0.
Рассмотрим теперь, каким образом сумма составляющих даёт исходное несинусоидальное колебание.
Рассмотрев первый полупериод несинусоидального колебания, можно понять, что "провал" образуется при сложении положительной амплитуды первой гармоники и отрицательной амплитуды третьей гармоники.
“Горбы” образуются от сложения положительных полупериодов первой и третьей гармоник.
Постоянная составляющая сдвигает несинусоидальное колебание выше горизонтальной оси. Она появляется в разложении том случае, если исходное колебание несимметрично относительно горизонтальной оси. Если сложить только гармоники, несинусоидальное напряжение будет симметричным относительно оси времени на графике.
Математическая запись разложения в ряд Фурье выглядит как сумма всех составляющих: постоянной составляющей и гармоник. Для нашего примера несинусоидальное колебание запишется как сумма всех его составляющих:
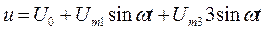
Из записи видно, что частота третьей гармоники втрое выше частоты первой гармоники.
Следует понимать, что каждая составляющая несинусоидального напряжения, приложенного к цепи, стремится вызвать в цепи соответствующую составляющую тока. Другими словами, постоянная составляющая напряжения стремится вызвать в цепи постоянную составляющую тока, первая гармоник напряжения породит первую гармонику тока и т.д. В целом, несинусоидальное напряжение, приложенное к цепи вызовет появление несинусоидального тока в цепи.
Таким образом, математическая запись тока, возникшего в цепи, для нашего примера, может выглядеть так:
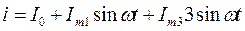
Заметим, что форма колебания для тока в цепи не обязательно будет совпадать с формой напряжения, приложенного к цепи. Это зависит от вида электрической цепи и присутствующих в ней компонентов.

Рис. 74. Разложение несинусоидального колебания в ряд Фурье: а) u – исходное несинусоидальное колебание; б) u1 – первая гармоника,
в) u3 – третья гармоника;
г) Uo – постоянная составляющая.
Способы разложения несинусоидального колебания в ряд Фурье
Разложение периодического несинусоидального колебания в ряд Фурье можно выполнить несколькими способами.
1-й способ
В справочнике по высшей математике рассмотрены часто встречающихся несинусоидальных кривые и записаны формулы для составляющих ряда Фурье.
2-й способ
Можно воспользоваться математическими формулами и самостоятельно разложить несинусоидальное колебание на составляющие.
3-й способ
Можно определить параметры составляющих несинусоидального колебания с помощью специального прибора, который называется "анализатор спектра". Этот способ наиболее пригоден для практики.
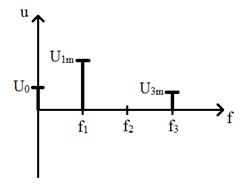
Рис. 75. Спектральный состав несинусоидального колебания,
изображенного на рис. 74
Под термином “спектр несинусоидального колебания" подразумевают совокупность составляющих, входящие в ряд Фурье. Термин "спектр" используется по аналогии с разложением белого света на 7 цветов радуги с помощью стеклянной призмы.
Анализатор спектра позволяет по отдельности измерить амплитуду и частоту каждой гармоники.
После измерения параметров каждой составляющей, можно построить график спектрального состава несинусоидального колебания:
по вертикальной оси откладывается амплитуда каждой составляющей, а по горизонтальной – ее частота.
Спектр наглядно показывает, какие составляющие содержатся в разложении несинусоидального колебания и какова величина каждой составляющей (рис. 75).
Дата: 2019-07-24, просмотров: 532.