Вариант 1
1. Вычислите: 1) 15 327+ 496 383; 2) 38 020 405 – 9 497 653.
2. На одной стоянке было 143 автомобиля, что на 17 автомобилей больше, чем на второй. Сколько автомобилей было на обеих стоянках?
3. Выполните сложение, выбирая удобный порядок вычислений:
1) (325 + 791) + 675; 2) 428 + 856 + 572 + 244.
4. Проверьте, верно ли неравенство:
1 674 – (736 + 328)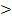 
2 000 – (1 835 – 459).
5. Найдите значение 𝑎 по формуле 𝑎 = 4𝑏 – 16 при 𝑏 = 8.
6. Упростите выражение 126 + 𝒙 + 474 и найдите его значение при 𝒙 = 278.
7. Вычислите:
1) 4 м 73 см + 3 м 47 см; 2) 12 ч 16 мин – 7 ч 32 мин.
8. Найдите значение выражения, выбирая удобный порядок вычислений:
1) (713 + 529) – 413; 2) 624 – (137 + 224).
Вариант 2
1. Вычислите: 1) 17 824+ 128 356; 2) 42 060 503 – 7 456 182.
2. На одной улице 152 дома, что на 18 домов меньше, чем на другой. Сколько всего домов на обеих улицах?
3. Выполните сложение, выбирая удобный порядок вычислений:
1) (624 + 571) + 376; 2) 212 + 497 + 788 + 803.
4. Проверьте, верно ли неравенство:
1 826 – (923 + 249) 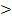3 000 – (2 542 – 207).
5. Найдите значение 𝑝 по формуле 𝑝= 40 – 7𝑞 при 𝑞 = 4.
6. Упростите выражение 235 + y + 465 и найдите его значение при y = 153.
7. Вычислите:
1) 6 м 23 см + 5 м 87 см; 2) 14 ч 17 мин – 5 ч 23 мин.
8. Найдите значение выражения, выбирая удобный порядок вычислений:
1) (837 + 641) – 537; 2) 923 – (215 + 623).
Вариант 3
1. Вычислите: 1) 26 832 + 573 468; 2) 54 073 507 – 6 829 412.
2. В одном классе 37 учащихся, что на 9 человек больше, чем во втором. Сколько всего учащихся в обоих классах?
3. Выполните сложение, выбирая удобный порядок вычислений:
1) (736 + 821) + 264; 2) 573 + 381 + 919 + 627.
4. Проверьте, верно ли неравенство:
2 491 – (543 + 1 689)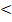 
1 000 – (931 – 186).
5. Найдите значение 𝑦 по формуле 𝑦 = 3𝑥 + 18 при 𝑥 = 5.
6. Упростите выражение 433 + 𝑎 + 267 и найдите его значение при 𝑎 = 249.
7. Вычислите:
1) 7 м 23 см + 4 м 81 см; 2) 6 ч 38 мин – 4 ч 43 мин.
8. Найдите значение выражения, выбирая удобный порядок вычислений:
1) (674 + 245) – 374; 2) 586 – (217 + 186).
Вариант 4
1. Вычислите: 1) 19 829 + 123 471; 2) 61 030 504 – 8 695 371.
2. На одной книжной полке стоят 23 книги, что на 5 книг меньше, чем на другой. Сколько всего книг стоит на обеих полках?
3. Выполните сложение, выбирая удобный порядок вычислений:
1) (349 + 856) + 651; 2) 166 + 452 + 834 + 748.
4. Проверьте, верно ли неравенство:
1 583 – (742 + 554) 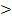1 000 – (883 – 72).
5. Найдите значение 𝑥 по формуле 𝑥 = 16 + 8𝑧 при 𝑧 = 7.
6. Упростите выражение 561 + 𝑏 + 139 и найдите его значение при 𝑏 = 165.
7. Вычислите:
1) 9 м 41 см + 4 м 72 см; 2) 18 ч 18 мин – 5 ч 24 мин.
8. Найдите значение выражения, выбирая удобный порядок вычислений:
1) (563 + 721) – 363; 2) 982 – (316 + 582).
Контрольная работа № 3
Уравнение. Угол. Многоугольники.
Вариант 1
1. Постройте угол МКА, величина которого равна 74 
. Проведите произвольно луч КС между сторонами угла МКА. Запишите образовавшиеся углы и измерьте их величины.
2. Решите уравнение: 1) 𝑥 +37 = 81 2) 150 – 𝑥 = 98.
3. Одна из сторон треугольника равна 24 см, вторая – в 4 раза короче первой, а третья – на 16 см длиннее второй. Вычислите периметр треугольника.
4. Решите уравнение: 1) (34 + 𝑥) – 83 = 42 2) 45 – (𝑥 – 16) = 28.
5. Из вершины развёрнутого угла АВС (см рис.) проведены два луча ВD и ВЕ так, что ∠АВЕ = 154 , ∠DВС = 128 . Вычислите градусную меру угла DВЕ.
6. Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
52 – (𝑎 – 𝑥) = 24 было число 40?
Вариант 2
1. Постройте угол ABC, величина которого равна 168 . Проведите произвольно луч BM между сторонами угла ABC. Запишите образовавшиеся углы и измерьте их величины.
2. Решите уравнение: 1) 21 + 𝑥 = 58 2) 𝑥 – 135 = 76.
3. Одна из сторон треугольника равна 32 см, вторая – в 2 раза короче первой, а третья – на 6 см короче первой. Вычислите периметр треугольника.
4. Решите уравнение: 1) (96 – 𝑥) – 15 = 64 2) 31 – (𝑥 + 11) = 18.
5. Из вершины прямого угла MNK (см рис.) проведены два луча ND и NE так, что ∠MND = 73 , ∠KNF = 48 . Вычислите градусную меру угла DNF.
6. Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
64 – (𝑎 – 𝑥) = 17 было число 16?
Вариант 3
1. Постройте угол FDK, величина которого равна 56 . Проведите произвольно луч DT между сторонами угла FDK. Запишите образовавшиеся углы и измерьте их величины.
2. Решите уравнение: 1) 𝑥 + 42 = 94 2) 284 – 𝑥 = 121.
3. Одна из сторон треугольника равна 12 см, вторая – в 3 раза длиннее первой, а третья – на 8 см короче второй. Вычислите периметр треугольника.
4. Решите уравнение: 1) (41 + 𝑥) – 12 = 83 2) 62 – (𝑥 – 17) = 31.
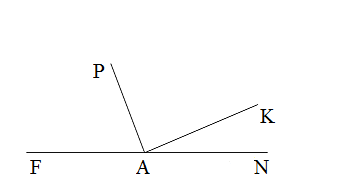
5. Из вершины развёрнутого угла FAN (см рис.) проведены два луча AK и AP так, что ∠NAP = 110 , ∠FAK = 132 . Вычислите градусную меру угла PAK.
6. Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
(69 – 𝑎) – 𝑥 = 23 было число 12?
Вариант 4
1. Постройте угол NMC, величина которого равна 58 . Проведите произвольно луч MB между сторонами угла NMC. Запишите образовавшиеся углы и измерьте их величины.
2. Решите уравнение: 1) 𝑥 + 53 = 97 2) 142 – 𝑥 = 76.
3. Одна из сторон треугольника равна 30 см, вторая – в 5 раза короче первой, а третья – на 22 см длиннее второй. Вычислите периметр треугольника.
4. Решите уравнение: 1) (58 + 𝑥) – 23 = 96 2) 54 – (𝑥 – 19) = 35.
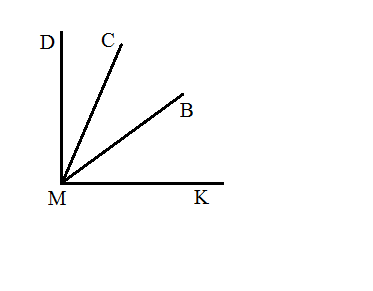
5. Из вершины прямого угла DMK (см рис.) проведены два луча MB и MC так, что ∠DMB = 51 , ∠KMC = 65 . Вычислите градусную меру угла BMC.
6. Какое число надо подставить вместо 𝑎, чтобы корнем уравнения
(𝑎 – 𝑥) – 14 = 56 было число 5?
Контрольная работа № 4
Дата: 2019-07-24, просмотров: 280.
