Магнитное поле и его характеристики.
Магнитное поле – силовое поле, которое существует вокруг постоянных магнитов и проводников с током.
Магнитное поле, в отличие от электростатического, действует только на движущиеся электрические заряды и постоянные магниты (магнитная стрелка).
Для того чтобы обнаружить магнитное поле используется пробная рамка или магнитная стрелка.
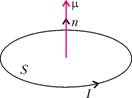Pm=IS – магнитный момент
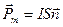
При внесении такой рамки в магнитное поле на неё начинает действовать вращательный момент:
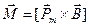
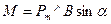Рамка неподвижна при α=0
Mmax=PmB (α=П/2)
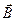- векторная силовая характеристика магнитного поля, вектор В всегда направлен по касательной к силовой линии магнитного поля.
Силовые линии магнитного поля – это замкнутые кривые, в отличие от электростатического поля.
Кроме вектора В для описания магнитного поля в воздухе и вакууме используется характеристика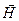 
- напряженность магнитного поля [А/м].
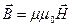; μ – магнитная проницаемость среды, μ0 – магн. Постоянная = 4п·10-7 Н/А2
μ=1 в вакууме.
Проведём аналогию с электростатическим полем:
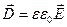; Е зависит от ε.
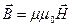; В зависит от μ.
Следовательно В и Е зависят от свойств среды, а D и Н не зависят.
Закон Био-Савара-Лапласа и его применение.
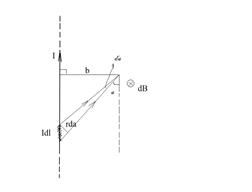
Рассмотрим проводник произвольной формы. Выбираем бесконечно малый участок dl. Точка в пространстве соединена с dl вектором r.
Закон Био-Савара-Лапласа позволяет рассчитать элементарную индукцию dB в произвольной точке пространства.
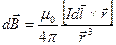
В скалярном виде:
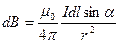
Закон: элементарная индукция прямопропорциональна величине тока, синусу угла между Idl и r и обратнопропорциональна квадрату расстояния от элементарного тока до данной точки.
Для расчета индукции поля используется принцип суперпозиции:
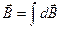; находится как векторная сумма (интеграл) элементарных индукций dB. Интегрирование производится по всей длине проводника.
1) Магнитное поле, созданное прямым проводником с током бесконечной длины.
b<<l, тогда мы можем рассматривать проводник как бесконечный.
Т.к. все dB направлены одинаково, мы можем воспользоваться принципом суперпозиции в скалярном виде.
Выразим все переменные через угол альфа:
; 
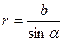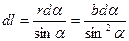
Тогда:
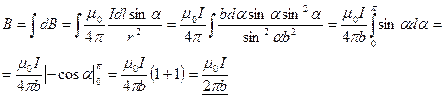2) Проводник конечной длины.
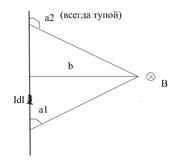
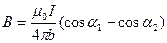
3) Индукция в центре кругового тока.
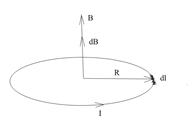
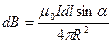
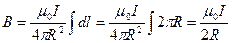
4) Индукция на расстоянии х от центра кругового тока.
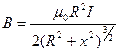
Закон Ампера.
Сила Ампера – это сила, кот. действует на проводник с током в магнитном поле.
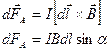
Если поле однородно, то В=const и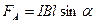 
.
Направление сила Ампера определяется по правилу векторного произведения (левой руки).
Рассмотрим силу, которая действует на элементарный ток I2dl, который находится в магнитном поле, созданным другим бесконечным проводником с током I1.
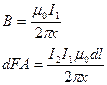
Т Гаусса для вектора В.
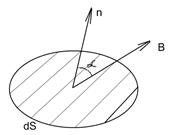Рассмотрим в магнитном поле. бесконечно малую площадку dS, расположенную под углом α.
Тогда бесконечно малый магнитный поток:
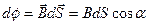
Для того, чтобы найти маг поток через поверхность площадью S необходимо просуммировать:
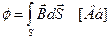
Если поле однородно, то Ф=BScosα
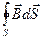- поток вектора В через произвольную замкнутую поверхность.
Т Гаусса: Поток вектора В через произвольную замкнутую поверхность равен 0.
Сравним с электростатическим полем:
;
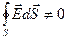В электростатическом поле силовые линии не замкнуты (начинаются на +, заканчиваются на – или в ∞), а силовые линии магнитного поля – замкнутые кривые.
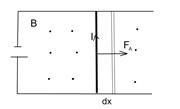7. Работа по перемещению проводника с током в магнитном поле.
Рассмотрим контур с током с подвижной перемычкой.
За бесконечно малый промежуток времени под действием силы ампера перемычка переместится на dx.
При этом будет совершена работа:
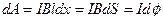
При В=const очевидно, что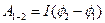 
Если неоднородно: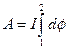 
Билет 28. Квантовая природа излучения. Формула Планка.
На рубеже веков Планк выдвинул квантовую гипотезу о том, что атомные асциляторы излучают не непрерывно, а прерывно и порция этого излучения hʋ=hc/λ=Wф (фотон) квант излучения h=6,6*10-34 Дж*с - постоянная Планка
Эта гипотеза позволила Планку получить формулу, которая полностью описала экспериментальную зависимость U(λ,T)
U(λ,T)=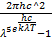 
Формула Планка
Она дала возможность теоретически рассчитывать излучательную способность а.ч.т. для разных длин волн и температур.
Эффект Комптона.
Комптон исследовал рассеяние монохроматических рентгеновских лучей веществом с легкими атомами (например В, парафин) у этих атомов e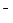 
слабо связаны с ядром. При падении рент. лучей с длинной волны λ на такие атомы, было обнаружено рассеянное рент. излучение с λ > чем λ падающего излучения.
На основе анализа многочисленных экспериментальных данных Комптон вывел формулу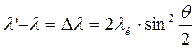 
, где θ – угол рассеяния, 
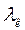– постоянная Комптона 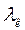= 0,0243Å (анкстрем 
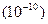м)
Однако эл-маг. теория не смогла объяснить эффект Комптона.
Исходя из квантовых представлений о природе рентгеновского излучения этот эффект удалось объяснить следующим образом: РИС.
В эффекте Комптона кроме рассеянного фотона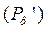 
из атома выбивается e 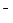отдачи и импульс этого электрона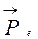 
Закон сохранения импульсов:
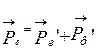
Закон сохранения энергии:
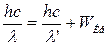, где λ – дл. волны падающего λ’ – рассеивающего
При совместном решении 1-ого и 2-ого уравнения было теоретически рассчитано комптоновское смещени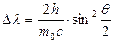е 
, где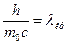 
Такое совпадение еще раз подтвердило правильность представлений о коротковолновом рентгеновском излучении, как о потоке фотонов, обладающих импульсом и энергией.
Магнитное поле и его характеристики.
Магнитное поле – силовое поле, которое существует вокруг постоянных магнитов и проводников с током.
Магнитное поле, в отличие от электростатического, действует только на движущиеся электрические заряды и постоянные магниты (магнитная стрелка).
Для того чтобы обнаружить магнитное поле используется пробная рамка или магнитная стрелка.
Pm=IS – магнитный момент
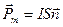
При внесении такой рамки в магнитное поле на неё начинает действовать вращательный момент:
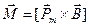
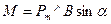Рамка неподвижна при α=0
Mmax=PmB (α=П/2)
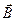- векторная силовая характеристика магнитного поля, вектор В всегда направлен по касательной к силовой линии магнитного поля.
Силовые линии магнитного поля – это замкнутые кривые, в отличие от электростатического поля.
Кроме вектора В для описания магнитного поля в воздухе и вакууме используется характеристика 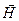- напряженность магнитного поля [А/м].
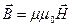; μ – магнитная проницаемость среды, μ0 – магн. Постоянная = 4п·10-7 Н/А2
μ=1 в вакууме.
Проведём аналогию с электростатическим полем:
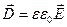; Е зависит от ε.
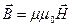; В зависит от μ.
Следовательно В и Е зависят от свойств среды, а D и Н не зависят.
Дата: 2019-07-24, просмотров: 183.
