Синусоидально изменяющиеся величины характеризуются следующими основными параметрами:

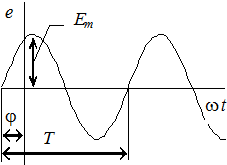
− период Т, [c] - время совершения одного полного колебания синусоидальной величины;

− частота f, [c^-1]=[Гц] - количество периодов, укладывающихся в единицу времени:

.

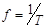В нашей стране частота тока в сети f=50 Гц (достигается вращением роторов в генераторах с частотой вращения n _вр =3000 мин^-1 (об/мин);

− угловая (циклическая) частота изменения тока:

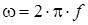, рад/c. Для нашей сети w=314 рад/c;

− амплитуда I_m, E_m, U_m - наибольшее значение синусоидальной величины. Амплитудные значения синусоидальных функций являются постоянными величинами, т.е. от времени они не зависят.

− мгновенные значения синусоидальных функций обозначают маленькими буквами: i, e, u. Они являются функциями времени. Зависимость их от времени выражается соотношениями:

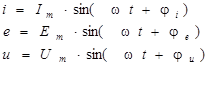
− фаза - аргумент синусоидальной функции (wt+j) - показывает, какое значение имеет синусоидальная функция в данный момент времени;

− начальная фаза j - показывает, какое значение имеет синусоидальная функция в момент начала отсчета, т.е. при t=0;

Действующее значение переменного тока

Действующим значением I переменного тока называют такое значение постоянного I, который, протекая по сопротивлению R, за время, равное одному периоду Т изменения тока, выделяет в нем такое же количество теплоты Q, что и переменный ток i. Поясним определение на примере:

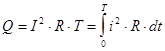, где .

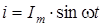После подстановки значения тока i и последующих преобразований получим, что действующее значение переменного тока равно:

.

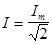Аналогичные соотношения могут быть получены также для напряжения и ЭДС:

        .

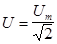
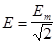Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.

Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за половину периода:

Представления синусоидальных ЭДС, напряжений и токов виде вращающихся векторов и в виде комплексных величин. Комплексные амплитуды синусоидальных ЭДС, напряжения и тока. Оператор поворота комплексной амплитуды и соответствующая векторная диаграмма.

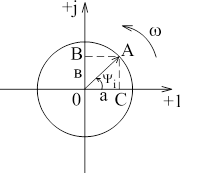(Нарисовать 3 таких рисунка, над векторами подписать I, U, R на разных рисунках).

Длина отрезка ОА в принятом масштабе равна амплитуде тока (ЭДС, напряжения). Проекция вектора на ось ординат (ОВ) равна мгновенному значению тока (ЭДС, напряжение) в момент времени. При вращении вектора в положительном направлении (т.е. против часовой стрелки) с угловой скоростью в любой момент времени его проекция на ось ординат будет равна соответствующему мгновенному значению тока (ЭДС, напряжение):

i=I_msin(ωt+φ_i) (e=E_msin(ωt+φ_i); u=U_msin(ωt+φ_i))

Любой вектор на плоскости, проведенный из начала координат и изображающий значение ЭДС, напряжения или тока, однозначно определяется точкой, соответствующей концу этого вектора (т. А).

Комплексное число (соответствующее точке ) имеет вещественную (ОС) и мнимую (ОВ) составляющие на комплексной плоскости.

Соответственно формулы для тока, ЭДС и напряжения будут выглядеть так:

I_m= I_me^j𝜓= I_mcos𝜓_i+ jI_msin𝜓_i

E_m= E_me^j𝜓= E_mcos𝜓_i+ jE_msin𝜓_i

U_m= U_me^j𝜓= U_mcos𝜓_i+ jU_msin𝜓_i

j- оператор поворота комплексной амплитуды