1) Если известно направление двух точек плоской фигуры, то мгновенный центр скоростей лежит в точке пересечения перпендикуляров к этим скоростям, отложенных в самих точках
| А |
| U̅B |
| U̅А |
| B |
| M |
| M – Мгновенный центр скоростей |
2) Если скорости точек А и В плоской фигуры параллельны между собой и перпендикулярны АВ и модули U̅A и U̅B известны, то мгновенный центр скоростей лежит на пересечении прямой соединяющей концы векторов скоростей и прямой АВ.
| А |
| B |
| M |
| U̅B |
| U̅A |
| M – Мгновенный центр скоростей |
Если U̅A и U̅B равны и сонаправлены, то мгновенный центр скоростей лежит в бесконечности. Угловая скорость при этом будет равна 0
3) Если скорости точек А и В плоской фигуры параллельны между собой и не перпендикулярны АВ, то мгновенный центр скоростей лежит в бесконечности.
4) Если тело катится без скольжения по некоторой неподвижной поверхности, то мгновенный центр скоростей лежит в точке соприкосновения поверхности и тела.
| M |
| M – Мгновенный центр скоростей |
9. Распределение ускорений точек тела при плоском движении. Формула сложения ускорений.
Ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки в ее вращении вместе с плоской фигурой вокруг полюса.
a̅A = a̅O + a̅OA;
a̅OA = a̅OAτ + a̅OAn
10. Аналитический и геометрический способы нахождения ускорений точек тела при плоском движении. План ускорений.
10.1 Аналитический способ нахождения ускорений точек тела при плоском движении.
aMx = ẍM
aMy = ÿM
aM = 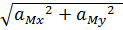 =
= 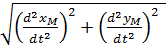
10.2 Геометрический способ нахождения ускорений точек тела при плоском движении.
a̅OA = a̅OAτ + a̅OAn
[Более подробно смотри 7 пункт в кинематике]
10.3 План ускорений
[по аналогии с планом скоростей]
11.Мгновенный центр ускорений и его свойства. Способы нахождения мгновенного центра ускорений.
11.1 Мгновенный центр ускорений и его свойства
Точка Q, ускорение которой в данный момент времени равен 0, называется мгновенным центром ускорения.
Свойства:
1: Мгновенный центр ускорения находится на отрезке, составляющим с ускорением a̅0 угол α = arctg ε/ω2, который откладывается от ускорения полюса в сторону, соответствующую направлению углового ускорения ε, на расстоянии от полюса, равном:
OQ = aO/ 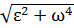
2: Если принять мгновенный центр ускорений за полюс, то ускорение любой точки будет характеризоваться только ускорением вращательном движении относительно этого полюса
3: Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгновенного центра ускорений, а векторы ускорений составляют с отрезками, соединяющими эти точки с мгновенным центром ускорений, один и тот же угол α = arctg β/ω2 [м.б. тут опечатка и угол α = arctg ε/ω2]
11.2 Способы нахождения мгновенного центра ускорений.
1. Если ускорение точки в данный момент времени равно 0, то это и есть мгновенный центр ускорения.
2. Если известны модуль и направление ускорения какой либо точки А, а так же угловая скорость ω и угловое ускорение ε, то возможны несколько случаем:
2.1 Неравномерное вращение: ω ≠ 0 и ε ≠ 0. В этом случае мгновенный центр скоростей лежит на отрезке составляющем с ускорением aA угол равный arctg ε/ω2. И лежит на расстоянии равном AQ = aA/ 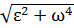
2.2 Равномерное вращение : ω ≠ 0 и ε = 0. В таком случае ускорения всех точек направлены в мгновенный центр ускорений, который находится на расстоянии от них равном AQ = 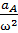
2.3 Момент, когда угловая скорость становится равной 0: ω = 0 и ε ≠ 0
Ускорения всех точек направленны перпендикулярно отрезкам соединяющим эти точки с мгновенным центром.
Расстояние до центра определяется по формуле AQ = 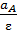
2.4 Момент, когда угловая скорость и угловое ускорение становится равными нулю при непоступательном движении: ω = 0 и ε = 0. В таком случае ускорения всех точек геометрически равны между собой и равны ускорению полюса. Мгновенный центр лежит в бесконечности.
3. Если известны модули и направление ускорений двух точек плоской фигуры.
Пусть известны ускорения точек А и B, то по теореме об ускорениях плоской фигуры, мы получим a̅B=a̅A+a̅AB. Построим в точек B параллелограмм так, чтобы aB – диагональ, aA – сторона, тогда aAB – сторона. aAB составляет с aB угол α. Отложим данный угол от aA и на пересечении двух прямых получим точку М – мгновенный центр ускорений.
| А |
| B |
| aB |
| aA |
| aAB |
| α |
| α |
| M |
| aA |
Частные случай: Если aA и aB – параллельны. То положение мгновенного центра ускорений определяется по его свойствам:
1) Модули ускорений точек пропорциональны длинам отрезков, соединяющих их с центром.
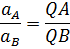
2) Ускорения точек составляют с отрезками, соединяющих их с центром, один и тот же угол.
12.Сферическое движение твёрдого тела. Углы Эйлера. Уравнения сферического движения тела.
12.1 Сферическое движение твёрдого тела
Сферическое движение твёрдого тела – движение тела, одна из точек которого во все время движения остается неподвижной.
12.2 Углы Эйлера.
Пусть дано какое-либо тело. Введем две системы координат: неподвижную Oxyz и подвижную Ouas:
| x |
| y |
| z |
| O |
| s |
| u |
| a |
| θ |
| ψ |
| φ |
| L |
Обозначим линию пересечения плоскостей Oua и Oxy примой OL
Тогда получим углы: θ = ے(z;s); ψ = ے(x;OL); φ = ے(OL;u)
Углы θ, ψ, φ – эйлеровы углы
θ – угол нутации
ψ – угол прецессии
φ – угол собственного вращения
12.3 Уравнения сферического движения тела.
При движении твердого тела, одна из точек которого остается неподвижной, углы θ, ψ, φ непрерывно изменяются во времени, являются функциями времени t:
θ = f1(t)
ψ = f2(t)
φ = f3(t)
13.Теорема Эйлера о перемещении твёрдого тела с закреплённой точкой. Мгновенная ось вращения. Угловая скорость тела.
13.1 Теорема Эйлера о перемещении твёрдого тела с закреплённой точкой
Твердое тело, имеющее одну неподвижную точку, можно переместить из одного положения в любое другое поворотом вокруг некоторой оси, проходящей через неподвижную точку
Эту ось называют осью конечного поворота твердого тела
13.2 Мгновенная ось вращения
Мгновенная ось представляет собой геометрическое место точек тела, скорость которых в данный момент равны нулю.
13.3 Угловая скорость тела.
В случае сферического движения вектор угловой скорости тела в данный момент откладывается от неподвижной точки O по мгновенной оси в такую сторону, чтобы, смотря навстречу этому вектору, видеть вращение тела происходящим против движения часовой стрелки. [ 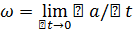 ]
]
14.Распределение скоростей точек тела при сферическом движении.
Дата: 2019-07-25, просмотров: 301.