Этот алгоритм обсчитан на компьютерах в кандидатской диссертации.
Этот алгоритм требует дополнения матрицы краевых условий U до квадратной невырожденной:
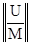
Начальные значения Y  (0), Y
(0), Y 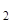 (0), Y
(0), Y 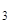 (0), Y
(0), Y 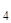 (0), Y*(0) находятся из решения следующих систем линейных алгебраических уравнений:
(0), Y*(0) находятся из решения следующих систем линейных алгебраических уравнений:
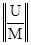 ∙ Y*(0) =
∙ Y*(0) = 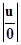 ,
,
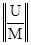 ∙ Y
∙ Y 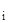 (0) =
(0) = 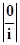 , где i =
, где i = 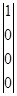 ,
, 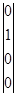 ,
, 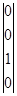 ,
, 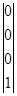 ,
,
где 0 – вектор из нулей размерности 4х1.
Замена метода численного интегрирования Рунге-Кутта в методе прогонки С.К.Годунова
Эта замена формул Рунге-Кутта на формулу теории матриц обсчитана на компьютерах в кандидатской диссертации.
В методе С.К.Годунова как показано выше решение ищется в виде:
Y(x) = Y 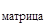 (x) ∙ c + Y*(x).
(x) ∙ c + Y*(x).
На каждом конкретном участке метода прогонки С.К.Годунова между точками ортогонализации можно вместо метода Рунге-Кутта пользоваться теорией матриц и выполнять расчет через матрицу Коши:
Y 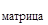 (x
(x 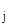 ) = K(x
) = K(x 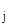 - x
- x 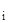 ) ∙Y
) ∙Y 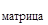 (x
(x 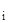 ).
).
Так выполнять вычисления быстрее, особенно для дифференциальных уравнений с постоянными коэффициентами.
И аналогично через теорию матриц можно вычислять и вектор Y*(x) частного решения неоднородной системы дифференциальных уравнений. Или для этого вектора отдельно можно использовать метод Рунге-Кутта, то есть можно комбинировать теорию матриц и метод Рунге-Кутта.
Метод половины констант
Этот метод пока не обсчитан на компьютерах.
Выше было показано, что решение системы линейных обыкновенных дифференциальных уравнений можно искать в виде только с половиной возможных векторов и констант. Была приведена формула для начала вычислений:
Y(0) = М 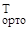 ∙с +
∙с + 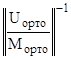 ∙
∙ 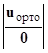 .
.
Из теории матриц известно, что если матрица ортонормирована, то её обратная матрица есть её транспонированная матрица. Тогда последняя формула приобретает вид:
Y(0) = М 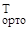 ∙с + U
∙с + U 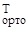 ∙u
∙u 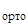
или
Y(0) = U 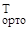 ∙u
∙u 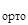 + М
+ М 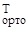 ∙с
∙с
или
Y(0) = 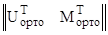 ∙
∙ 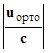 ,
,
Таким образом записана в матричном виде формула для начала счета с левого края, когда на левом крае удовлетворены краевые условия.
Далее запишем V∙Y(1) = v и Y(1) = K(1←0) ∙Y(0) + Y*(1←0) совместно:
V∙ [ K(1←0) ∙Y(0) + Y*(1←0) ] = v
V∙ K(1←0) ∙Y(0) = v - V∙Y*(1←0)
и подставим в эту формулу выражение для Y(0):
V∙ K(1←0) ∙ 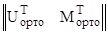 ∙
∙ 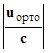 = v - V∙Y*(1←0).
= v - V∙Y*(1←0).
V∙ K(1←0) ∙ 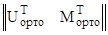 ∙
∙ 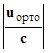 = p.
= p.
Таким образом мы получили выражение вида:
D ∙ 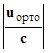 = p,
= p,
где матрица D имеет размерность 4х8 и может быть естественно представлена в виде двух квадратных блоков размерности 4х4:
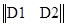 ∙
∙ 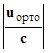 = p.
= p.
Тогда можем записать:
D1∙ u 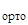 + D2 ∙ c = p.
+ D2 ∙ c = p.
Отсюда получаем, что:
c = D2 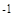 ∙ ( p - D1∙ u
∙ ( p - D1∙ u  )
)
Таким образом, искомые константы найдены.
Далее показано как применять этот метод для решения «жестких» краевых задач.
Запишем
V∙ K(1←0) ∙ 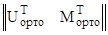 ∙
∙ 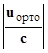 = p.
= p.
совместно с K(1←0) = K(1←x2) ∙ K(x2←x1) ∙ K(x1←0) и получим:
V∙ K(1←x2) ∙ K(x2←x1) ∙ K(x1←0) ∙ 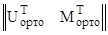 ∙
∙ 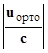 = p.
= p.
Эту систему линейных алгебраических уравнений можно представить в виде:
[ V∙ K(1←x2) ] ∙ { K(x2←x1) ∙ K(x1←0) ∙ 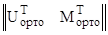 ∙
∙ 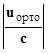 } = p.
} = p.
[ матрица ] ∙ { вектор } = вектор
Эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки [матрицы] ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:
[ V∙ K(1←x2) ] 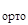 {K(x2←x1) ∙ K(x1←0) ∙
{K(x2←x1) ∙ K(x1←0) ∙ 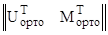
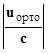 } =p
} =p 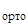 .
.
И так далее.
В итоге поочередного вычленений матриц слева из вектора и ортонормирования получим систему:
D 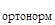 ∙
∙ 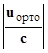 = p
= p 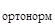 ,
,
Отсюда получаем, что:
c = D2 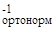 ∙ (p
∙ (p 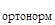 - D1
- D1 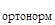 ∙ u
∙ u 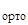 )
)
Таким образом, искомые константы найдены.
Дата: 2019-07-25, просмотров: 308.