Введение
На примере системы дифференциальных уравнений цилиндрической оболочки ракеты – системы обыкновенных дифференциальных уравнений 8-го порядка (после разделения частных производных).
Система линейных обыкновенных дифференциальных уравнений имеет вид:
Y 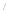 (x) = A(x) ∙ Y(x) + F(x),
(x) = A(x) ∙ Y(x) + F(x),
где Y(x) – искомая вектор-функция задачи размерности 8х1, Y 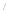 (x) – производная искомой вектор-функции размерности 8х1, A(x) – квадратная матрица коэффициентов дифференциального уравнения размерности 8х8, F(x) – вектор-функция внешнего воздействия на систему размерности 8х1.
(x) – производная искомой вектор-функции размерности 8х1, A(x) – квадратная матрица коэффициентов дифференциального уравнения размерности 8х8, F(x) – вектор-функция внешнего воздействия на систему размерности 8х1.
Здесь и далее вектора обозначаем жирным шрифтом вместо черточек над буквами
Краевые условия имеют вид:
U∙Y(0) = u,
V∙Y(1) = v,
где
Y(0) – значение искомой вектор-функции на левом крае х=0 размерности 8х1, U – прямоугольная горизонтальная матрица коэффициентов краевых условий левого края размерности 4х8, u – вектор внешних воздействий на левый край размерности 4х1,
Y(1) – значение искомой вектор-функции на правом крае х=1 размерности 8х1, V – прямоугольная горизонтальная матрица коэффициентов краевых условий правого края размерности 4х8, v – вектор внешних воздействий на правый край размерности 4х1.
В случае, когда система дифференциальных уравнений имеет матрицу с постоянными коэффициентами A=const, решение задачи Коши имеет вид [Гантмахер]:
Y(x) = e 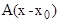 ∙ Y(x
∙ Y(x  ) + e
) + e 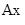 ∙
∙ 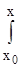 e
e 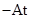 ∙ F(t) dt,
∙ F(t) dt,
где
e 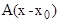 = E + A(x-x
= E + A(x-x  ) + A
) + A 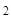 (x-x
(x-x  )
) 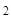 /2! + A
/2! + A 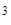 (x-x
(x-x  )
) 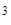 /3! + …,
/3! + …,
где E это единичная матрица.
Матричная экспонента ещё может называться матрицей Коши или матрициантом и может обозначаться в виде:
K(x←x  ) = K(x - x
) = K(x - x  ) = e
) = e 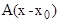 .
.
Тогда решение задачи Коши может быть записано в виде:
Y(x) = K(x←x  ) ∙ Y(x
) ∙ Y(x  ) + Y*(x←x
) + Y*(x←x  ) ,
) ,
где Y*(x←x  ) = e
) = e 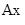 ∙
∙ 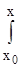 e
e 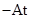 ∙ F(t) dt это вектор частного решения неоднородной системы дифференциальных уравнений.
∙ F(t) dt это вектор частного решения неоднородной системы дифференциальных уравнений.
Случай переменных коэффициентов
Этот вариант рассмотрения переменных коэффициентов проверялся в кандидатской диссертации.
Из теории матриц [Гантмахер] известно свойство перемножаемости матричных экспонент (матриц Коши):
e 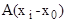 = e
= e 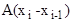 ∙ e
∙ e 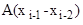 ∙ … ∙ e
∙ … ∙ e 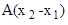 ∙ e
∙ e 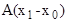 ,
,
K(x 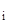 ←x
←x  ) = K(x
) = K(x 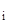 ←x
←x 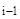 ) ∙ K(x
) ∙ K(x 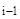 ←x
←x 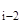 ) ∙ … ∙ K(x
) ∙ … ∙ K(x 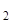 ←x
←x 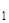 ) ∙ K(x
) ∙ K(x 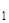 ←x
←x  ).
).
В случае, когда система дифференциальных уравнений имеет матрицу с переменными коэффициентами A=A(x), решение задачи Коши предлагается искать при помощи свойства перемножаемости матриц Коши. То есть интервал интегрирования разбивается на малые участки и на малых участках матрицы Коши приближенно вычисляются по формуле для постоянной матрицы в экспоненте. А затем матрицы Коши, вычисленные на малых участках, перемножаются:
K(x 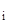 ←x
←x  ) = K(x
) = K(x 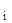 ←x
←x 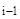 ) ∙ K(x
) ∙ K(x 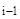 ←x
←x 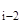 ) ∙ … ∙ K(x
) ∙ … ∙ K(x 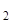 ←x
←x 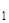 ) ∙ K(x
) ∙ K(x 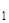 ←x
←x  ),
),
где матрицы Коши приближенно вычисляются по формуле:
K(x 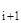 ←x
←x 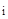 ) = e
) = e 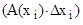 , где ∆x
, где ∆x 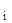 = x
= x 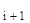 - x
- x 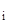 .
.
Метод половины констант
Этот метод пока не обсчитан на компьютерах.
Выше было показано, что решение системы линейных обыкновенных дифференциальных уравнений можно искать в виде только с половиной возможных векторов и констант. Была приведена формула для начала вычислений:
Y(0) = М 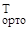 ∙с +
∙с + 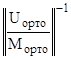 ∙
∙ 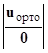 .
.
Из теории матриц известно, что если матрица ортонормирована, то её обратная матрица есть её транспонированная матрица. Тогда последняя формула приобретает вид:
Y(0) = М 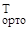 ∙с + U
∙с + U 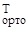 ∙u
∙u 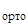
или
Y(0) = U 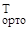 ∙u
∙u 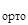 + М
+ М 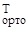 ∙с
∙с
или
Y(0) = 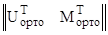 ∙
∙ 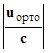 ,
,
Таким образом записана в матричном виде формула для начала счета с левого края, когда на левом крае удовлетворены краевые условия.
Далее запишем V∙Y(1) = v и Y(1) = K(1←0) ∙Y(0) + Y*(1←0) совместно:
V∙ [ K(1←0) ∙Y(0) + Y*(1←0) ] = v
V∙ K(1←0) ∙Y(0) = v - V∙Y*(1←0)
и подставим в эту формулу выражение для Y(0):
V∙ K(1←0) ∙ 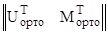 ∙
∙ 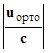 = v - V∙Y*(1←0).
= v - V∙Y*(1←0).
V∙ K(1←0) ∙ 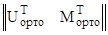 ∙
∙ 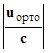 = p.
= p.
Таким образом мы получили выражение вида:
D ∙ 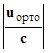 = p,
= p,
где матрица D имеет размерность 4х8 и может быть естественно представлена в виде двух квадратных блоков размерности 4х4:
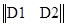 ∙
∙ 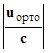 = p.
= p.
Тогда можем записать:
D1∙ u 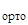 + D2 ∙ c = p.
+ D2 ∙ c = p.
Отсюда получаем, что:
c = D2 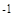 ∙ ( p - D1∙ u
∙ ( p - D1∙ u 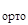 )
)
Таким образом, искомые константы найдены.
Далее показано как применять этот метод для решения «жестких» краевых задач.
Запишем
V∙ K(1←0) ∙ 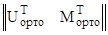 ∙
∙ 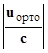 = p.
= p.
совместно с K(1←0) = K(1←x2) ∙ K(x2←x1) ∙ K(x1←0) и получим:
V∙ K(1←x2) ∙ K(x2←x1) ∙ K(x1←0) ∙ 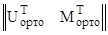 ∙
∙ 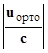 = p.
= p.
Эту систему линейных алгебраических уравнений можно представить в виде:
[ V∙ K(1←x2) ] ∙ { K(x2←x1) ∙ K(x1←0) ∙ 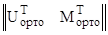 ∙
∙ 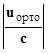 } = p.
} = p.
[ матрица ] ∙ { вектор } = вектор
Эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки [матрицы] ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:
[ V∙ K(1←x2) ] 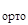 {K(x2←x1) ∙ K(x1←0) ∙
{K(x2←x1) ∙ K(x1←0) ∙ 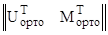
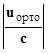 } =p
} =p 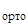 .
.
И так далее.
В итоге поочередного вычленений матриц слева из вектора и ортонормирования получим систему:
D 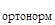 ∙
∙ 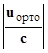 = p
= p 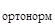 ,
,
Отсюда получаем, что:
c = D2 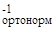 ∙ (p
∙ (p 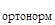 - D1
- D1 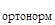 ∙ u
∙ u 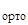 )
)
Таким образом, искомые константы найдены.
Введение
На примере системы дифференциальных уравнений цилиндрической оболочки ракеты – системы обыкновенных дифференциальных уравнений 8-го порядка (после разделения частных производных).
Система линейных обыкновенных дифференциальных уравнений имеет вид:
Y 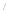 (x) = A(x) ∙ Y(x) + F(x),
(x) = A(x) ∙ Y(x) + F(x),
где Y(x) – искомая вектор-функция задачи размерности 8х1, Y 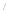 (x) – производная искомой вектор-функции размерности 8х1, A(x) – квадратная матрица коэффициентов дифференциального уравнения размерности 8х8, F(x) – вектор-функция внешнего воздействия на систему размерности 8х1.
(x) – производная искомой вектор-функции размерности 8х1, A(x) – квадратная матрица коэффициентов дифференциального уравнения размерности 8х8, F(x) – вектор-функция внешнего воздействия на систему размерности 8х1.
Здесь и далее вектора обозначаем жирным шрифтом вместо черточек над буквами
Краевые условия имеют вид:
U∙Y(0) = u,
V∙Y(1) = v,
где
Y(0) – значение искомой вектор-функции на левом крае х=0 размерности 8х1, U – прямоугольная горизонтальная матрица коэффициентов краевых условий левого края размерности 4х8, u – вектор внешних воздействий на левый край размерности 4х1,
Y(1) – значение искомой вектор-функции на правом крае х=1 размерности 8х1, V – прямоугольная горизонтальная матрица коэффициентов краевых условий правого края размерности 4х8, v – вектор внешних воздействий на правый край размерности 4х1.
В случае, когда система дифференциальных уравнений имеет матрицу с постоянными коэффициентами A=const, решение задачи Коши имеет вид [Гантмахер]:
Y(x) = e 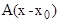 ∙ Y(x
∙ Y(x  ) + e
) + e 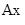 ∙
∙ 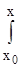 e
e 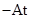 ∙ F(t) dt,
∙ F(t) dt,
где
e 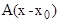 = E + A(x-x
= E + A(x-x  ) + A
) + A 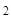 (x-x
(x-x  )
) 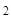 /2! + A
/2! + A 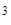 (x-x
(x-x  )
) 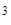 /3! + …,
/3! + …,
где E это единичная матрица.
Матричная экспонента ещё может называться матрицей Коши или матрициантом и может обозначаться в виде:
K(x←x  ) = K(x - x
) = K(x - x  ) = e
) = e 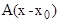 .
.
Тогда решение задачи Коши может быть записано в виде:
Y(x) = K(x←x  ) ∙ Y(x
) ∙ Y(x  ) + Y*(x←x
) + Y*(x←x  ) ,
) ,
где Y*(x←x  ) = e
) = e 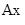 ∙
∙ 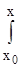 e
e 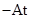 ∙ F(t) dt это вектор частного решения неоднородной системы дифференциальных уравнений.
∙ F(t) dt это вектор частного решения неоднородной системы дифференциальных уравнений.
Случай переменных коэффициентов
Этот вариант рассмотрения переменных коэффициентов проверялся в кандидатской диссертации.
Из теории матриц [Гантмахер] известно свойство перемножаемости матричных экспонент (матриц Коши):
e 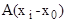 = e
= e 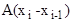 ∙ e
∙ e 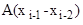 ∙ … ∙ e
∙ … ∙ e 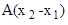 ∙ e
∙ e 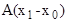 ,
,
K(x 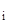 ←x
←x  ) = K(x
) = K(x 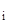 ←x
←x 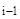 ) ∙ K(x
) ∙ K(x 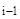 ←x
←x 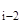 ) ∙ … ∙ K(x
) ∙ … ∙ K(x 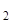 ←x
←x 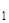 ) ∙ K(x
) ∙ K(x 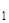 ←x
←x  ).
).
В случае, когда система дифференциальных уравнений имеет матрицу с переменными коэффициентами A=A(x), решение задачи Коши предлагается искать при помощи свойства перемножаемости матриц Коши. То есть интервал интегрирования разбивается на малые участки и на малых участках матрицы Коши приближенно вычисляются по формуле для постоянной матрицы в экспоненте. А затем матрицы Коши, вычисленные на малых участках, перемножаются:
K(x 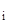 ←x
←x  ) = K(x
) = K(x 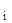 ←x
←x 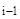 ) ∙ K(x
) ∙ K(x 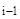 ←x
←x 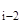 ) ∙ … ∙ K(x
) ∙ … ∙ K(x 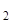 ←x
←x 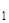 ) ∙ K(x
) ∙ K(x 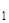 ←x
←x  ),
),
где матрицы Коши приближенно вычисляются по формуле:
K(x 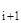 ←x
←x 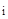 ) = e
) = e 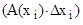 , где ∆x
, где ∆x 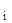 = x
= x 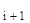 - x
- x 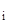 .
.
Дата: 2019-07-25, просмотров: 284.