Зубчатые колеса изготавливаются двумя методами: 1) метод копирования. Состоит в том, что по чертежам тщательно изготавливается дисковая фреза. Режущая кромка фрезы имеет очертание впадины между зубьями. Вращаясь, фреза перемещается в направлении боковой образующей зуба. За каждый ход фрезы вдоль оси колеса получается нарезанной одна впадина. По прохождении всей впадины фреза возвращается в исходное положение. После этого нарезаемое колесо поворачивается на величину угла t=2p/z, где z–число зубьев нарезаемого колеса и процесс повторяется. 2) метод огибания и метод обкатки. Этот метод заключается в том, режущему инструменту и заготовке сообщают то относительное движение, которое имели бы 2 зубчатых колеса, находящихся в правильном зацеплении. В таком случае режущий инструмент должен представлять собой также зубчатое колесо. Такое колесо инструмент носит название долбяк, который совершает поступательное движение параллельно оси х-х нарезаемого колеса. Одновременно долбяку и колесу сообщается вращательное движение с соотношением угловых скоростей, как если бы долбяк и колесо находятся в зацеплении. Практически долбление происходит последовательно этап за этапом, а не непрерывно: долбяк движется вверх и вниз, поворачивается нарезаемое колесо и т.д. Тогда профиль нарезаемого колеса получается как огибающая всех положений режущей кромки долбяка, т.е. инструмент как бы обкатывает нарезаемое колесо (позволяет вырезать колеса с внутренним зацеплением). Первый метод более простой, второй требует специального дорогостоящего оборудования и является более точным.

Нарезание производящей рейкой без смещения. Геометрический расчет таких колес

Так как для любого колеса может быть спроектирована сопряженная с колесом рейка, то вместо колеса-инструмента в качестве использована рейка. Рейка совершает в вертикальном направлении возвратно-поступательное движение, параллельное оси нарезаемого колеса. Заготовка имеет двойное движение в горизонтальной плоскости. Вращаясь вокруг оси, она одновременно перемещается вдоль рейки. Таким образом, заготовка осуществляет движение колеса относительно рейки, и профили зубьев нарезаемого колеса получаются процессом обкатывания. Геометрический расчет зубчатых колес без смещения:

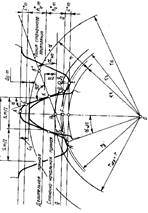
Делительная прямая делит шаг рейки пополам. Шаг рейки равен p=pm, h_a^*–коэффициент высоты зуба, c* – коэффициент радиального зазора. h_a = h_a^*m, c = c^*m, m –стандартный модуль. h_a – высота головки зуба,

h_a=(h_a^*+X–Dy)m – для случая со смещением, X – коэффициент смещения, Dy– коэффициент уравнительного смещения, h_f – высота ножки зуба. h_f = (h_a^*–X+C^*)m – для случая со смещением, d_a – окружности вершин зубьев, d_a =d+2h_a=mz+2(h_a^*+X–Dy)m, d_f–диаметр окружности впадин зубьев, d_f = d–2h_f= mz-2(h_a^*–X + C^*)m, d– диаметр делительной окружности.

Минимальное число зубьев шестерни без подрезания. Основные причины введения смещения при нарезании зубчатых колес

PB£PN, PB×sina=h_a^*m, PB=h_a^*m/sina, PN = mz/2×sina, h_a^*m/sina£mz/2sina, Z_min =2h_a^*/sin²a=2×1/sin²20°= 17,097»17

Причины введения смещения инструментальной рейки при нарезании зубчатых колес следующие: 1) устранение подрезания (подрезание уменьшает эвольвентную часть профиля зуба и ослабляет его опасное сечение; 2) увеличение прочности зуба; 3) вписывание в заданные межосевые расстояния.

Определение минимального коэф-та смещения. Два вида геометрического расчета зубчатых колес при смещении (дано: 1) z ₁ , z ₂ , m , α , x ₁ , x ₂ ; 2) z ₁ , z ₂ , m , α , α_W )

PB£PN, PB×sina=(h_a^*–X)m, PB=mz/2 ×sina, (h_a^*–X)m/sina£mz/2 × sina,

h_a*–z/2 ×sin²a £ X, X_min=h_a^*[1–z/ (2h_a^*/

/sin²a)]. Минимальное число зубьев , своб. от подрезания равно 17, Þ, X_min = h_a^*(z_min–z)/z_min, т.к. h_a^*=1, то X_min=(z_min-z)/z_min = (17-z)/17.

Расчет зубчатых колес

1) α_W – угол зацепления, α – угол рейки. inv α_W = inv α + 2x_Σtgα/(z₁+z₂), inv α_W = tg α_W – α_W (инвалюта). a_W – межосевое расстояние при смещении, a – межосевое расстояние без смещения. a_W=a×cosα/cosα_W, a=r₁+ r₂, r₁ – радиус делительной окружности шестерни, r₂ – радиус делительной окружности зубчатого колеса. a=r₁+r₂=(m/2)(z₁+z₂). y – коэф-т воспринимаемого смещения. ym=α_W-a, y=(α_W-a)/m. Δy – коэф-т уравнительного смещения.

½mz₁+½mz₂+ym=½mz₁+(h_a^*+x₁+Dy)m+ ½mz₂–(h_a^*–x₂+c^*)m+c^*m

a_W=r₁+r₂+ym, a_W=r_1a+r_f2+c^*m,

сократив одинаковые выражения в левой и правой частях уравнения и разделив все на m, получим: y=x₁+x₂-Δy x₁+x₂=x_Σ – суммарный коэф-т смещения,

Δy= x_Σ–y

2) a_W = a∙cosα/cosα_W,

α_W = arccos(a∙cosα/a_W),

inv α_W = inv α + 2x_Σtgα/(z₁+z₂)

x_Σ=(invα_W – invα)(z₁+z₂)/2tgα

y=(α_W-a)/m. Δy= x_Σ–y