Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

План ускорений

 

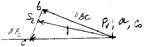
План скоростей

 

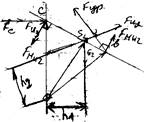
Рычаг Жуковского

 

M_И2 = F_МИ2 ×ℓ_BC, F_MИ2 = M_И2/ℓ_BC,

 

Момент на рычаге Жуковского:

 

m_V(F_ур(ab) +F_MИ2(bc)–G₂h₁–F_И2h₂–(F_C+F_И3)p_Vc)=0,

F_ур= (–F_МИ2×bc+G₂h₁+F_И2h₂ +(F_C+F_И3)p_Vc)/ab

 

Уравновешивание рычажных механизмов

 

Метод замещающих масс:

 

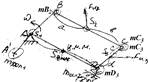
Сместим центр масс звена АВ в точку А путем некоторого противовеса у точки А. Тоже самое проделываем для звена CD.

 

1)m₁ + m₂+ m₃ + m₄ = M

2) Sm_ix_i = 0

3) Sm_iy_i = 0

 

Выше написанное является условием смещения центра масс.

 

4) Sm_i(x_i²+y_i²)=J_s

 

Для второго звена: m_B2×a = m_C2×b –статические моменты,

 

m_B2(a+b) = m_C2b, m_C2 = m×b/(a+b), m_C2=m₂×a/(a+b).

 

Для третьего звена:

 

m_C3 = m₃×d/(c+d), m_D3 = m₃×c/(c+d)

 

Рассмотрим равновесие первого звена:

 

m_B2×AB = m_доп1×AA¢, m_доп1=m_B2AB/AA¢, (m_C2+m_C3)×CD = m_доп2×DD¢, m_доп2 = (m_С2+m_С3)×CD/DD¢, (m_B2+m_доп1)AS_цмм = (m_C2+m_C3+m_D+m_доп2)DS_цмм, m_SAAD = (m_SA+m_SD)SD, SD = AD×M_SA/(m_SA+m_SD)

 

Уравнение удовлетворяет трем условиям: сумма по оси x и y = 0, сумма всех масс = общей массе.

Расчет зубчатых колес

1) α_W – угол зацепления, α – угол рейки. inv α_W = inv α + 2x_Σtgα/(z₁+z₂), inv α_W = tg α_W – α_W (инвалюта). a_W – межосевое расстояние при смещении, a – межосевое расстояние без смещения. a_W=a×cosα/cosα_W, a=r₁+ r₂, r₁ – радиус делительной окружности шестерни, r₂ – радиус делительной окружности зубчатого колеса. a=r₁+r₂=(m/2)(z₁+z₂). y – коэф-т воспринимаемого смещения. ym=α_W-a, y=(α_W-a)/m. Δy – коэф-т уравнительного смещения.

 

½mz₁+½mz₂+ym=½mz₁+(h_a^*+x₁+Dy)m+ ½mz₂–(h_a^*–x₂+c^*)m+c^*m

a_W=r₁+r₂+ym, a_W=r_1a+r_f2+c^*m,

 

сократив одинаковые выражения в левой и правой частях уравнения и разделив все на m, получим: y=x₁+x₂-Δy x₁+x₂=x_Σ – суммарный коэф-т смещения,

 

Δy= x_Σ–y

2) a_W = a∙cosα/cosα_W,

α_W = arccos(a∙cosα/a_W),

inv α_W = inv α + 2x_Σtgα/(z₁+z₂)

x_Σ=(invα_W – invα)(z₁+z₂)/2tgα

y=(α_W-a)/m. Δy= x_Σ–y

Коэф-т перекрытия. Определение его графическим и аналитическим методами

Коэф-т перекрытия определяет плавность работы зубчатой передачи и показывает среднее значение числа пар сопряжения зубьев, находящихся в сопряжении. Такие качества передачи обеспечиваются перекрытием работы одной пары зубьев работой другой пары. Для этого каждая последующая пара зубьев должна войти в зацепления еще до того, как предшествующая пара выйдет из зацепления. E=B₁B₂/πmcosα, πm – шаг по делительной окружности, πmcosα – шаг по основной окружности, B₁B₂ – часть линии зацепления ограничительной окружности вершин зубьев шестерни зубчатого колеса, которая называется активной частью линии зацепления.

 

Аналитический метод. B₁B₂=B₁P+PB₂=B₁N₁–PN₁+BN₂–PN₂=√(r²_a1–r²_b1)+√(r²_a2–r²_b2)–N₁N₂,

N₁N₂= r_W1sinα_W+r_W2sinα_W=a_Wsinα_W

 

r_W1, r_W2 – радиусы начальных окруж.

 

 

E > 0 должно быть всегда. Для обычных передач Е ≈ 1,3. Чем больше число зубьев, тем больше Е.

Графический метод

О величине перекрытия судят по коэффициенту перекрытия, который выражают отношением угла торцового перекрытия к угловому шагу. Угол торцового зацепления a – это угол поворота колеса от положения зубьев при входе в зацепление. Следовательно,

 

Е = j_а1/t₁,

 

где t₁=2p/z₁– угловой шаг.

 

 

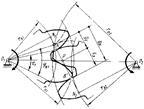
Если Е<1, то непрерывности зацепления зубьев не будет.

 

Условие статической определимости системы

 

3n=2p₁+p₂ – усилие статической определимости, число усилий = число неизвестных. Чаще 3n = 2p₁, т.к. p₂ = 0, условие существований групп Ассура (DW=3n–2p₁ = 0).

 

Определение сил инерции и моментов от сил инерции

 

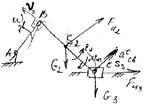
S₂ – центр масс 2-го звена

 

 

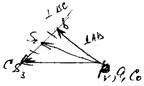
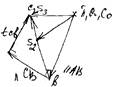
F_И2= –m₂×a_S2 = – m₂(nS₂)m_a , M_И2

(момент от силы инерции)= –J_S2×E₂ = –J_S2×(t_cb)m_a/

/ℓ_CB, F_И3 = –m₃a_S3 = –m₃(pS₃)m_a = 0.

 

Силовой расчет первой группы Ассура

 

 

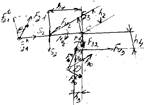
F₃₀ – сила в точке D со стороны отброшенной опоры 0; F₂₁ – сила, действующая со стороны первого (отброшенного) звена на второе. Разложим силы F₂₁ и F₃₀ – на второе путем проецирования их на соответствующие звенья 2 и 3. 1)F₂₁^t, SM_C =0 (равновесие 2-го звена):

 

F₂₁^t (BC)×m_ℓ–G₂h₁×m_ℓ+F_И2h₂×m_ℓ + M_И2=0,

F₂₁^t=(G₂h₁m_ℓ–F_И2h₂m_ℓ–M_И2)/[(BC)×m_ℓ].

2)F₃₀^t, SM_C=0 (равновесие 3-го звена):

F₃₀^t(CD)m_ℓ + G₂h₃m_ℓ + F_И3h₄m_ℓ – M_И3=0,

F₃₀^t=[–G₂h₃m_ℓ – F₄h₄m_ℓ + M_И3] / [(CD)m_ℓ].

3)F₂₁ⁿ, F₃₀ⁿ, SF=0 (равновесие звена 2 и 3):

F₂₁ⁿ+F₂₁^t+G₂+F_И2+G₃+F_И3+F₃₀^t+F₃₀ⁿ = 0.

 

Величины искомых сил известны, но не известны их направления.

4)F₂₃, SF=0 (равновесие звена 2 и 3):

 

F₂₁ⁿ + F₂₁^t + G₂ + F₂₃=0.

 

Далее определяем значение уравновешивающей силы на начальном звене:

 

 

F₁₀ – сила со стороны отброшенной опоры 0 на звено 1.

5) F_ур, SM_A = 0: F_ур(АВ)m_ℓ–F₁₂h₁m_ℓ = 0, т.к. на звене формально нет момента, то m_ℓ можно не писать, т.е получим F_ур(АВ) – F₁₂h₁=0

6) F₁₀, SF = 0: F_ур+F₁₂+F₁₀ = 0

 

 

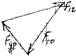
Рисуем все известные силы последовательно, учитывая величины и направления. Т.к. SF=0, то соединив конец вектора силы F₁₂ и начало F_ур получим искомую силу F₁₀.

 

Силовой расчет группы Ассура 2-го вида

 

 

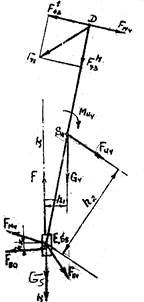
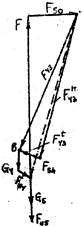
F₄₃ – сила, действующая со стороны третьего (отброшенного) звена на четвертое.

1) F₄₃^t, SM_E = 0 (равновесие звена 4): F₄₃^t(DE)m_ℓ–G₄h₁m_ℓ–F_И4h₂m_ℓ–M_И4=0

 

F₄₃^t=(G₄h₁m_ℓ+F_И4h₂m_ℓ+М_И4)/(DE)m_ℓ

 

2) F₅₀,F₄₃ⁿ, SF = 0 (равновесие звена 4):

 

F₄₃ⁿ + F₄₃^t + G₄ + F_И4 + G₅ + F_И5 + F + F₅₀=0

 

3) F₅₄, SF = 0 (равновесие звена 5):

 

G₅ + F_И5 + F + F₅₀ + F₅₄=0.

 

4) h_x, SM_E=0 (равновесие звена5): F₅₀×h_xm_ℓ=0, h_x=0.

 

Силовой расчет группы Ассура 3-го вида

 

 

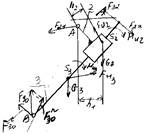
1)F₃₀^t, SM_A=0 (равновесие звена 2 и 3)

2)F₃₀ⁿ, F³², SF=0 (равновесие звена 3):

 

F₃₀ⁿ + F₂₀ⁿ +G₃ +F_И3 + F₃₂= 0

 

 

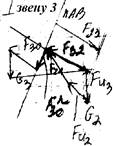
3) F₂₁, SF=0 (равновесие звена 3):

 

F₂₃ + G₂ + F_И2 + F₂₁=0

 

4)h_X, SM_A=0 (равновесие звена 2):

 

F₂₃×h_xm_ℓ + M_И2 + G₂h₁m_ℓ – F_И2h₂m_ℓ =0,

h_x = [–М_И2 – G₂h₁m_ℓ + F_И2h₂m_ℓ] / (F₂₃m_ℓ)

 

Силовой расчет группы Ассура 4-го вида

 

 

1)F₂₁ и F₃₄, SF=0 (равновесие звеньев 2 и 3):

 

F₂₁ + G₂ + F_И2 + G₃ + F_И3 + F₃₄=0

 

 

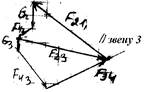
2)F₂₃, SF=0 (равновесие звеньев 2 (3)):

F₂₁+G₂+F_И2+F₂₃=0

3)h_x1, SM_B=0 (равновесие звена 2):

F₂₁h_x1–G₂h₁+F_И2×h₂=0, h_x1=(G₂h₁–F_И2h₂)/F₂₁

4)h_x2, SM_B=0 (равновесие звена 3):

F₃₄×h_x2–G₃h₃+F_И3×h₄=0

 

Силовой расчет группы Ассура 5-го вида

 

 

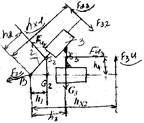
1)F₃₂ и F₃₄, SF=0 (равновесие звена 3):

F₃₄ + G₃ + F_И3 + F₃₄ = 0

 

 

2)F₂₁, SF=0 (равновесие звена 2):

F₂₃ + G₂ + F_И2 + F₂₁ = 0

 

 

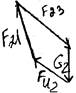
3)h_x1, SM_B=0 (равновесие звена 2):

F₂₃h_x1–G₂h₁+F_И2h₂=0, h_x1=G₂h₁+F_И2h₂=0

4)h_X2, SM_B=0 (равновесие 2 и 3):

F₃₄h_X2–G₃h₃–F_И3h₄–G₂h₁+F_И2h₂=0

h_X2=(G₃h₃+F_И3h₄+G₂h₁–F_И2h₂)/F₃₄.

 

Силовой расчет с учетом сил трения

 

Если учитывают силы трения, то сначала расчет производится без учета трения, а во втором расчете рассчитывают эти силы трения.

 

F_тр=F₃₄×f,

 

где f – коэффициент трения

 

Определение уравновешивающей силы

 

Уравновешивающая сила определяется по рычагу Жуковского. Рычагом Жуковского называется повернутый на 90° план скоростей (желательно против направления вращения начального звена), к которому прикладывают все силы, действующие на механизм без изменения их направления и ищется равновесие этого рычага по принципу Лагранжа (для равновесия твердого тела необходимо, чтобы сумма работ равнялась нулю), т.е.

SF_i×dS_Dicos(F_i, dS_Di) = 0, SF_idS_Dicos(F_i,dS_Di)=0, точка D – точка, лежащая на звене к которой приложена сила F. Разделим все на dt:

 

SF_i×V_Dicos(F_i, V_Di) = 0

 

Для равновесия твердых тел необходимо и достаточно, чтобы мощность всех действующих на систему сил равнялась нулю. P = F₂V_S2cos a= F₂(P_VS₂)m_Vcos a.

 

 

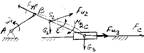
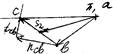
План ускорений

 

План скоростей

 

Рычаг Жуковского

 

M_И2 = F_МИ2 ×ℓ_BC, F_MИ2 = M_И2/ℓ_BC,

 

Момент на рычаге Жуковского:

 

m_V(F_ур(ab) +F_MИ2(bc)–G₂h₁–F_И2h₂–(F_C+F_И3)p_Vc)=0,

F_ур= (–F_МИ2×bc+G₂h₁+F_И2h₂ +(F_C+F_И3)p_Vc)/ab

 

Уравновешивание рычажных механизмов

 

Метод замещающих масс:

 

Сместим центр масс звена АВ в точку А путем некоторого противовеса у точки А. Тоже самое проделываем для звена CD.

 

1)m₁ + m₂+ m₃ + m₄ = M

2) Sm_ix_i = 0

3) Sm_iy_i = 0

 

Выше написанное является условием смещения центра масс.

 

4) Sm_i(x_i²+y_i²)=J_s

 

Для второго звена: m_B2×a = m_C2×b –статические моменты,

 

m_B2(a+b) = m_C2b, m_C2 = m×b/(a+b), m_C2=m₂×a/(a+b).

 

Для третьего звена:

 

m_C3 = m₃×d/(c+d), m_D3 = m₃×c/(c+d)

 

Рассмотрим равновесие первого звена:

 

m_B2×AB = m_доп1×AA¢, m_доп1=m_B2AB/AA¢, (m_C2+m_C3)×CD = m_доп2×DD¢, m_доп2 = (m_С2+m_С3)×CD/DD¢, (m_B2+m_доп1)AS_цмм = (m_C2+m_C3+m_D+m_доп2)DS_цмм, m_SAAD = (m_SA+m_SD)SD, SD = AD×M_SA/(m_SA+m_SD)

 

Уравнение удовлетворяет трем условиям: сумма по оси x и y = 0, сумма всех масс = общей массе.