2.1.Классическое описание условий магнитного резонанса.

Вращающийся заряд q можно рассматривать как кольцевой ток, поэтому он ведет себя как магнитный диполь, величина момента равна:

m=iS,                                                                                                                (2.1)

где i-сила эквивалентного тока;

S - площадь, охватываемая кольцевым током.

В соответствии с понятием силы тока имеем:

i=qn,

где n=v/2pr-число оборотов заряда q в секунду;

v-линейная скорость;

r-радиус окружности, по которой движется заряд.

Если перейти к электромагнитным единицам (т.е. разделить заряд на с) и учесть, что S=pr², то выражение (2.1) можно переписать в следующем виде:

m=qvr/2c.                                                                                                         (2.2)

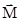Вращающаяся частица с массой М обладает угловым моментом (или моментом импульса) L, представляющим собой вектор, направленный вдоль оси вращения и имеющий величину Mvr. Здесь L=[rp]= [rv], в данном случае r^v. И заряд, и масса участвуют в одном и том же вращении (вращательном движении), поэтому вектор магнитного момента коллинеарен вектору углового момента, с которым он связан соотношением

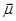=(q/2Mc)L=gL,                                                                                            (2.3)

где g=q/2Mc-гиромагнитное отношение, являющееся индивидуальной характеристикой частицы (ядра).

Рассматриваемая здесь модель, естественно, не может объяснить ни наличие магнитного момента у нейтральной частицы (например, у нейтрона), ни отрицательных магнитных моментов некоторых ядер. Тем не менее, изучение классического движения магнитного диполя в магнитном поле позволяет получить дополнительные (по сравнению с квантово-механическим рассмотрением) сведения о природе магнитного резонансного поглощения, особенно при рассмотрении нестационарных явлений. Недостатки классической модели указывают на сложность структуры ядра: полный угловой момент ядра получается в результате сложения в различных комбинациях орбитальных и спиновых движений частиц, входящих в состав ядра. Это сложение аналогично связи спиновых и орбитальных моментов электронов в атомах и молекулах.

Выражение 2.3 позволяет записать классическое уравнение движения магнитного момента 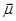 в векторной форме следующим образом:

                             d 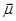/dt=g[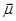 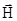],                                                              (2.4)

где 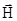 –напряженность внешнего магнитного поля.

Если в отсутствии магнитного поля вращать вектор 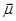с угловой скоростью 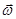, то, в соответствии с законом Ньютона для вращательного движения, выражение для d 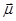/dt будет иметь вид:

                                   d 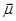/dt=[ 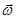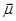].                                                          (2.5)

Из сопоставления выражений 2.4 и 2.5 следует, что действие магнитного поля 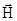 в точности эквивалентно вращению момента с угловой скоростью 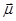=-g 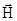 (2.6), т.е. ω=gH, или n=gH/2p (2.7), здесь n [Гц] ,H [Э] (уместно вспомнить, что [ab]=-[ba]).

Таким образом, в постоянном магнитном поле вектор магнитного момента будет прецессировать вокруг направления вектора 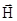 с постоянной угловой скоростью -g  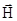независимо от направления вектора 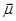, т.е. от угла между осью вращения частицы и направлением поля (рис.1).Угловой скоростью такой прецессии называют ларморовой частотой, а выражение 2.6 – формулой Лармора.

Если перейти к системе координат, вращающейся равномерно с угловой скоростью -g 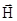, то при отсутствии других магнитных полей вектор магнитного момента  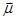 в этой системе координат будет оставаться неизменным по величине и направлению. Другими словами, во вращающейся системе координат постоянное магнитное поле как будто отсутствует.

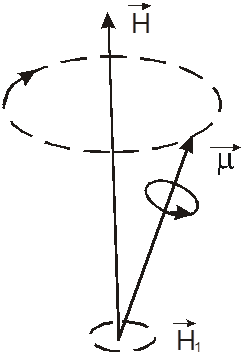
Рис.1. Прецессия магнитного момента в магнитном поле  

Допустим теперь, что кроме поля  введено другое, более слабое поле ₁, постоянное по величине и равномерно вращающееся в плоскости, перпендикулярной направлению  (рис.1). Если скорость вращения поля ₁ не равна частоте ларморовой  прецессии, то это поле будет вращаться и в упомянутой выше вращающейся системе координат. Наличие поля приводит к появлению момента сил [ 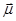₁], который стремится повернуть ядерный момент в плоскость, перпендикулярную . Если направление ₁ во вращающейся системе координат меняется, то направление соответствующего момента сил будет быстро меняться, и единственным результатом будут слабые периодические возмущения прецессии магнитного момента.

Если, однако, само поле ₁ вращается с ларморовой частотой, то во вращающейся системе координат оно будет вести себя подобно постоянному полю. Поэтому направление момента сил будет оставаться неизменным, что вызовет сильные колебания направления магнитного момента 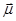, т.е. большие изменения угла между  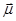и ₀. При изменении угловой скорости вращения поля ₁ колебания с наибольшей амплитудой возникают при совпадении этой скорости с ларморовой частотой. В этом случае говорят о явлении резонанса.

Аналогичное явление резонанса должно наблюдаться, когда направление поля ₁ фиксировано, а величина его меняется по синусоидальному закону с частотой, близкой к частоте ларморовой прецессии. Это происходит потому, что такое поле можно представить в виде суперпозиции двух равных полей, вращающихся с равными угловыми скоростями в противоположных направлениях (рис.2). При этом поле, вращающееся в направлении, противоположном направлению ларморовой прецессии, не будет оказывать влияния на резонанс.    

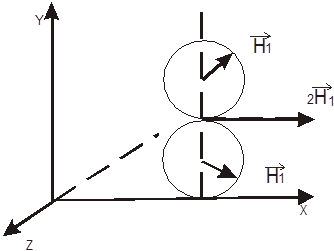
Рис.2. Разложение вектора магнитного поля  на два вектора, вращающиеся в противоположные стороны.

  На практике для создания магнитного поля, осциллирующего вдоль определенного направления, например, вдоль оси х, по катушке, ось которой перпендикулярна полю ₀ и направлена вдоль оси х, пропускают переменный ток. Напряжение с частотой w, приложенное к катушке, создает поле, эквивалентное двум вращающимся в противоположных направлениях полям величиной (Н₁cos wt+H₁sin wt) и (H₁cos wt – H₁sin wt).

Если w соответствует частоте резонанса, магнитный диполь поглощает энергию поля, создаваемого катушкой, вследствие чего вектор магнитного момента отклоняется в направлении к плоскости ху и во второй (приемной) катушке, расположенной вдоль оси у, наводится э.д.с.

Т.о., рассмотренная здесь классическая модель резонанса, объясняя суть явления, указывает и на экспериментальное его проявление, состоящее в непрерывном поглощении электромагнитной энергии поля Н₁.

2.2.Квантово-механическое рассмотрение условий резонанса.

При включении магнитного поля  каждое ядро приобретает дополнительную энергию -m , которую называют зеемановской. Гамильтониан в этом случае имеет очень простой вид

H=-m                                                                                                             (2.8)

Направляя ось z вдоль приложенного постоянного магнитного поля ₀, получаем

H=-gh ₀I_z                                                                                                                                                                   (2.9)

Собственные значения этого гамильтониана являются произведениями величины gh ₀ на собственные значения оператора I_z . поэтому возможные значения энергии равны

Е=-gh ₀m , m= I , I-1 , … , -I .                                                                (2.10)

Чаще всего для наблюдения магнитного резонанса применяют переменное магнитное поле, направленное перпендикулярно постоянному полю. Если амплитуду переменного поля обозначить через H⁰_x, то часть полного гамильтониана, приводящая к переходам, будет иметь вид

H_возм=-gh ⁰_xI_xcoswt                                                                                     (2.11)

Оператор I_xимеет отличные от нуля матричные элементы (m^’êI_x êm), связывающие состояния m и m^’, только в случае выполнения равенства m^’=m+\-1. В соответствии с этим разрешены переходы только между соседними уровнями, что дает

hw=DE=gh 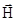₀                                                                                                                                                        (2.12)

или

w=g 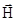₀                                                                                                           (2.13)

Это соотношение позволяет вычислить частоту, при которой можно наблюдать резонанс, если известно, каким образом можно определить g.

Вычислим магнитный и механический моменты частицы массой mи заряда e, движущейся по окружности радиуса r с периодом Т. В этом случае механический момент

J=mvr=m(2pr²/T),                                                                                         (2.14)

а магнитный момент

m=iA                                                                                                              (2.15)

(рассматриваем систему как контур тока i, охватывающий площадь А). Поскольку i= (e/c)(1/T), получаем

m=(е/c)(pr²/T).                                                                                               (2.16)

Сравнение вычисленных значений m и J дает g=m/J=e/2mc. Помимо оценки порядка величины g эта формула позволяет сделать вывод о том, что g для ядер должна быть на три порядка меньше величины g для электронов. Следует пользоваться самыми сильными магнитными полями, какие могут быть получены в лабораторных условиях, т.к. при этом возрастает величина поглощаемых квантов, и сигнал резонанса увеличивается.