Рассмотрим n – мерный интеграл

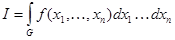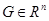 для .                                       (2)

Будем считать, что область интегрирования 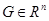, и что  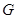ограниченное множество в 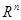. Следовательно, каждая точка х множества  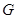имеет n координат: .

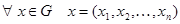Функцию 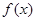 возьмем такую, что она ограничена сверху и снизу на множестве : .

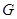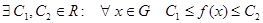Воспользуемся ограниченностью множества 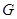 и впишем его в некоторый n – мерный параллелепипед 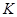, следующим образом:

,

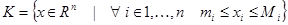где 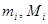- минимумы и максимумы, соответственно,  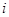- ой координаты всех точек множества : .

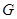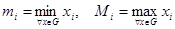Доопределяем подынтегральную функцию 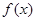 таким образом, чтобы она обращалась в ноль в точках параллелепипеда 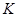, которые не принадлежат :

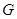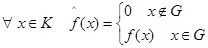                                                         (3)

Таким образом, уравнение (2) можно записать в виде

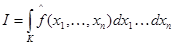.                                                              (4)

Область интегрирования представляет собой n – мерный параллелепипед 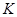 со сторонами параллельными осям координат. Данный параллелепипед можно однозначно задать двумя вершинами 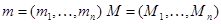, которые имеют самые младшие и самые старшие координаты всех точек параллелепипеда.

Обозначим через 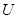 n-мерный вектор, имеющий равномерное распределение в параллелепипе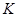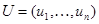де : , где .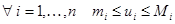

Тогда ее плотность вероятностей 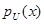 будет определена следующим образом

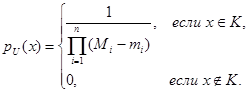                                                 (5)

Значение подынтегральной функции 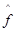 от случайного вектора  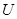будет случайной величиной 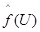, математическое ожидание  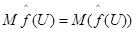которой является средним значением функции на множестве :

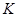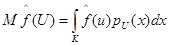.                                                                (6)

Среднее значение функции на множестве 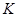 равняется отношению значения искомого интеграла к объему параллелепипеда :

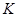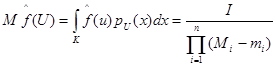                                           (7)

Обозначим 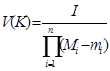 объем параллелепипеда .

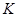Таким образом, значение искомого интеграла можно выразить как произведение математического ожидания функции и объема n- мерного параллелепипеда :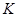

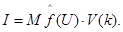                                                                          (8)

Следовательно, необходимо найти значение математического ожидания 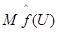. Его приближенное значение можно найти произведя n испытаний, получив, таким образом, выборку  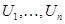случайных векторов, имеющих равномерное распределение на 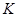. Обозначим  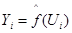и 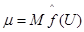. Для оценки математического ожидания воспользуемся результатом

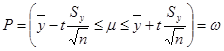,                                                    (9)

где ,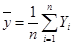

,

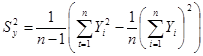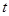 - квантиль нормального распределения, соответствующей доверительной вероятности .

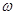Умножив двойное неравенство из (9) на 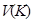 получим интервал для I:

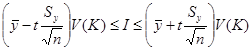.                                               (10)

Обозначим 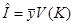 точечную оценку 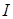. Получаем оценку (с надежностью ):

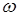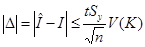.                                        (11)

Аналогично можно найти выражение для относительной погрешности :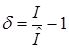

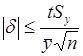.                                                (12)

Если задана целевая абсолютная погрешность 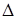, из (11) можно определить объем выборки, обеспечивающий заданную точность и надежность:

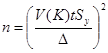.                                               (13)

Если задана целевая относительная погрешность, из (12) получаем аналогичное выражение для объема выборки:

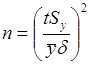.                                                            (14)

Сплайн – интерполяция.

В данном программном продукте реализована возможность задавать дополнительные ограничения области интегрирования двумя двумерными сплайн – поверхностями (для подынтегральной функции размерности 3). Для задания этих поверхностей используются двумерные сплайны типа гибкой пластинки \4\.

Под сплайном (от англ. spline - планка, рейка) обычно понимают агрегатную функцию, совпадающую с функциями более простой природы на каждом элементе разбиения своей области определения. Сплайн – функция имеет следующий вид:

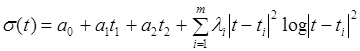.                         (15)

Исходные данные представляют собой 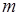 троек точек .

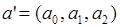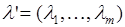Коэффициенты  и   определяются из системы:

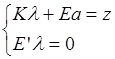,                                              (16)

где ,

.

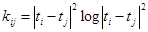
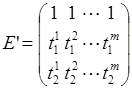Алгоритм расчета интеграла

Реализованный алгоритм включает следующие шаги:

1) выбирается начальное значение 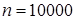, разыгрываются случайные векторы из  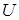и определяются  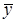и ;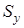

2) в зависимости от вида погрешности (абсолютная, относительная) определяется достигнутая погрешность; если она меньше целевой, вычисление прерывается;

3) по формулам (13) или (14) вычисляется новый объем выборки;

4) объем выборки увеличивается на 20%

5) переход к шагу 1;

6) конец.