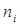Для того, чтобы найти решение уравнения равновесия 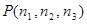, воспользуемся теоремой 1 из 1.7 из которой получим, что

,

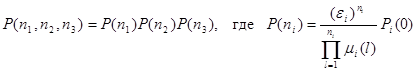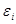-вероятность поступления заявок в i-ую подсистему.

Таким образом, нам необходимо найти 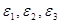. Для этого воспользуемся соотношением (3) из 1.7

Из системы 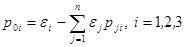 получим

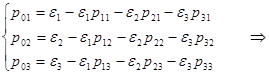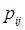 где -вероятности перехода

Матрица перехода имеет вид:

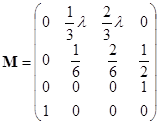
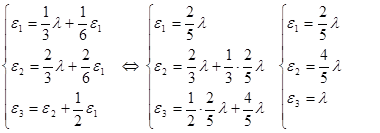
Тогда, получим

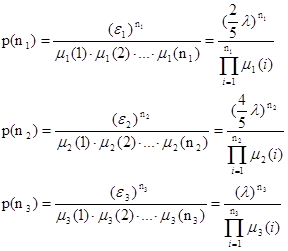
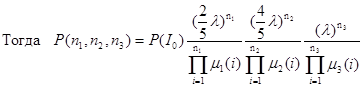
где Io - нулевой вектор.

Итак, стационарное распределение найдено с точностью до постоянного множителя P ( Io).

Условия эргодичности

Для исследования эргодичности применим эргодическую теорему Фостера (теорема 1 из 1.1)

Теорема (Эргодическая теорема Фостера).

Регулярная Марковская цепь с непрерывным временем и счетным числом состояний эргодична, если она неприводима и система уравнений

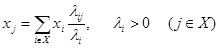
имеет нетривиальное решение 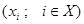 такое, что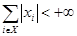

При этом существует единственное стационарное распределение, которое совпадает с эргодическим.

Рассмотрим условия этой теоремы.

Регулярность следует из того, что 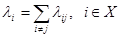. Неприводимость следует из того, что все состояния сообщаются с нулевым, то есть в любое состояние 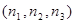можно перейти из нулевого (0,0,0) путем поступления, перехода, обслуживания заявок.

В качестве нетривиального решения системы уравнений из теоремы Фостера возьмем . Тогда для эргодичности потребуется, чтобы

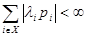
Тогда получим,

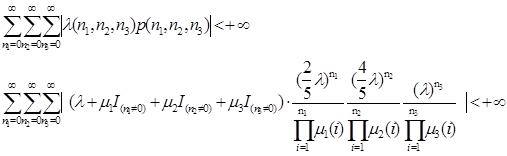
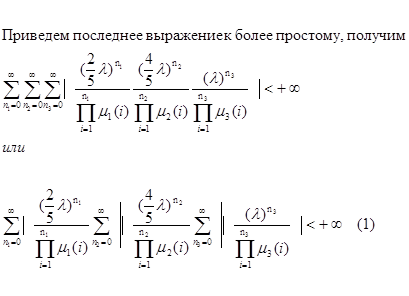
Условие (1) и есть искомое условие эргодичности. Если это условие будет выполнятся, то будет существовать единственное стационарное распределение, совпадающее с эргодическим.

Немарковский случай

Описание модели

Дана модель открытой сети массового обслуживания, точно такая как марковском случае Только предполагается, что длительность обслуживания отдельного требования распределена по произвольному закону. Пусть 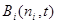 - произ. функция распределения времени обслуживания 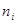-той заявки в 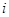-том узле, при этом предполагаем, что выполняется следующее требование:

.

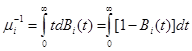Состояние сети в момент времени t определяется вектором

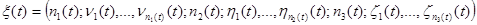, где

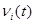 - остаточное время обслуживания заявки, первой подсистемой, стоящей в 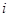-ой позиции.

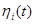 - остаточное время обслуживания заявки, второй подсистемой, стоящей в 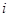-ой позиции.

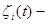 остаточное время обслуживания заявки, третьей подсистемой, стоящей в 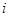-ой позиции.

Система LCFS PR.

Заявка, поступающая в 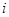-ый узел, вытесняет заявку с прибора и начинает обслуживаться. Вытесненная заявка идет в начало очереди.

 -

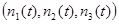не Марковский процесс.

Рассматривается следующий процесс

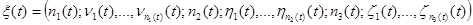
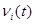 - остаточное время обслуживания заявки, первой подсистемой, стоящей в 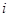-ой позиции.