Пусть входящий в открытую марковскую сеть массового обслуживания поток заявок описывается чистым процессом размножения с интенсивностью , причем в i-ую систему массового обслуживания входящая заявка поступает с вероятностью 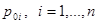 . Времена обслуживания заявок в i-той системе массового обслуживания распределены по показательному закону
. Времена обслуживания заявок в i-той системе массового обслуживания распределены по показательному закону 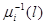 , зависящим от текущего числа заявок в i-той системе
, зависящим от текущего числа заявок в i-той системе  i=1,...,n.
i=1,...,n.
Дисциплины обслуживания заявок в системе сети FIFO. Переходы заявок между системами, а также уход заявки из сети описывается неприводимой цепью Маркова. Заявка, завершающая обслуживание в системе  , переходит с вероятностью
, переходит с вероятностью 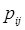 в систему
в систему 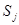 ,
, 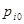 есть вероятность ухода заявки из i-ой системы массового обслуживания сети.
есть вероятность ухода заявки из i-ой системы массового обслуживания сети.
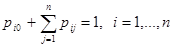
В этом случае многомерный процесс N (t), определяющий состояние сети, является многомерным аналогом процесса размножения и гибели. Предположим, что существует стационарное распределение
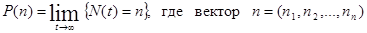 ,
,
принимает все возможные значения. Тогда, аналогично как и для одномерного процесса размножения и гибели, можно показать, что стационарное распределение единственно и удовлетворяет системе уравнений равновесия (баланса), которая представляет собой систему линейных разностных уравнений:
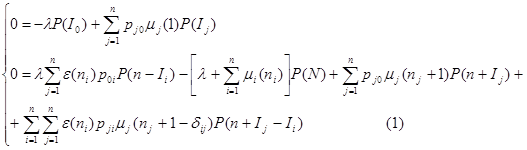
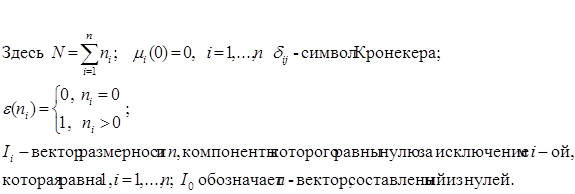
Для упрощения системы (1) введем величины 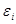 так, что
так, что 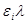 есть полная интенсивность поступления заявок в системы
есть полная интенсивность поступления заявок в системы 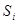 . Интенсивность
. Интенсивность 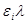 состоит из интенсивности потока заявок, поступающих извне
состоит из интенсивности потока заявок, поступающих извне 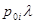 , и интенсивности поступления заявок в систему
, и интенсивности поступления заявок в систему 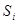 от других СМО, в том числе и от самой системы
от других СМО, в том числе и от самой системы 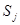 .
.
Поэтому 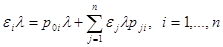 (2).
(2).
Из (2) получим 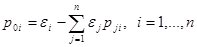 (3).
(3).
Соотношение (2) иногда называют законом сохранения потока заявок. Оно говорит о том, что интенсивность входящего потока заявок в i-тую СМО, i=1,..., n, в стационарном режиме равна интенсивности входящего потока заявок из этой системы.
Теорема1. (Джексона) Стационарное распределение может быть найдено в виде:
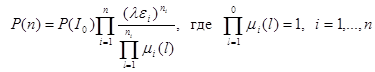
Нахождение решения для немарковского случая
Составив и решив систему дифференциально-разностных уравнений, найдется вид функции распределения
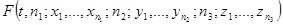
для случайного процесса 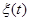 . Тогда можно найти
. Тогда можно найти 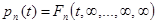 и
и 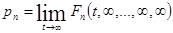 .
.
Так что нахождение функций
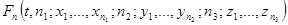
решит поставленную задачу.
Марковский случай
Описание модели



 1
1

Сеть массового обслуживания
Дана открытая марковская сеть массового обслуживания, состоящая из трех подсистем. Состояние сети в момент времени t определяется вектором

число заявок в i-ой подсистеме в момент времени t. Входящий поток является пуассоновским потоком с параметром 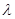 . Времена обслуживания заявок в i-ой системе массового обслуживания распределены по показательному закону с параметром
. Времена обслуживания заявок в i-ой системе массового обслуживания распределены по показательному закону с параметром 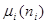 , зависящим от текущего числа заявок в i-ой системе, i=1,2,3.
, зависящим от текущего числа заявок в i-ой системе, i=1,2,3.
Заявки поступают из общего потока заявок во второй узел и первый узел с вероятностями  и
и  соответственно. После обслуживания во втором узле заявки поступают на третий узел. А после обслуживания на первом узле заявки поступают с вероятностью
соответственно. После обслуживания во втором узле заявки поступают на третий узел. А после обслуживания на первом узле заявки поступают с вероятностью 
 в третий узел либо с вероятностью
в третий узел либо с вероятностью 
 в первый узел, либо с вероятностью
в первый узел, либо с вероятностью  в третий узел. После обслуживания на 3 узле заявки уходят из системы.
в третий узел. После обслуживания на 3 узле заявки уходят из системы.
Уравнения равновесия
Предположим, что существует стационарное распределение 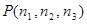 . Составим уравнение равновесия.
. Составим уравнение равновесия.
P 

 P
P 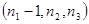
 +
+ 
 P
P 
 +
+
+ 
 P
P 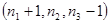
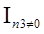 +
+  P
P 
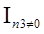 +
+
+ 
 P
P 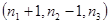
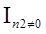 +
+ 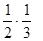
 P
P 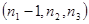
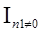 +
+
+ 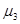 P
P 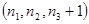
Дата: 2019-07-24, просмотров: 268.