Матричный метод решения системы уравнений (1) основан на непосредственном отыскании фундаментальной матрицы этой системы.
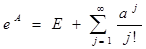 |
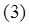 |
Экспонентой eA матрицы А называется сумма ряда
где Е – единичная матрица.
Свойство матричной экспоненты:
а) если АВ=ВА, то еА+В=еА*еВ= еВ *еА;
б) если А=S-1*B*S, то еА=S-1*eB*S, где матрица S – это матрица преобразования переменных из собственного базиса в базис исходных переменных.
в) матрица y(t)=eAt является решением матричной задачи Коши:
т.е. является фундаментальной матрицей системы (1).
Из свойства в) следует, что решение y(t) системы (1) удовлетворяющее условию y(0)=y0, определяется выражением y(t)=eAt*y0. Таким образом, задача нахождения решений системы уравнений (1) эквивалентна задачи отыскания матрицы eAt по матрице А.
Для вычисления матрицы eAt удобно представить матрицу А в виде:
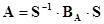 ,
,
где матрица S – это матрица преобразования переменных из собственного базиса в базис исходных переменных, а B А – жорданова форма матрицы А, т.к. eAt = S-1*eBt*S.
Жорданова форма матрицы зависит от вида характеристических чисел.
1. Пусть характеристические числа действительные кратные, тогда Жорданова форма матрицы размерности nxn имеет вид:
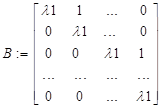
где 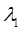 - действительный корень кратности n.
- действительный корень кратности n.
2. Если среди корней характеристического полинома имеются, как действительные разные, так и действительные кратные корни, то матрица В имеет вид:
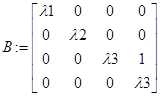
где 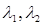 - действительные разные корни, а
- действительные разные корни, а 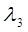 - действительный корень кратности 2.
- действительный корень кратности 2.
3. При наличии среди корней характеристического полинома корней комплексно-сопряженных Жорданова клетка выглядит следующим образом:
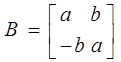
где а 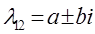 комплексно сопряженный корень характеристического полинома.
комплексно сопряженный корень характеристического полинома.
Так как в нашем случае среди характеристических чисел присутствуют, как комплексно-сопряженные корни л = 2 - ∨ л = 2 + , так и действительный разные корни л = -1 ∨ л = 1,то жорданова матрица выглядит следующим образом:
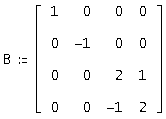
Из уравнения A*S = S*В, где S – невырожденная матрица, получаем систему 16-го порядка, из которой находим элементы матрицы S. Полученная матрица S будет выглядеть следующим образом:

Решаем систему 16-го порядка из уравнения A*S = S*В

Доопределяем некоторые элементы и получаем следующую матрицу S:

Сделаем проверку A*S - S*В=0:
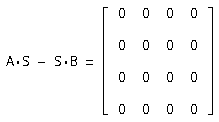
Значит матрица перехода найдена верно.
Для нахождения вектора решений y необходимо умножить матрицу S на 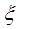 , где
, где 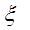 - это вектор, элементы которого зависят от корней характеристического многочлена:
- это вектор, элементы которого зависят от корней характеристического многочлена:
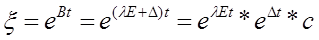
Для комплексных чисел 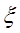 имеет следующий вид:
имеет следующий вид:
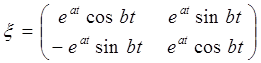
Для случая корней действительных разных:
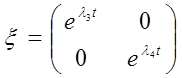
В нашем случае 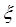 получается равной:
получается равной:
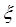 =
= 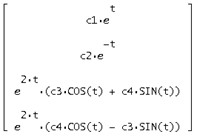
Отсюда найдем общее решение у=S* 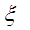 , получим:
, получим:
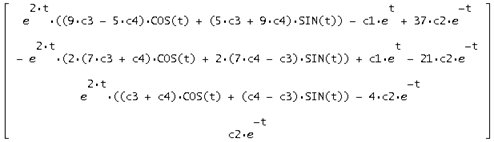
При подстановке решения в исходную систему получается верное равенство, из этого следует, что решение найдено верно:
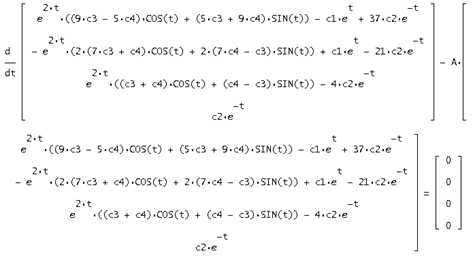
Дата: 2019-07-24, просмотров: 300.