Метод Эйлера заключается в следующем.

Решение системы (1) находится в виде:

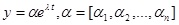 (5)

Функция (5) является решением системы (1), если 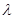 – собственное значение матрицы А, а а – собственный вектор этой матрицы, соответствующей числу 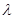. Если собственные значения 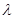₁, 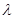₂, … , 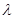_n матрицы А попарно различны и a₁, a₂, …, a_n соответствующие собственные векторы этой матрицы, то общее решение системы уравнений (1) определяется формулой :

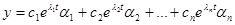
где С₁, С₂, … , С_n – произвольные числа.

Для случая кратных корней решение системы принимает вид

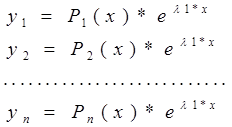 (6)

где Pi(x)-полиномы степени не выше, чем (к-1), имеющих в совокупности к произвольных коэффициентов. Так что среди коэффициентов этих полиномов к коэффициентов являются произвольными, а оставшиеся к·n-k выражаются через них. Для отыскания коэффициентов полиномов подставим решение (6) в исходную систему уравнений, приравняем коэффициенты при одинаковых функциях. Решим систему по отношению к (k·n-k) коэффициентов. Получим выражение всех коэффициентов через свободные.

Если для кратного собственного значения 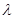 матрицы А имеется столько линейно независимых собственных векторов 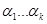, какова его кратность, то ему соответствует k независимых решений исходной системы:

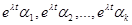
Если для собственного значения 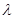 кратности k имеется только m (m<k) линейно независимых собственных векторов, то решения, соответствующие 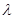, можно искать в виде произведения векторного многочлена степени k - m на 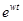, т.е. в виде:

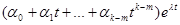
Чтобы найти векторы 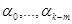, надо подставить выражение (4) в систему (3). Приравняв коэффициенты подобных членов в левой и правой частях системы, получим уравнение для нахождения векторов .

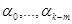Для данного задания были найдены следующие собственные значения:

.

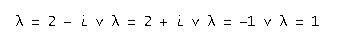Построили фундаментальную систему решений:

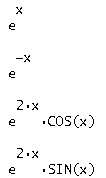
Найдем 1 строку фундаментальной матрицы решений для характеристического числа 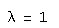. Запишем третью строку решений в общем виде:

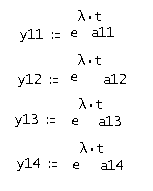
Где аij найдем по выражению:

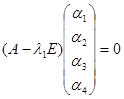 или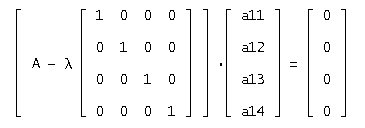

Полученная матрица:

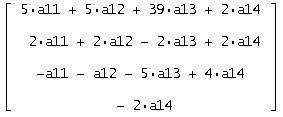
Решаем систему:

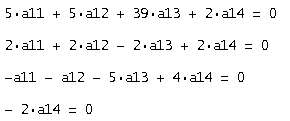
Полученные корни:

Доопределим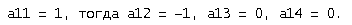

Тогда первая строка будет иметь вид:

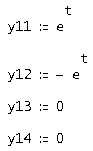
Аналогично найдем вторую строку фундаментальной матрицы решений для первого характеристического числа -1. Полученные значения:

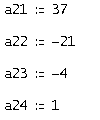
Тогда вторая строка будет иметь вид:

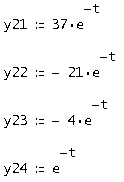
Найдем третью и четвертую строки фундаментальной матрицы решений для первого характеристического числа 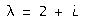. Сопряженный корень 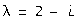не порождает новых вещественных линейно независимых частных решений.

Полученные значения:

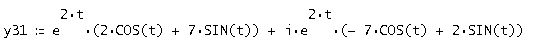
Отделяя в нем вещественные и мнимые части, получим два вещественных решения, которые и составляют первую и вторую строки фундаментальной матрицы решений

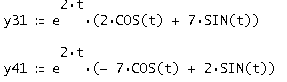
Аналогично остальные 3:

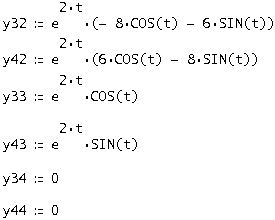
Запишем найденную фундаментальную матрицу решений:

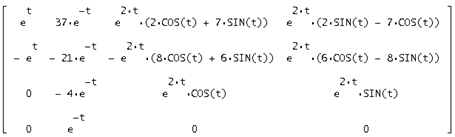
Умножим транспонированную фундаментальную матрицу решений на вектор свободных коэффициентов 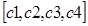и получим вектор общего решения исходной системы:

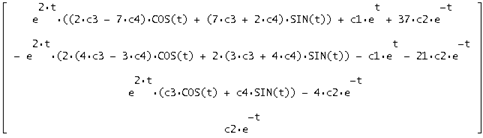
Сделаем проверку найденного решения следующим образом:

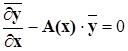
Получаем нулевую матрицу-столбец:

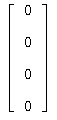что показывает, что общее решение найдено верно.