ЗМІСТ
ВСТУП
І ТЕОРЕТИЧНІ ОСНОВИ АНАЛІЗУ ВАРТОСТІ РИЗИКУ
1.1 Поняття про VАR-аналіз та методи його обчислення
1.2 Методи визначення VАR та їх застосування
ІІ ЗАСТОСУВАННЯ КОВАРІАЦІЙНОГО МЕТОДУ РОЗРАХУНКУ VAR НА ПРИКЛАДІ ФОНДОВОЇ БІРЖІ ПФТС
2.1 Методика розрахунку
2.2 Обчислення ризику на ринку акцій українських емітентів за даними ПФТС за 2006 р.
ІІІ МІЖНАРОДНИЙ ДОСВІД ЗАСТОСУВАННЯ VаR-АНАЛІЗУ
ВИСНОВКИ
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
ВСТУП
Актуальність теми дослідження. У цей час для терміна «Value-at-Risk» загальновживаного українськогоаналога немає, однак у періодиці найчастіше зустрічаються: «вартість, піддана ризику», «концепція інвестицій з врахуванням ризику», «ризикова вартість».
Вперше термін VaR (Value-at-risk) використали у 50-ті роки XX ст., коли він вперше був згаданий у рамках теорії портфеля Марковіца. Згодом VaR набув широкого використання у 90-х роках згідно з вимогами базельського комітету та зарекомендував себе як надійний помічник ризик-менеджерів. У 1996 р. Базельський комітет визначив чіткі вимоги щодо ринкових ризиків і дозволив найстійкішим у фінансовому плані банкам використовувати власні моделі оцінки і вимірювання ризиків (Value-at-Risk models), які дають змогу оцінити рівень ризиків кредитного та інвестиційного портфелів. Згодом значний внесок у розвиток ідеї використання VaR-методики зробили такі економісти, як Пірсон, Бассак, Шапіро, Мертон, Могран, Бедер та ін.
На сьогодні для оцінки і вимірювання кредитного ризику найбільші фінансові інститути світу використовують такі моделі методології VaR: Credit-Metrics, CreditRisk+, Portfolio Manager, CreditPortfolioView, Jarrow-Tumbull Model. Найпопулярнішою серед усіх перерахованих моделей стала методика вимірювання банківського кредитного ризику CreditMetrics, яка розробив у 1994 р. і вдосконалив у 1997 р. провідний оператор кредитного ринку - банк J.P. Morgan та його структурні підрозділі, який згодом став самостійною компанією, - Risk Metrics Group (RMG Corporation).
Українські банки лише починають на практиці застосовувати VaR-методики для оцінки ризику, що обумовлює потребу в нових наукових розробленнях щодо адаптації згаданих вище моделей до реалій української економіки та удосконаленні наявної методології обчислення основних показників кредитного ризику в умовах світової фінансової кризи.
Стан дослідження проблеми. Проблема застосування VaR-аналізу у сучасному фінансовому управління досить нова, однак існує достатньо розробок у цій галузі, включаючи часткові випадки і загальну методологію. Зокрема, загальними проблемами функціонування VaR займалися Альгін А. П., Бірман Г., Шмідт С., Камінський А. Б., Денисенко М.П., Домрачев В.М., Кононенко А. Ф., Холезов А. Д., Чумаков В. В. Часткові питання застосування VaR-аналізу у банківській сфері та кредитних процесах висвітлені у роботах Вітлинського В.В., Великоіваненко Г. І., Коломина М. Є., Лобанов А., Порох А., Сарана М. А., Верченко П. І. та ін. Серед зарубіжних авторів слід відзначити праці Gordy M., Haaf H., Reiss O., Schoenmakers J., Glasserman P.
Об’єкт дослідження – система методик визначення розміру ризику Value at risk в практиці фінансової діяльності.
Предмет дослідження - теоретичні і практичні проблеми застосування методики Value at risk в сучасному фінансовому аналізі ризиків.
Мета роботи - проаналізувати існуючу систему методик Value at risk, її особливості, принципи побудови, класифікаційні аспекти, методи застосування.
Для реалізації зазначеної мети були поставлені наступні завдання:
1) уточнити поняття про VАR-аналіз та методи його обчислення;
2) проаналізувати методи визначення VАR та їх застосування;
3) дослідити застосування коваріаційного методу розрахунку VAR на прикладі фондової біржі ПФТС;
4) вивчити міжнародний досвід застосування VАR-аналізу.
Методи дослідження. Під час вирішення визначених завдань використову-вались наступні методи дослідження: теоретичні: синтез, аналіз та узагальнення наукової літератури для теоретичного підгрунтя дослідження, метод порівняль-ного аналізу для порівняння різних джерел, метод порівняння та ін.
Структура роботи. Відповідно до мети та завдань дослідження визначено структуру роботи, яка складається зі вступу, трьох розділів, висновків і списку використаних джерел, загальний обсяг роботи склав 35 сторінок.
Рис.1. Типова функція Va R
По осі абсцис відкладені зміни цін ліквідації портфеля протягом певного періоду часу, по осі ординат - частота появи цих змін. Крива на малюнку задає щільність розподілу ймовірностей прибутків і втрат для даного портфеля і заданого періоду підтримки позицій. VaR-область відповідає обраному довірчому рівню 1-р = 98,5% у тому розумінні, що її площа становить 98,5% від загальної площі під кривою; відповідно площа області ліворуч становить 1,5% від загальної площі під кривою. Таким чином, VaR являє собою величину сумарних можливих втрат, які відповідають заданим довірчим рівням.
Резюмуючи все вищесказане по аналітичному методі, можна виділити основні позитивні й негативні сторони застосувань аналітичного методу для розрахунку VaR.
Його переваги:
1) простота й наочність розрахунків;
2) можливість розрахунку сукупної величини VaR для лінійних інструментів;
3) доступність методичних матеріалів.
Недоліки:
1) допущення про нормальний розподіл;
2) неможливість розрахунку VaR для нелінійних інструментів [4, c. 181].
Найвідомішою реалізацією аналітичного методу є система RiskMetrics, розроблена банком J. P. Morgan. Як основне допущення передбачається, що зміни ринкових факторів ризику мають нормальний розподіл. Це припущення дозволяє визначити розподіл прибутків і збитків для всього портфеля, який також буде нормальним. Потім, знаючи властивості закону нормального розподілу можна легко обчислити збиток, який буде траплятися не частіше заданого відсотка випадків, тобто показник ризикової вартості.
Наріжним каменем аналітичного методу є процедура відображення ризиків (англ. risk mapping). Вона припускає декомпозицію кожного інструмента з портфеля на безліч більше простих, стандартних інструментів або позицій, при цьому кожна стандартна позиція повинна відображати лише один ринковий фактор ризику. Для кожної стандартної позиції визначається її поточна вартість як функція від єдиних ринкових факторів, за умови, що значення інших ринкових факторів ризику є фіксованими. Для оцінки опціонів використовується лінійна апроксимація, при цьому вартість опціону виражається у вигляді дельта-еквівалентної позиції «спот».
Таким чином, вихідний портфель фінансових інструментів представляється у вигляді еквівалентного портфеля стандартних позицій. Еквівалентність, яка у загальному випадку може бути лише приблизною, означає, що портфель стандартних позицій має таку ж чутливість до змін значень ринкових факторів. Величина ризикової вартості визначається саме для еквівалентного портфеля стандартних позицій. Подібна апроксимація дає гарні результати, якщо число стандартних позицій досить великий і портфель не містить великої частки опціонів і заснованих на них інструментів, для оцінки яких лінійна апроксимація може виявитися неадекватною [15, c. 83].
На наступному етапі робиться припущення, що одноденні процентні зміни або збільшення логарифмів значень факторів ризику мають нормальний розподіл з математичним очікуванням, рівним нулю. Для кожного ринкового фактору проводиться статистична оцінка величини середнього квадратичного відхилення, а також розраховуються коефіцієнти кореляції між різними парами факторів. Отримані результати використаються для визначення середніх квадратичних відхилень і коефіцієнтів кореляції для вартостей стандартних позицій. Середнє квадратичне відхилення стандартної позиції розраховується як добуток середнього квадратичного відхилення відповідного ринкового фактору на коефіцієнт еластичності вартості позиції за даним ринковим фактором (процентна зміна вартості позиції при зміні величини ринкового фактору на 1%). Коефіцієнти кореляції для стандартних позицій дорівнюють коефіцієнтам кореляції між відповідними ринковими факторами за винятком того, що коефіцієнт кореляції міняє знак, якщо вартість стандартної позиції змінюється назад стосовно зміни ринкового фактору [15, c. 88].
Потім складається коваріаційна матриця змін вартостей стандартних позицій. За допомогою цієї матриці і формули дисперсії для суми нормально розподілених випадкових змінних можна розрахувати дисперсію вартості портфеля, яка складається зі стандартних позицій. Коваріаційна матриця множиться зліва і справа на вектор значень вартостей позицій, у результаті чого обчислюється значення дисперсії портфеля, звідки шляхом витягу квадратного кореня отримується його середнє квадратичне відхилення.
Нарешті, на основі властивостей нормального розподілу визначається значення ризикової вартості. Так, якщо довірчий інтервал заданий на рівні 95%, те величина ризикової вартості дорівнює 1,65 стандартного відхилення портфеля. Таким чином, величина ризикової вартості розраховується за наступною формулою:
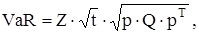
де Z - кількість середніх квадратических відхилень, яка відповідає заданому довірчому інтервалу; t - часовий обрій; p - вектор розміру позицій; Q - ковариационная матриця змін вартості позицій.
Метод історичного моделювання (historical simulation) є відносно простим підходом, який, на відміну від аналітичного методу, не опирається на теорію ймовірностей і вимагає відносно невеликого числа припущень щодо статистичних розподілів для ринкових факторів ризику. Як і в аналітичному методі, вартості інструментів портфеля повинні бути попередньо представлені як функції ринкових факторів ризику.
Шуканий розподіл прибутків і збитків отримується емпіричним шляхом. Поточний портфель піддається впливу реальних змін значень ринкових факторів ризику, які спостерігалися в минулому, наприклад, за останні n періодів. Для цього будується n безлічей гіпотетичних значень ринкових факторів на основі їхніх нинішніх значень і процентних змін за останні n періодів. Таким чином, отримані гіпотетичні значення грунтуються на реальних даних, але не тотожні їм. На основі цих гіпотетичних наборів значень ринкових факторів розраховується n гіпотетичних значень вартості портфеля. Порівняння цих значень з поточною вартістю портфеля дає можливість знайти n величин прибутків і збитків, викликаних зміною ринкових факторів. Отримані величини також є гіпотетичними, тому що портфель міг мати різний склад протягом останніх n періодів. Останнім етапом є побудова емпіричного розподілу ймовірностей прибутків і збитків, отриманих у результаті змін вартості портфеля, і визначення величини ризикової вартості [15, c. 90].
Метод статистичних випробувань Монте-Карло (Monte-Carlo simulation) також відноситься до методів імітаційного моделювання, і в чинність цього він має ряд загальних особливостей з методом історичного моделювання. Основна відмінність полягає в тому, що в методі Монте-Карло не проводиться моделювання з використанням реально спостережуваних значень ринкових факторів. Замість цього вибирається статистичний розподіл, який добре апроксимує зміни ринкових факторів, і проводиться оцінка його параметрів. Для цієї мети часто використається розподіл Стьюдента або суміш нормальних розподілів. Потім на основі обраного розподілу за допомогою генератора псевдовипадкових чисел генеруються тисячі або навіть десятки тисяч гіпотетичних наборів значень ринкових факторів. Отримані значення використовуються для розрахунку величин прибутків і збитків, викликаних зміною вартості портфеля. На останньому етапі будується розподіл прибутків і збитків портфеля й визначається величина ризикової вартості.
Вибір методу розрахунку показника ризикової вартості буде визначатися складом і структурою портфеля, доступністю статистичних даних і програмного забезпечення, обчислювальними потужностями й рядом інших факторів.
Аналітичний метод поступається методам імітаційного моделювання в надійності оцінки ризиків портфелів, які складаються з опціонів і заснованих на них інструментів, вартість яких залежить від ринкових факторів нелінійним образом, особливо на порівняно значних тимчасових горизонтах. Метод історичного моделювання концептуально простий і найбільш доступний для розуміння вищого керівництва, однак його реалізація вимагає наявності тимчасових рядів значень по всіх використовуваних у розрахунках ринкових факторах, що не завжди можливо для сильно диверсифікованих портфелів. Особливо це стосується даних по процентних ставках для валют країн, які не мають розвинених фінансових ринків. Крім того, історичне моделювання припускає, що поведінка ринку в минулому буде повторюватися і в майбутньому, що в загальному випадку невірно. Головними труднощами при реалізації методу Монте-Карло є вибір адекватного розподілу для кожного ринкового фактору й оцінка його параметрів. Крім того, оцінка ризиків великих диверсифікованих портфелів на основі методу Монте-Карло вимагає значних витрат часу й технічних ресурсів. Ще одна проблема полягає в тому, що гіпотетичні розподіли ймовірностей ринкових факторів, використовувані в аналітичному методі й методі Монте-Карло, можуть не відповідати реальності. Звичайно емпіричні розподіли змін ринкових факторів мають значний ексцес у порівнянні з нормальним розподілом, тобто випадки значних відхилень від середнього значення зустрічаються частіше, ніж це передбачено нормальним розподілом [4, c. 194].
Варто підкреслити, що керування ринковим ризиком не вичерпується наведеними вище процедурами. Зокрема, ризик-менеджер зобов'язаний звертати увагу на коректність обраної ним моделі ринку, на репрезентативність використовуваних даних і правильність статистичних гіпотез. Тому при керуванні ринковим ризиком дуже корисним представляється також апостеріорний аналіз. Наприклад, обчисливши VаR для заданого портфеля, необхідно потім простежити, чи дійсно перевищення втрат над цим VаR відбувається лише в заданому малому відсотку випадків. Невідповідність фактичного відсотка перевищень теоретичному повинне наводити на думку про корекцію моделі або процедур обчислення VаR. На терміновому ринку ММВБ подібні процедури аналізу фактичних ризиків застосовуються вже давно.
При управлінні ринковим ризиком не варто також забувати, що хоча межі застосування VаR досить широкі (наприклад, вже існують розробки по впровадженню концепції VаR у процес вимірювання кредитного ризику), він не є панацеєю від всіх лих. Зокрема, VаR не може захистити від ризиків, пов'язаних з коливаннями цін всередині періоду підтримки позицій (наприклад, протягом торговельної сесії). Крім того, застосування VаR обмежене при врахуванні рідкісних, але досить небезпечних подій (типу «чорного вівторка» або банківської кризи). У таких випадках поряд з VаR варто застосовувати й інші методи.
Методика розрахунку
Коваріаційний (variance-covariance) метод розрахунку величини VaR є єдиним інструментом, що дозволяє одержати оцінку VaR у замкнутому виді. В його основі лежить припущення про нормальний закон розподілу змін факторів ринкового ризику (щоденних доходностей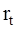 
) - цін фінансових інструментів, котирувань цінних паперів), що й дозволяє здійснювати моделювання цінового ризику.
Оскільки ціни активів та їх відношення не можуть бути від'ємними, то в якості доходності активу (rt) зазвичай приймаються логарифмічні прирощування значень цін [18, c. 143]:
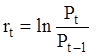, де
rt – доходність активу в період часу t;
Pt – ціна активу в період часу t;
Pt-1 – ціна активу в період часу t-1.
Якщо логарифми відношень цін (безперервно нарощена доходність) розподі-лені нормально, то ці відношення будуть відповідати логнормальному розподілу:
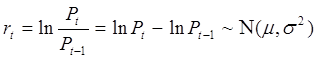, де
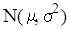- нормальний закон розподілу;
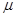- середнє значення доходності активу,
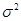- дисперсія доходності активу.
Досить часто на практиці замість логарифмічних прирощувань використаються звичайні процентні зміни цін, оскільки, як можна переконатися шляхом розкладання в ряд Тейлора, для незначних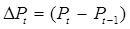 
ці величини будуть приблизно однаковими [18, c. 144]:
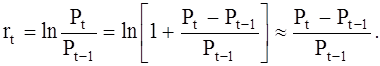
У випадку нормально розподіленої випадкової величини довірчий інтервал (1 -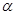 
) завжди характеризується єдиним параметром – квантілем 
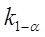, що показує положення певного значення випадкової величини (симетрично в обох хвостах розподілу) щодо середнього (E[rt] = 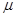), вираженого в кількості стандартних відхилень доходності портфелю ( 
).
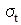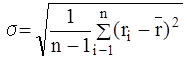, де
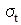- волатильність (мінливість) активу;
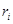- значення параметра доходності активу;
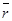- середня очікувана доходність;
n - кількість днів (спостережень).
Так, для найбільше часто застосовуваних значень довірчого інтервалу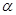 
в 95% й 99% відповідні квантілі будуть дорівнювати 1,65 й 2,33 (табличні дані) стандартних відхилень доходності портфелю.
На теоретичному рівні величина VaR в параметричному методі визначається формулою
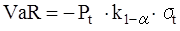
і відображає не ціну (або вартість) як таку, а її найбільш очікувану зміну за один день.
Досить часто знак «-» опускають й оперують абсолютним значенням.
Для часових горизонтів, що перевищують один день, припускають, що дисперсія змін цін пропорційна тривалості часового горизонту прогнозування, що дозволяє одержати оцінку ринкового ризику шляхом простого масштабування одноденної величини, тобто VaR в цьому випадку розраховується за формулою:
.
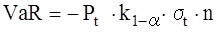Варто зазначити, що така оцінка буде прийнятною лише для порівняно невеликих інтервалів часу (не більше 10-15 днів), при цьому її точність падає зі збільшенням часового горизонту [18, c. 145].
Таким чином, центральною проблемою під час розрахунку величини VaR коваріаційним методом є знаходження дисперсії доходності фінансового інструменту.
За даними ПФТС за 2006 р.
На практиці варіаційно-коваріаційний метод розрахунку VaR має нижче наведений алгоритм.
На першому етапі визначається вихідний ряд показників (глибина розрахунку) - значень вартості певного портфелю для усіх фіксованих в історичному періоді станів ринку за 1-2 роки . У найпростішому випадку одного інструмента розглядається історичний ряд ринкових цін (котирувань), одержаних з показників ринкової статистики.
Як приклад застосування коваріаційного методу для оцінки ризиків на ринку акцій українських емітентів, за вихідний показник візьмемо індекс акцій ПФТС за 2006 рік (243 дні). Тобто, глибина розрахунку VaR складає 1 рік.
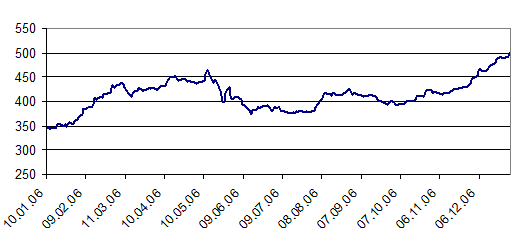
Рис. 1. Динаміка значень індексу ПФТС у 2006 р.
На другому етапі отриманий часовий ряд переводиться в ряд відносних змін за формулою:
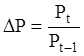
Наведеному вище ряду значень відповідають наступні відносні зміни індексу на рисунку 2.
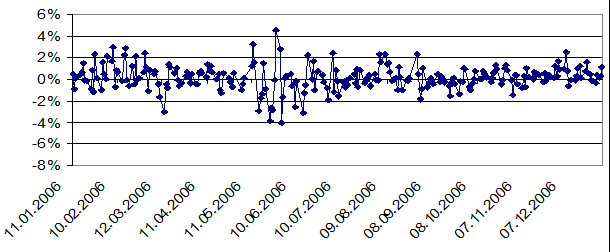
Рис. 2. Щоденні зміни значень індексу ПФТС у 2006 р.
Третім етапом, і першим специфічним кроком варіаційно-коваріаційного способу розрахунку VAR, є визначення параметрів розподілу, що найкращим чином наближають фактичний розподіл розглядуваного показника до нормального.
З точки зору статистики нормальний розподіл описується двома параметрами - математичним очікуванням і стандартним відхиленням - які для наведеного прикладу індекса ПФТС дорівнюють, відповідно, 0,16% й 1,15%.
Рисунок 3 ілюструє прийнятну точність наближення змін індексу ПФТС до нормального розподілу.
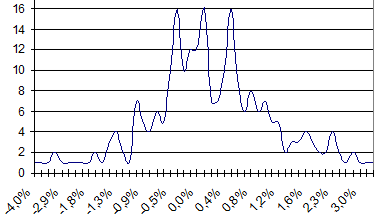
Рис. 3. Фактичний розподіл змін індексу ПФТС у 2006 р.
Далі визначається значення оберненого нормального розподілу відповідно до отриманих раніше параметрів:
– встановленим рівнем довіри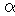 
- для короткої позиції, ризик для якої оцінюється по позитивних змінах, або
– оберненим довірчим рівнем (тобто 1 -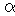 
) - для довгої позиції (для яких ризик проявляються лише в зниженні ринкової ціни) й, відповідно, негативних змінах.
Для даного прикладу індексу ПФТС найбільш типовим значенням довірчого рівня відповідають наступні значення оберненого нормального розподілу (таблиця 1).
Таблиця 1
Таблиця 2
ВИСНОВКИ
Відповідно до мети роботи та поставлених завдань дослідження можна зробити ряд узагальнючих висновків.
1. Однією з розповсюджених моделей оцінки ризиків є VaR модель. VaR - величина максимально можливих втрат, така, що втрати у вартості даного портфеля інвестора за певний період часу із заданою ймовірністю не перевищать цієї вели-чини. Таким чином, VaR дає імовірнісну оцінку потенційних збитків по портфелю протягом певного періоду при експертно заданому довірчому рівні. Існують три основних методи обчислення VAR: аналітичний (методом варіаіїи-коваріації), історичне моделювання і статистичне моделювання (метод Монте-Карло).
Основна ідея аналітичного методу полягає у виявленні ринкових факторів, які впливають на вартість портфеля, і апроксимації вартості портфеля на основі цих факторів. Перевага цього методу полягає в тому, що для більшості ринкових факторів всі необхідні параметри нормального розподілу добре відомі. Оцінка ризику в рамках методології VaR, отримана за допомогою аналітичного методу, збігається з оцінкою ризику, пропонованою сучасною портфельною теорією.
Метод історичного моделювання (historical simulation) є відносно простим підходом, який, на відміну від аналітичного методу, не опирається на теорію ймовірностей і вимагає відносно невеликого числа припущень щодо статистичних розподілів для ринкових факторів ризику.
Метод статистичних випробувань Монте-Карло (Monte-Carlo simulation) також відноситься до методів імітаційного моделювання, і в чинність цього він має ряд загальних особливостей з методом історичного моделювання. Основна відмінність полягає в тому, що в методі Монте-Карло не проводиться моделювання з використанням реально спостережуваних значень ринкових факторів, замість цього вибирається статистичний розподіл, який добре апроксимує зміни ринкових факторів, і проводиться оцінка його параметрів.
Загалом складно рекомендувати один з методів обчислення VaR. Вибираючи, якому з них віддати перевагу, необхідно враховувати макроекономічну ситуацію, а також мети й завдання конкретної організації. Як приклад опишемо застосування методології VaR при керуванні ризиками біржового термінового ринку.
2. Застосування методології VaR дозволяє в цілому вирішити завдання виміру ринкового ризику. Але крім того, що ринковий ризик необхідно правильно виміряти, необхідно також навчитися управляти ім. Керування ринковим ризиком являє собою дії по мінімізації ризику й захисту від нього. Керування ринковим ризиком повинне містити в собі наступні процедури:
1) вимір ринкового ризику для заданого портфеля (обчислення VaR);
2) рішення питання про прийнятність можливих втрат (у розмірі VaR);
3) можлива зміна портфеля з метою мінімізації його VaR (наприклад, хеджирование своїх позицій за допомогою термінових інструментів);
4) резервування капіталу в розмірі не меншому VaR для покриття можливих втрат.
3. Управління ринковим ризиком не вичерпується наведеними вище процеду-рами. Зокрема, ризик-менеджер зобов'язаний звертати увагу на коректність обраної ним моделі ринку, на репрезентативність використовуваних даних і правильність статистичних гіпотез. Тому при керуванні ринковим ризиком дуже корисним представляється також апостеріорний аналіз. Наприклад, обчисливши VаR для заданого портфеля, необхідно потім простежити, чи дійсно перевищення втрат над цим VаR відбувається лише в заданому малому відсотку випадків. Невідповідність фактичного відсотка перевищень теоретичному повинне наводити на думку про корекцію моделі або процедур обчислення VаR.
До недоліків також варто віднести те, що VaR вимагає проведення великої роботи зі збору історичних даних та їх обробки. Крім того, оцінка можливих змін вартості портфеля обмежена набором попередніх історичних змін. Типова проблема при використанні даного методу полягає у відсутності необхідного обсягу історичних даних. Щоб одержати більше точну оцінку VaR, необхідно використати якомога більший обсяг даних, але використання занадто старих даних приводить до того, що сьогоднішній (і тим більше майбутній) ризик буде оцінений на основі даних, які не відповідають поточному стану ринку.
4. В останні роки створення адекватної вартісної метрики ризику для різних видів орагнізацій стає однією з найбільш активно досліджуваних областей. Зокрема, сьогодні у світі для хеджування валютного ризику найчастіше використовують такий вид валютних деривативів, як форвардні валютні контракти. 59% всіх компаній хімічної промисловості, 52% металургійних компаній, 51% машинобудівних підприємств і 44% організацій, які займаються продажем товарів тривалого користування, використовують валютні форвардні контракти. До 42% автомобілебудівних компаній, підприємств харчової промисловості, транспортних компаній використовують валютні форварди.
Відповідно до VaR-рекомендацій Базельського комітету, позабалансові контракти повинні бути переведені в “балансовий інструмент” шляхом обчислення “кредитно-еквівалентної суми”, виробленого за допомогою додавання поточного ризику контракту і потенційного ризику контракту. Поточний ризик контракту визначається як вартість заміни контракту за існуючою ринковою ціною на момент обчислення кредитно-еквівалентної суми. Знаючи поточний ризик, можна відповістити на запитання: скільки буде коштувати заміна контракту за ринковою ціною, якщо контрагент відмовиться від виконання умов контакту сьогодні.
Крім того, методологія VаR стала особливо широко застосовуватися в останні роки й сьогодні використовується в якості єдиного уніфікованого підходу до оцінки ризику міжнародними банківськими і фінансовими організаціями. Наприклад, Банк міжнародних розрахунків (BIS) застосовує VаR як основу при встановленні нормативів величини власного капіталу щодо ризику активів.
Резюмуючи все вищесказане, можна сказати, що, у принципі, всі наведені моделі по управління інвестиційними ризиками є класикою інвестиційної оцінки ризиків. Насправді ж у світі використовується численна кількість моделей оцінки ризиків, кожна з яких має свої недоліки й переваги, які усуваються або доповнюються.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ:
1. Алєксєєв І.В., Захарчук О.В., Рим Н.Н. Банківський маркетинг. - Львів: Львівський банківський коледж Нац. банку України, 1998. - 96 с.
2. Альгин А.П. Грани экономического риска. - М.: Знание, 1991. - 64 с.
3. Бирман Г., Шмидт С. Экономический анализ инвестиционных проектов: Пер. с англ.- М: Банки и биржи, ЮНИТИ, 1997. - 631 с.
4. Вітлинський В.В., Великоіваненко Г. І. Ризикологія в економіці та підприємництві: Монографія. – К.: КНЕУ, 2004. – 480 с.
5. Вітлінський В.В. Актуальні проблеми ризикології. - К.: КДЕУ, 1996. Деп. в ДНТБ України. №Ук96. - 40 с.
6. Вітлінський В.В. Аналіз, оцінка і моделювання економічного ризику. - К.: ДЕМІУР, 1996. - 212 с.
7. Вітлінський В. В., Великоіваненко Г. І. Фінансовий ризик і методи його вимірювання // Фінанси України. - 2000. - № 5. - С. 13-23.
8. Денисенко М.П., Домрачев В.М. та ін. Кредитування та ризики: навч. посібник. - К. : Вид. дім «Професіонал», 2008. - 480 с.
9. Економічний ризик та методи його вимірювання: Посібник для студентів економічних спеціальностей вузів / А. Б. Камінський. - К.: ІМФ при Київському національному університеті імені Тараса Шевченка, 2002.
10. Коломина М.Е. Сущность и измерение инвестионных рисков // Финансы. - 1994. - № 4. - С. 19-26.
11. Кононенко А.Ф., Холезов А. Д., Чумаков В. В. Принятие решений в условиях неопределённости. - М.: ВЦ АН СССР, 1991. - 197 с.
12. Лобанов А. Проблема метода при расчете value at risk // Рынок ценных бумаг. 2000. №21. с. 54 – 58.
13. Лобанов А., Порох А. Анализ применимости различных моделей расчета value at risk на российском рынке акций // Рынок ценных бумаг. 2001. №2. - С. 65-70.
14. Лобанов А.А., Чугунов А.В. Энциклопедия финансового риск-менеджмента. – М.: Альпина Бизнес Букс, 2009. – 644 с.
15. Машина І.Н. Економічний ризик та методи його вимірювання. – Київ: Центр навчальної літератури, 2003. – 188 с.
16. Риски в современном бизнесе. /П. Г. Грабовый, С. Н. Петрова, С. И. Полтавцев и др. - М.: Аланс, 1994. - 200 с.
17. Сарана М.А., Верченко П.І. Неокласичний підхід до побудови оптимального портфеля цінних паперів // Проблеми економічного ризику: аналіз та управління. Збірних наукових праць за матеріалами Першої Всеукраїнської науково-практичної конференції (26-28 жовтня 1998 р.). - К.: Міносвіти України, КНЕУ, 1998. - С. 68-69.
18. Шора О.Є. Застосування VAR-методології в практичній діяльності комерційних банків // Облік і фінанси АПК. - 2005. - №12. - С. 142-145.
19. Ястремський О.І. Основи теорії економічного ризику. Навчальний посібник для студентів екон. спец. навч. закладів. - К.: «АртЕк», 1997. - 248 с.
20. Attikouris K. T., Attikouris K. G., Nakos K. (2003). Measuring repayment risk in shipping loans. FreightMetrics. Athens.
21. Danielsson J., DeVries C. (2000). Value-at-Risk and Extreme Returns. Annales d’economie at de statistique. No. 60.
22. Duffie D., Pan J. (1997). An overview of Value-at-Risk. The Journal of Derivatives, Spring.
23. Giot P., Laurent S. (2003). Value-at-Risk for long and short trading positions. Journal of Applied Econometrics. Vol.18, pp.641-664.
24. Gordy M. (2000). A Comparative Anatomy of Credit Risk Models. Journal of Banking and Finance, 24 (1-2). - Р. 119-149.
25. Gupton, G.M., Finger, C.C. and Bhatia, M. (1997). CreditMetrics - Technical Document, Morgan Guaranty Trust Co. - Доступний з: http://www.riskmetrics.com/ research/techdoc
26. Haaf H., Reiss O. and Schoenmakers J. (2003). Numerically stable computation of CreditRisk+. Technical report, Weierstrass-Institut. – 210 р.
27. Hull J., White A. (1998). Incorporating volatility updating into the historical simulation method for Value-at-Risk. Journal of Risk.
28. Manfredo M., Leuthold R. (2001). Market risk and cattle feeding margin: an application of Value-at-Risk. Agribusiness: an international journal. Vol. 17, No. 3. Summer.
29. Manganelli S., Engle R. (2001). Value at risk models in finance. Working paper No.75. European Central Bank Working paper series.
30. Paul Glasserman. Monte Carlo Methods in Financial Engineering. Springer, 2004. – 321 р.
31. web-сайт Першої фондової торговельної системи (ПФТС) www.pfts.com
32. Доклад «Модель оценки рисков VAR индивидуальных стратегий» // II Восточноевропейский риск-менеджмент форум 04.11.2003 // www.riskinfo.ru/analytics
ЗМІСТ
ВСТУП
І ТЕОРЕТИЧНІ ОСНОВИ АНАЛІЗУ ВАРТОСТІ РИЗИКУ
1.1 Поняття про VАR-аналіз та методи його обчислення
1.2 Методи визначення VАR та їх застосування
ІІ ЗАСТОСУВАННЯ КОВАРІАЦІЙНОГО МЕТОДУ РОЗРАХУНКУ VAR НА ПРИКЛАДІ ФОНДОВОЇ БІРЖІ ПФТС
2.1 Методика розрахунку
2.2 Обчислення ризику на ринку акцій українських емітентів за даними ПФТС за 2006 р.
ІІІ МІЖНАРОДНИЙ ДОСВІД ЗАСТОСУВАННЯ VаR-АНАЛІЗУ
ВИСНОВКИ
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
ВСТУП
Актуальність теми дослідження. У цей час для терміна «Value-at-Risk» загальновживаного українськогоаналога немає, однак у періодиці найчастіше зустрічаються: «вартість, піддана ризику», «концепція інвестицій з врахуванням ризику», «ризикова вартість».
Вперше термін VaR (Value-at-risk) використали у 50-ті роки XX ст., коли він вперше був згаданий у рамках теорії портфеля Марковіца. Згодом VaR набув широкого використання у 90-х роках згідно з вимогами базельського комітету та зарекомендував себе як надійний помічник ризик-менеджерів. У 1996 р. Базельський комітет визначив чіткі вимоги щодо ринкових ризиків і дозволив найстійкішим у фінансовому плані банкам використовувати власні моделі оцінки і вимірювання ризиків (Value-at-Risk models), які дають змогу оцінити рівень ризиків кредитного та інвестиційного портфелів. Згодом значний внесок у розвиток ідеї використання VaR-методики зробили такі економісти, як Пірсон, Бассак, Шапіро, Мертон, Могран, Бедер та ін.
На сьогодні для оцінки і вимірювання кредитного ризику найбільші фінансові інститути світу використовують такі моделі методології VaR: Credit-Metrics, CreditRisk+, Portfolio Manager, CreditPortfolioView, Jarrow-Tumbull Model. Найпопулярнішою серед усіх перерахованих моделей стала методика вимірювання банківського кредитного ризику CreditMetrics, яка розробив у 1994 р. і вдосконалив у 1997 р. провідний оператор кредитного ринку - банк J.P. Morgan та його структурні підрозділі, який згодом став самостійною компанією, - Risk Metrics Group (RMG Corporation).
Українські банки лише починають на практиці застосовувати VaR-методики для оцінки ризику, що обумовлює потребу в нових наукових розробленнях щодо адаптації згаданих вище моделей до реалій української економіки та удосконаленні наявної методології обчислення основних показників кредитного ризику в умовах світової фінансової кризи.
Стан дослідження проблеми. Проблема застосування VaR-аналізу у сучасному фінансовому управління досить нова, однак існує достатньо розробок у цій галузі, включаючи часткові випадки і загальну методологію. Зокрема, загальними проблемами функціонування VaR займалися Альгін А. П., Бірман Г., Шмідт С., Камінський А. Б., Денисенко М.П., Домрачев В.М., Кононенко А. Ф., Холезов А. Д., Чумаков В. В. Часткові питання застосування VaR-аналізу у банківській сфері та кредитних процесах висвітлені у роботах Вітлинського В.В., Великоіваненко Г. І., Коломина М. Є., Лобанов А., Порох А., Сарана М. А., Верченко П. І. та ін. Серед зарубіжних авторів слід відзначити праці Gordy M., Haaf H., Reiss O., Schoenmakers J., Glasserman P.
Об’єкт дослідження – система методик визначення розміру ризику Value at risk в практиці фінансової діяльності.
Предмет дослідження - теоретичні і практичні проблеми застосування методики Value at risk в сучасному фінансовому аналізі ризиків.
Мета роботи - проаналізувати існуючу систему методик Value at risk, її особливості, принципи побудови, класифікаційні аспекти, методи застосування.
Для реалізації зазначеної мети були поставлені наступні завдання:
1) уточнити поняття про VАR-аналіз та методи його обчислення;
2) проаналізувати методи визначення VАR та їх застосування;
3) дослідити застосування коваріаційного методу розрахунку VAR на прикладі фондової біржі ПФТС;
4) вивчити міжнародний досвід застосування VАR-аналізу.
Методи дослідження. Під час вирішення визначених завдань використову-вались наступні методи дослідження: теоретичні: синтез, аналіз та узагальнення наукової літератури для теоретичного підгрунтя дослідження, метод порівняль-ного аналізу для порівняння різних джерел, метод порівняння та ін.
Структура роботи. Відповідно до мети та завдань дослідження визначено структуру роботи, яка складається зі вступу, трьох розділів, висновків і списку використаних джерел, загальний обсяг роботи склав 35 сторінок.
І ТЕОРЕТИЧНІ ОСНОВИ АНАЛІЗУ ВАРТОСТІ РИЗИКУ
Дата: 2019-07-24, просмотров: 182.
