В экономических исследованиях издавна применялись простейшие математические методы. В хозяйственной жизни широко используются геометрические формулы. Так, площадь участка поля определяется путем перемножения длины на ширину или объем силосной траншеи - перемножением длины на среднюю ширину и глубину. Существует целый ряд формул и таблиц, облегчающих хозяйственным работникам определение тех или иных величин.[Кравченко 6].
В 60-е годы нашего столетия развернулась дискуссия о математических методах в экономике. Например, академик Немчинов выделял пять базовых методов исследования при планировании:
1) балансовый метод;
2) метод математического моделирования;
3) векторно-матричный метод;
4) метод экономико-математических множителей (оптимальных общественных оценок);
5) метод последовательного приближения.[немчинов].
В то же время академик Канторович выделял математические методы в четыре группы:
- макроэкономические модели, куда относил балансовый метод и модели спроса;
- модели взаимодействия экономических подразделений (на основе теории игр);
- линейное моделирование, включая ряд задач, немного отличающихся от классического линейного программирования;
- модели оптимизации, выходящие за пределы линейного моделирования (динамическое, нелинейное, целочисленное, и стохастическое программирование). [Контрович].
По широте применения различных методов в реальных процессах планирования несомненным лидером является метод линейной оптимизации, который был разработан академиком Канторовичем в 30-е годы ХХ-го века. Чаще всего задача линейного программирования применяется при моделировании организации производства. Вот как по Канторовичу выглядит математическая модель организации производства:
В производстве участвуют M различных производственных факторов (ингредиентов) - рабочая сила, сырье, материалы, оборудование, конечные и промежуточные продукты и др. Производство использует S технологических способов производства, причем для каждого из них заданы объемы производимых ингредиентов, рассчитанные на реализацию этого способа с единичной эффективностью, т.е. задан вектор ak = (a1k, a2k,..., amk ), k = 1,2...,S, в котором каждая из компонент aik указывает объем производства соответствующего ( i-го ) ингредиента, если она положительна; и объем его расходования, если она отрицательна ( в способе k ).
Выбор плана означает указание интенсивностей использования различных технологических способов, т.е. план определяется вектором x = (x1, x2,..., xS ) c неотрицательными компонентами [Контрович].
Обычно на количества выпускаемых и затрачиваемых ингредиентов накладываются ограничения: произвести нужно не менее, чем требуется, а затрачивать не больше, чем имеется. Такие ограничения записываются в виде
s
S a ikxk > bi ; i=1,2,...,m.
k=1
Если i > 0, то неравенство означает, что имеется потребность в ингредиенте в размере i, если i < 0,то неравенство означает, что имеется ресурс данного ингредиентов размере - i =¦ i¦. Далее предполагается, что использование каждого способа, связанного с расходом одного из перечисленных ингредиентов или особо выделенного ингредиента в количестве Ck при единичной интенсивности способа k. В качестве целевой функции принимается суммарный расход этого ингредиента в плане.
s
f(x) = S ckxk.
k=1
Теперь общая задача линейного программирования может быть представлена в математической форме. Для заданных чисел aik, ck, и bi найти
s
min S ckxk
k=1
при условиях
k > 0, k = 1,2,...,s [1]
s
S aikxk > bi, i = 1,2,...,m [2]
k=1
План, удовлетворяющий условиям [1] и [2], является допустимым, а если в нем, кроме того, достигается минимум целевой функции, то этот план оптимальный.
Задача линейного программирования двойственна, то есть, если прямая задача имеет решение, (вектор x =( x1, x2,..., xk)), то существует и имеет решение обратная задача основанная на транспонировании матрицы прямой задачи. Решением обратной задачи является вектор y = ( y1, y2... ,ym) компоненты которого можно рассматривать как объективно обусловленные оценки ресурсов, т.е. оценки, показывающие ценность ресурса и насколько полно он используется. [Контрович]
На основе объективно обусловленных оценок американским математиком Дж. Данцигом - был разработан симплекс-метод решения задач оптимального программирования. Этот метод весьма широко применяется. Алгоритм его весьма детально проработан, и даже составлены прикладные пакеты программ, которые применяются во многих отраслях планирования.
Его идея состоит в следующем: вначале достигается опорное решение поставленной задачи, т.е. допустимый вариант, удовлетворяющий всем ограничениям. Затем, проделывая ряд последовательных шагов, сводящихся к выполнению элементарных алгебраических преобразований, получают новое решение. Оно лучше или, по крайней мере, не хуже предшествующего. После конечного числа шагов (итераций) либо устанавливают неразрешимость задачи, либо опорный план является оптимальным.
Необходимо отметить, что симплекс метод работает только для системы линейных уравнений в каноническом виде, в которой должна быть предварительно записана исходная задача.
Решение задачи включает поиск опорного и нахождение оптимального решения. Признаки опорного решения – это наличие положительных свободных членов. В случае его отсутствия поступаем следующим образом:
1 – выбираем любой отрицательный свободный член;
2 – находим любой отрицательный коэффициент в строке отрицательного свободного члена;
3 – проводя деление коэффициентов столбца свободных членов на соответствующие коэффициенты столбца с выбранным отрицательным элементом, находим наименьшее положительное значение, которое укажет на разрешающий коэффициент.
После выбора разрешающего элемента симплексное преобразование выполняется по следующим правилам:
1. Новый коэффициент вместо разрешающегося равен 1, деленной на разрешающийся коэффициент. При этом новыми будут называться коэффициенты следующей симплексной таблицы по отношению к предыдущей;
2. Новые коэффициенты строки разрешающегося элемента равны предыдущим, деленным на разрешающий;
3. Новые коэффициенты столбца разрешающегося элемента равны предыдущим, деленным на разрешающий элемент, взятый с противоположным знаком;
4. Новые коэффициенты, не стоящие в строке или столбце разрешающегося элемента, равны частному от деления разности произведения коэффициентов главной и побочной диагоналей на разрешающий элемент.
Все результаты расчетов элементов заносятся в симплекс-таблицу. [Колеснев]
Несмотря на широту применения метода линейного программирования, он учитывает лишь три особенности экономических задач - большое количество переменных, ограниченность ресурсов и необходимость целевой функции. Конечно, многие задачи с другими особенностями можно свести к линейной оптимизации, но это не дает нам права упустить из виду другой хорошо разработанный метод математического моделирования - динамическое программирование. По сути, задача динамического программирования является описанием многошаговых процессов принятие решений. Задача динамического программирования можно сформулировать следующим образом :
имеется некоторое количество ресурса х, которое можно использовать N различными способами. Если обозначить через хi количество ресурса, используемое i-m способом, то каждому способу сопоставляется функция полезности (хi), выражающая доход от этого способа. Предполагается, что все доходы измеряются в одинаковых единицах и общий доход равен сумме доходов, полученных от использования каждого способа.
Теперь можно поставить задачу в математической форме. Найти
max y1(x1)+ y2(x2)+ ... + yn(xn)
(общий доход от использования ресурсов всеми способами) при условиях:
- выделяемые количества ресурсов неотрицательны;
[1] x1 > 0,..., xN > 0
- общее количество ресурсов равно x .
[2] x1 + x2 + ... + xN = x
Для этого общей задачи могут быть построены рекуррентные соотношения
¦1(x) = max {j1(x1)},
0 <=X1<= X
¦k(x) = max {jk(xk)+ ¦k-1(x - xk)}.
к = 2,3,..., N,
с помощью которых находится ее решение.
При выводе этих рекуррентных соотношений, по сути, использовался следующий принцип, оптимальная стратегия обладает тем свойством, что по отношению к любому первоначальному состоянию после некоторого этапа решения совокупность последующих решений должна составлять оптимальную стратегию. Этот принцип оптимальности лежит в основе всей концепции динамического программирования. Именно благодаря ему удается при последующих переходах испытывать не все возможные варианты, а лишь оптимальные выходы. Рекуррентные соотношения позволяют заменить чрезвычайно-трудоемкие вычисления максимума по N переменным в исходной задаче решением N задач, в каждой из которых максимум находится лишь по одной переменной.
Таким образом, метод динамического программирования позволяет учесть такую важную особенность экономических задач, как детерминированность более поздних решений от более ранних. [беллман]
Кроме этих двух, достаточно детально разработанных методов, в экономических исследованиях в последнее время стали применяться множество других методов.
Одним из подходов к решению экономических задач является подход, основанный на применении новой математической дисциплины - теории игр.
Суть этой теории заключается в том, что игрок (участник экономических взаимоотношений) должен выбрать оптимальную стратегию в зависимости от того, какими он представляет действия противников (конкурентов, факторов внешней среды и т.д.). В зависимости от того, насколько игрок осведомлен о возможных действиях противников, игры (а под игрой здесь понимается совокупность правил, тогда сам процесс игры это партия) бывают открытые и закрытые. При открытой игре оптимальной стратегией будет выбор максимального минимума выигрыша ("максимина") из всей совокупности решений, представленных в матричной форме. Соответственно противник будет стремится проиграть лишь минимальный максимум ("минимаск") который в случае игр с нулевой суммой будет равен "максимину". В экономике же чаще встречаются игры с ненулевой суммой, когда выигрывают оба игрока.
Кроме этого в реальной жизни число игроков редко бывает равно всего двум. При большем же числе игроков появляются возможности для кооперативной игры, когда игроки до начала игры могут образовывать коалиции и соответственно влиять на ход игры. [нейман]
Создатель теории игр Дж. Нейман еще в 1947 г. установил, что любую конечную игру двух лиц с нулевой суммой можно представить в виде задачи линейного программирования и наоборот. Для изучения данного подхода обозначим через Р1, Р2 …Рm вероятность применения игроком А в ходе игры своих чистых стратегий А1, А2 …Аm. Тогда пусть Q1, Q2 …Qn – вероятности применения игроком В своих чистых стратегий В1, В2 …Вn .
Для вероятностей Pi и Qj выполняются условия:
m
Pi ≥ 0, i=1, m(i=1, 2 … m).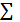 
Pi = 1,
i=1
n
Qj ≥ 0, j = 1 n(j=1,2,…n) 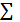Qj =1
j=1
если обозначим смешанные стратегии первого (А) и второго (В) игроков через Q и P, то Q=( Q1, Q2 …Qn), P=( Р1, Р2 …Рm). Например смешанной стратегией игрока А является полный набор вероятностей применения его чистых стратегий. [Колеснев]
Методы управления запасами. В научных исследованиях аграрной экономики особое внимание уделяется такому аспекту повышения эффективности работы предприятий, как грамотное управление имеющимися запасами. Во всех сферах АПК важно поддерживать рациональный уровень запасов (сырья, полуфабрикатов, готовых изделий). Затраты на хранение слишком больших запасов уменьшают прибыльность организации; подержание запасов на слишком низком уровне связано с риском возникновения дефицита и остановкой производства. Для компромиссного решения данной проблемы применяют модели управления запасами.
Запас – это все то, на что имеется спрос и что выключено временно из потребления. В народном хозяйстве различают: а) запасы средств производства; б) запасы предметов потребления. Если рассматривать совокупные запасы на пути технологической цепи «поставщик – потребитель», то их можно разделить на две основные части: товарные и производственные.
Товарные – это часть совокупных запасов, которые находятся в сфере обращения. Они формируются в различных звеньях оптовой и розничной торговли, на складах предприятий-изготовителей, на снабженческих и сбытовых базах.
К производственным относится часть совокупных запасов, находящаяся в руках производителей и вступившая (или готовая вступить) в процесс непосредственного производства. Под ними подразумевается продукция производственно-технического назначения.
В процессе применения методов управления запасами важно понимать и учитывать приведенные ниже особенности.
1. Величина запаса. Она определяется в натуральном или стоимостном выражении. В натуральных величинах (т, кг, шт) измеряется запас отдельного товара, сырья, инструмента или их родственной группы. Совокупный запас измеряется в стоимостном выражении.
2. Спрос- потребность в материальных ресурсах или товарах. Он бывает детерминированным (достоверно известный, характеризуемый заранее определенной величиной) или недетерминированный (случайный, стохастический, описанный вероятностным распределением), что приводит к постановке детерминированных и стохастических моделей.
В свою очередь, детерминированный спрос может быть:
- статический (стационарный, постоянный во времени)
- динамический (нестационарный, когда объем спроса является функцией времени).
3. Порядок пополнения запасов (или срок выполнения заказа). Речь идет об интервале времени между моментом размещения заказа и его поставкой.
4. Издержки. Цель модели управления запасами – сведение к минимуму отрицательных последствий накопления запасов, что выражается в определённых издержках. Эти издержки бывают трех основных видов: на размещение заказов, на хранение, а также потери, связанные с недостаточным уровнем запасов. В этом случае продажа готовой продукции или предоставление обслуживания становятся невозможными, а также возникают потери от простоя производственных линий, в частности, в связи с необходимостью оплаты труда работников, хотя они не работают в данный момент.
Поддержание высокого уровня запасов избавляет от потерь, обуславливаемых их нехваткой. Закупка в больших количествах материалов, необходимых для создания запасов, во многих случаях сводит к минимуму издержки на размещение заказов, поскольку предприятие может получить соответствующие скидки и снизить объем «бумажной работы». Однако эти потенциальные выгоды перекрываются дополнительными издержками типа расходов на хранение, перегрузку, выплату процентов, затрат на страхование, потерь от порчи, воровства и т.д
Имитационное моделирование. Имитационное моделирование обозначает процесс создания модели и ее экспериментальное применение для определения изменений реальной ситуации. Главная идея имитационного моделирования состоит в использовании некоего устройства для имитации реальной системы для того, чтобы исследовать и понять ее свойства, поведения и характеристики. Специалисты по производству и финансам могут разрабатывать модели, позволяющие имитировать ожидаемый прирост производительности и прибыли в результате применения новой технологии или изменения состава рабочей силы.
Имитация используется в ситуациях, слишком сложных для математических методов типа линейного программирования. Это может быть связано с чрезмерно большим числом переменных, трудностью математического анализа определенных зависимостей между переменными или высоким уровнем неопределенности.
Имитационные методы применяются в различных сферах АПК.
1. Можно смоделировать различные параметры, связанные с производственной, коммерческой и внешнеторговой деятельностью организаций. (количество выпускаемой продукции, объем продаж, ценовые характеристики, урожайность сельскохозяйственных культур, текучесть кадров и др.)
2. Можно решить экономические задачи производственно-технологического характера, возникающие при управлении запасами и в процессе создания систем массового обслуживания.
Использование методов имитационного моделирования приносит исследователю ряд преимуществ, так как:
1. обеспечивает учет неопределенности различных переменных (например, цены конкурентов, сроки поставки и д.);
2. позволяет проводить сравнение альтернативных вариантов (например, можно проанализировать воздействие различной политики ценообразования на спрос или системы налогообложения на рост производства);
3. дает возможность оценивать многообразные исходы;
4. устраняет риски, так как позволяет не проверять различные стратегии в реальных ситуациях;
5. ведет к экономии финансовых средств и времени.
В некоторых задачах имитационное моделирование может проводиться путем формального описания реальной последовательности взаимосвязей между показателями, не используя специального математического аппарата. В этом суть сингулярной имитационной модели, которая предназначена для машинной имитации исследуемого экономического процесса путем изменения входных данных.
Имитационне модели, в которых присутствует фактор времени, различают двух типов:
1. Непрерывные модели используются для систем, поведение которых изменяется непрерывно во времени. Типичным примером непрерывной имитационной модели является изучение динамики населения
2. Дискретные модели используются для систем, поведение которых изменяется лишь в заданные моменты времени.
Методы имитационного моделирования также используются для решения задач, связанных с массовым обслуживанием. Такие ситуации возникают там, где есть покупатели, а также товары или заказы, поступающие в определенное время. При этом обслуживание осуществляется в определенной последовательности.
Итак, имитационное моделирование – это часто весьма практичный способ подстановки модели на место реальной системы или натурального прототипа. Эксперименты на реальных или прототипных системах стоят дорого и продолжаются долго, а релевантные переменные не всегда поддаются регулированию. Экспериментируя на модели системы, можно установить, как она будет реагировать на определенные изменения или события, в то время когда отсутствует возможность наблюдать эту систему в реальности. Если результаты экспериментирования с использованием имитационной модели свидетельствует о том, что модификация ведет к улучшению, руководитель может с большей уверенностью принимать решение об осуществлении изменения в реальной системе.
Дата: 2019-07-24, просмотров: 227.
