Обтекаемый током i прямолинейный проводник длиной l (рис. 1), расположенный в магнитном поле с индукцией В, испытывает механическую силу

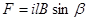                                                                          (1)

где β- угол между направлением вектора магнитной индукции и направлением тока в проводнике.

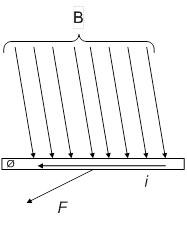
Рис. 1.

Для системы из нескольких обтекаемых током проводников можно всегда представить, что любой из этих проводников расположен в магнитном поле, созданном токами других проводников, и соответствующим образом взаимодействует с этим полем, т. е. между проводниками, охваченными общим магнитным потоком, всегда возникают механические силы. Эти силы называются электродинамическими.

Аналогичные силы возникают между проводником, обтекаемым током, и ферромагнитной массой.

Направление действия силы

Направление действия силы определяется «правилом левой руки».

Направление действия силы может быть также определено из следующего общего положения: силы, действующие в контуре с током, стремятся изменить конфигурацию контура так, чтобы охватываемый контуром магнитный поток увеличился.

Удобным для определения направления действия электродинамической силы является метод, предложенный академиком В.Ф. Миткевичем, основанный на представлении бокового распора и тяжения магнитных линий.

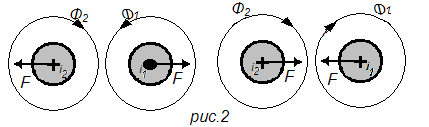
Рисуют и накладывают друг на друга картины магнитных полей, создаваемых током каждого из проводников. Благодаря боковому распору магнитных силовых линий сила, действующая на проводник, направлена в сторону, где поле ослаблено (рис. 2).

Методы расчета электродинамических сил

Расчет электродинамических сил ведется обычно либо на основании закона взаимодействия проводника с током и магнитным полем (первый метод), либо по изменению запаса магнитной энергии системы (второй метод).

Первый метод

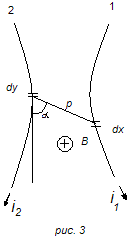
Расчет электродинамических сил на основании закона взаимодействия проводника с током и магнитным полем. Возьмем систему из двух произвольно расположенных проводников 1 и 2 (рис. 3), обтекаемых токами i ₁ и i ₂ . Напряженность магнитного поля, создаваемого элементом dy проводника 2 в месте расположения элемента dx проводника 1, будет

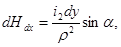                        (2)

где α — угол между вектором ρ и направлением тока по элементу dy .

Весь проводник 2 создает в месте расположения элемента dx напряженность магнитного поля

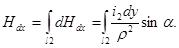            (3)

Элементарная сила, действующая на элемент dx, обтекаемый током i₁

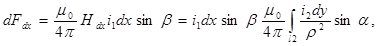               (4)

где ρ — угол между вектором магнитной индукции В = μ₀ H_dx и вектором тока i ₁;

μ₀ ^— магнитная проницаемость воздуха.

Полную силу F взаимодействия между проводниками 1 и 2 получим после интегрирования dF_dx по всей длине проводника 1:

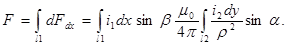                                  (5)

Считая токи i ₁ и i ₂ неизменными по всей длине проводника, уравнение (5) можно переписать в виде произведения членов:

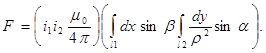                                      (6)

Первый член этого выражения зависит только от значений токов. Второй член зависит только от взаимного геометрического расположения проводников и представляет собой безразмерную величину. Эту величину часто называют коэффициентом контура, который обозначим буквой с. Тогда

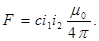                                                                       (7)

т.е. сила взаимодействия между двумя проводниками, обтекаемыми токами i ₁ и i₂, пропорциональна произведению этих токов (квадрату тока при i ₁ = i ₂) и зависит от геометрии проводников.

Подставив в уравнение (7) значение μ₀ = 4π10^-7 и вычисляя силу в ньютонах, получим

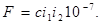                                                                       (8)

Второй метод

Расчет электродинамических сил по изменению запаса электромагнитной энергии контуров. Электромагнитное поле вокруг проводников и контуров с током обладает определенным запасом энергии. Электромагнитная энергия контура, обтекаемого током i ,

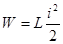                                                                               (9)

Электромагнитная энергия двух контуров, обтекаемых токами i ₁ и i ₂ ,

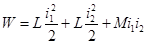                                                              (10)

где L ₁ , L ₂ — индуктивности контуров; М — взаимная индуктивность контуров.

Всякая деформация контура (изменение расположения отдельных его элементов или частей) или изменение взаиморасположения контуров приводят к изменению запаса электромагнитной энергии. При этом работа сил в любой системе равна изменению запаса энергии этой системы:

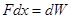                                                                             (11)

здесь dW — изменение запаса энергии системы при деформации системы в направлении х под действием силы F .

На указанном законе (11) и основан второй метод определения электродинамических сил в контурах. Электродинамическая сила в контуре или между контурами, действующая в направлении х, равна скорости изменения запаса энергии системы при деформации ее в том же направлении:

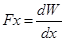                                                                              (12)

Согласно сказанному электродинамическая сила в контуре, обтекаемом током i ,

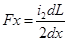                                                                              (13)

а электродинамическая сила между двумя взаимосвязанными контурами с токами i₁ и i₂ будет

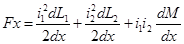                                                      (14)