Адресный интервал - это непрерывный ряд двоичных N-битных номеров, которые можно представить двумя номерами: минимальным и максимальным. Допустим, что узел в k каскаде получает ячейку, заголовок которой содержит адресный интервал, состоящий из двух бинарных номеров min(k-1)=m₁...m_N и max(k-1)=M₁...M_N, где k-1 обозначает каскад, из которого ячейка прибыла в k каскад. По обобщенному алгоритму самотрассировки маршрут ячейки определяется так (рисунок 4.3) [14]:

1. если m_k=М_k=0 или m_k=М_k=1, тогда отправьте ячейку в выводы 0 или 1 соответственно.

2. Если m_k=0 и М_k=1, тогда копируйте ячейку, модифицируйте заголовки обеих копий (по ниже данной схеме) и отправьте копии в соответствующий канал.

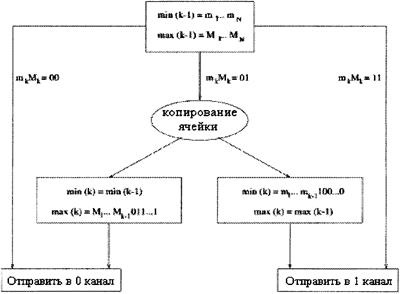
Рисунок 4.3 - Логическая схема коммутационного узла в k каскаде широкополосной Баньян сети

Модификация заголовка ячейки заключается в делении исходного адресного интервала на два подинтервала, что выражается в следующей рекурсии: для ячейки, отправленной в канал 0

min(k)=min (k-1)=sm₁...m_N,

max(k)=M₁.....M_k-101....1,

И для ячейки, отправленной в канал 1

min(k)=m₁....m_k-1 10....0,

max(k)=max(k-1)=M₁.....М_N

На рисунке 4.4 (а) представлена схема алгоритма логического деления интервалов. Из правил ясно, что m_i=M_i, i=1...k-1 действительно для каждой прибывающей в каскад k ячейки. Событие m_k=1 и M_k=0 исключено.

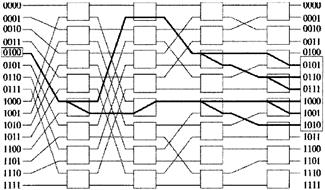
Рисунок 4.4 (а) - Схема алгоритма логического деления интервалов

На рисунке 4.4 (b) представлено дерево, которое образуется при копировании ячеек в соответствии с их адресными интервалами [12,14].

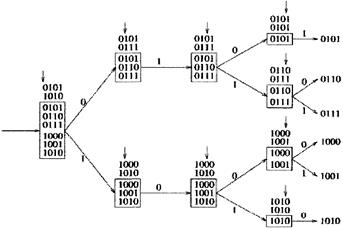
Рисунок 4.4 (b) - Дерево, образованное при копировании ячеек в соответствии с их адресными интервалами

УСЛОВИЯ НЕ БЛОКИРОВАНИЯ В ШИРОКОПОЛОСНЫХ БАНЬЯН СЕТЯХ

Широкополосная Баньян сеть является не блокирующей, если активные входы х₁…x_k и соответствующие выходы Y₁...Y_k соответствуют следующим требованиям [13,18]:

- Монотонность Y₁<Y₂ <....<Y_k или Y₁>Y₂>...>Y_k

- Концентрация: любой ввод между двумя активными вводами так же является активным.

Неравенство Y_i<Y_J означает, что каждый адрес выхода в Y_J меньше адреса выхода в Y_J. На рисунке 4.5 дан пример неблокирования с активными вводами x₁=7, х₂=8, х₃=9 и соответствующими выходами Y₁={1,3}, Y₁= {4,5,6}, Y3={7,8,10,13,14}.

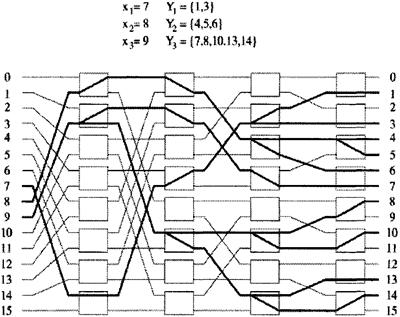
Рисунок 4.5 - Условия не блокирования в широкополосной Баньян сети

ПРОЦЕСС КОДИРОВАНИЯ

Схема сумматора (RAN), совместно с шифратором адресов (DAE), используется для организации адресов назначения каждой ячейки таким образом, чтобы каждая существенная ячейка была копирована без конфликтов в широкопосной Баньян сети. В ней проходят два процесса копирования ячеек: процесс кодирования и процесс декодирования. В процессе кодирования осуществляется преобразование рядов номеров копий, указанных в заголовках входящих ячеек, в ряд монотонных адресных интервалов, образующих заголовки ячеек в широполосной Баньян сети. Этот процесс осуществляется схемой сумматора и рядом шифраторов фиктивных номеров. От процесса декодирования зависит адрес назначения копий с транслятора номеров канала (TNT) [12,14].

Рекурсивная структура log₂N схемы сумматора показана на рисунке 4.6.

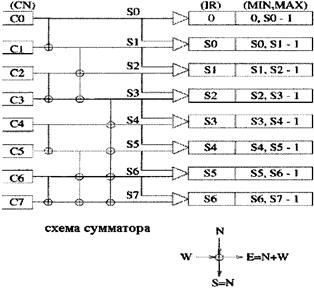
Рисунок 4.6 - Схема сумматора и шифратора фиктивных адресов

Схема сумматора состоит из (N/2)log₂N сумматоров, каждый с двумя вводами и выводами. Вертикальная линия обозначает пересылку. Восточный ввод равен сумме западного и северного вводов, а южный вывод продолжает северный ввод. Текущие суммы CN генерируются у каждого порта в конце log₂N каскадов, а затем шифраторы фиктивных адресов образуют новые заголовки из соседних текущих сумм. Новый заголовок содержит два поля: интервал фиктивных адресов, представленный двумя 1оg₂N-битовыми двоичными номерами (минимальным и максимальным). Другое поле содержит индексный эталон, равный минимуму адресного интервала. Заметьте, что длина каждого интервала равна соответствующему номеру копии в обоих адресных схемах. Примем за S_i i-текущую сумму. Тогда последовательность интервалов фиктивных адресов производится так [18]:

(0,S₀-1),(S₀,S₁)……..(S_N-2,S_N-1-1)

где адрес размещается, начиная с 0. Эта последовательность обеспечивает деблокирование в баньян сети широкой рассылки.

КОНЦЕНТРАЦИЯ

Для того, чтобы широкополосная Баньян сеть была не блокирующей, необходимо сократить число свободных вводов, находящимися между активными вводами. Это должно быть сделано до ввода ячеек в сеть, т.е. до RAN или сразу же после DAE.

Так обратная Баньян сеть используется для концентрации активных вводов в непрерывный список [11,13]. Для получения ряда непрерывных монотонных адресов в обратной Баньян сети трассировочный адрес определяется текущими суммами на бит активности, (рисунок 4.6).

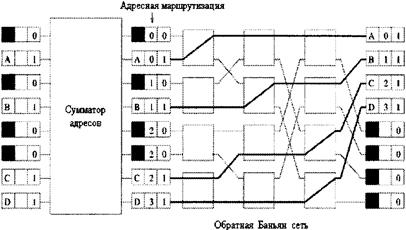
Рисунок 4.7 - Входной концентратор состоящий из сумматора адресов и обратной Баньян сети

ПРОЦЕСС ДЕКОДИРОВАНИЯ

Когда ячейка выходит из баньян сети широкой рассылки, адресный интервал в ее заголовке содержит только один адрес, т.е. по алгоритму логического разделения интервалов[13]:

min(log₂N)=max(log₂N)=Выходному адресу

Копии ячеек, из одного и того же канала широкой рассылки отмечаются CI, который определяется на выходе широкополосной Баньян сети следующим образом (рисунок 4.7):

СI=Выходной адрес-индексный эталон

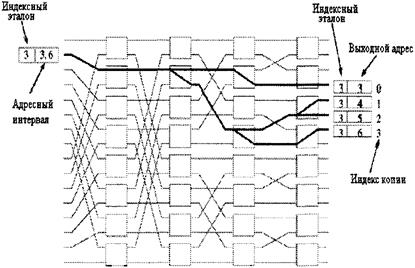
Рисунок 4.7 - Вычисление индексов копий

Индексный эталон изначально приравнивается минимуму адресного интервала. TNT (транслятор номера канала) присваивает абсолютный адрес каждой копии ячейки, и она трассируется к своему конечному назначению в последующий двухточечный коммутатор. Присвоение TN (номера канала) завершается простым табличным поиском, при котором идентификатор состоит из BCN (канала широкой рассылки) и CI (индекса копии), связанными с каждой ячейкой. Когда TNT (транслятор номера канала) получает копию ячейки, сначала он преобразует выходной адрес и IR (индексный эталон) в CI (индекс копии), а затем заменяет BCN (канал широкой рассылки) и CI (индекс копии) соответствующими TN (номерами каналов) в таблице перевода [14]. Процесс пересчета иллюстрирован на рисунке 4.8.

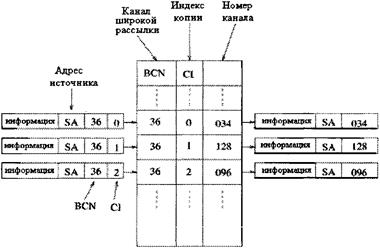
Рисунок 4.8 - Пересчет номера канала с помощью табличного поиска