Перш ніж почати цілеспрямоване формування прийому порівняння в учнів, необхідно попередньо з'ясувати рівень сформованості уміння порівнювати і розуміння сутності прийому порівняння, тобто провести діагностику.
Це можна зробити через спеціальну письмову або контрольну роботу, можна провести бесіду з учнями, обговорюючи при цьому наступні питання:
1. Що таке порівняння? Що означає “порівнювати”?
2. Навіщо проводять порівняння?
3. Яка послідовність дій при порівнянні?
Ми проводили діагностику учнів 7-9 класів Херсонської загальноосвітньої школи № 46, запропонувавши їм відповісти в письмовому виді на наступні питання:
1. Що таке порівняння? Що означає “порівнювати”?
2. Навіщо проводять порівняння?
3. Яка послідовність дій при порівнянні?
Були, також, запропоновані учням практичні пізнавальні
завдання наступного характеру:
- дати означення рівностороннього і рівнобедреного трикутника, порівняти їх;
- порівняти означення прямокутника і квадрата.
Підводячи підсумки цієї роботи і зробивши розрахунки, ми одержали наступні дані: 65,5% порівняння замінили простим описом об'єктів, що порівнювалися; 10,3% пояснили порівняння, як встановлення спільних і відмінних ознак, але і вони практично відчували труднощі при виконанні порівняння; 27,2% порівняння обмежили перерахуванням тільки відмінних ознак , а 4 учня (13,8%) зрозуміли і використовували порівняння, як знаходження подібності. Аналізуючи відповіді на поставлені питання ми прийшли до висновку, що учні не розуміють ролі порівняння в засвоєнні знань. Вони не тільки не можуть провести повне порівняння, але і поверхово володіють фактичним матеріалом, що не завжди помітно при його послідовному викладі, і взагалі завдання на порівняння для школярів незвичні й важкі.
Після діагностики необхідно створити атмосферу зацікавленості в оволодінні учнями прийомом порівняння. Для цього на етапі мотивації доцільно застосовувати різні девізи, епіграфи до уроку, наприклад, “Усе пізнається в порівнянні !”,”Без порівняння немає навчання!”
Щоб створити “сприятливий ґрунт” для переходу до наступного етапу формування прийому порівняння – осмислення суті прийому і правил його реалізації ми на наступному уроці, після письмової роботи, провели детальний аналіз її переваг і недоліків по основних структурних компонентах порівняння.
Результати здивували учнів: їм здавалося, що порівнювати так просто. І перед ними виникли питання: "А які ж правила порівняння? Що можна порівнювати, а що не можна? Чи можна скласти план і схему порівняння?" Ці і подібні питання створюють сприятливий ґрунт для осмислення суті прийому. Учні переконуються, що для порівняння об'єктів недостатньо знати окремі властивості, необхідно знати ще сутність і правило-орієнтир порівняння . Осмислення суті прийому і правила його реалізації один з найбільш важливих етапів.
Суть прийому роз'ясняється учням у виді короткого визначення: порівняння – це прийом розумової діяльності, за допомогою якого в предметах і явищах виділяються окремі ознаки, знаходяться спільні і відмінні властивості. Потім у процесі пошукової бесіди або інструктажу вводиться правило-орієнтир використання даного прийому.
Він має такий вигляд:
1. установити мету порівняння;
2. перевірити, чи відомий матеріал про об'єкти, що будуть порівнюватися;
3. виділити головні ознаки, по яких будуть порівнюватися об'єкти;
4. знайти різні властивості;
5. знайти відмінність і (або) подібність;
6. сформулювати висновок про подібність і (або) відмінність даних об'єктів відповідно до поставленої мети.
Правило-орієнтир учні повинні записати в зошитах, а вчителеві бажано завжди його мати на уроці на відеопроекторі або плакаті. Далі вчитель організує роботу з формування уміння порівнювати відповідно до правила-орієнтира.
Наприклад, пропонує порівняти ознаки подібності і ознаки рівності трикутників(мал.1):
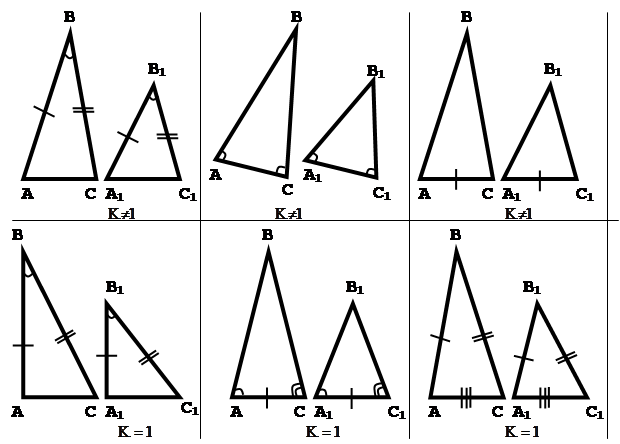
1. Встановлюємо мету порівняння: систематизація знань, раціоналізація запам’ятовування.
2. Перевіряємо, чи знаємо ми ознаки рівності і ознаки подібності трикутників.
3. Складаємо план порівняння: сформулювати теореми, ідеї доведень, з’ясувати і обґрунтувати основні знання які будемо використовувати, значення матеріалу.
4. Знаходимо спільні і відмінні риси, для цього порівнюємо формулювання теорем: вони відрізняються лише термінами “пропорціональні” і “рівні”.
Висновок: якщо замінити термін “пропорціональні” на термін ”рівні”, то із ознак подібності отримуємо відповідні ознаки рівності трикутників, тобто взяти К=1. Це доцільно застосовувати для раціонального запам’ятовування матеріалу.
Далі порівнюємо доведення ознак подібності і ознак рівності трикутників.
Для доведення всіх трьох ознак подібності трикутників застосовується загальна схема:
1. Будуємо трикутник, гомотетичний одному із даних в умові, з коефіцієнтом К= 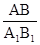 і довільним центром гомотетії.
і довільним центром гомотетії.
2. Доводимо, що отриманий при гомотетії трикутник дорівнює другому, даному в умові, за відповідною ознакою рівності трикутників.
3. Робимо висновок на підставі того, що послідовне виконання перетворення гомотетії і руху є подібність.
При доведенні всіх трьох ознак рівності трикутників застосовуються аксіоми існування трикутника, рівного даному, відкладання відрізків і кутів. У процесі доведення третьої ознаки застосовується метод від супротивного. |
Основні знання, які використовуються в обґрунтуваннях, різні. Тому доведення ознак подібності трикутників необхідно знати незалежно від доведень ознак рівності трикутників.
Висновок зроблений на основі порівняння: ознаки рівності трикутників – це окремий випадок ознак подібності, коли К=1, термінові „пропорційні” відповідає термін «рівні». Тому досить запам'ятати тільки ознаки подібності трикутників. Доведення теорем різні для ознак подібності і рівності трикутників. Призначення ознак однакове.
Багато дослідників вважають, що пізнавальні задачі дозволяють формувати в учнів досвід творчої пошукової діяльності, який іншим шляхом набути неможливо. Будь-яка пізнавальна задача або завдання для свого рішення вимагає визначеного прийому розумової діяльності або сукупності цих прийомів, що розвивають розумові здібності учнів.
Розглянемо пізнавальну задачу: „Порівняти розв’язання задач про ділення відрізка навпіл і про побудову перпендикулярної прямої”. Використовуємо питання-орієнтири, складені відповідно до правила-орієнтира прийому порівняння. Повторюємо розв’язання кожної задачі. Порівнюємо плани розв’язань і встановлюємо спільне в них: після побудови за допомогою циркуля точок А і В на прямій, розв’язання другої задачі співпадає з першою. Встановлюємо спільне в доведеннях: з рівності трикутників випливає рівність відповідних сторін або кутів. Робимо висновки: варто запам'ятовувати раціональне розв’язання задачі. Задача на побудову перпендикулярної прямої зводиться до задачі на ділення відрізка навпіл і відрізняється від неї додатковою дією – находженням на прямій точок А і В. Тому варто пам'ятати те, як розв’язувати задачу на ділення відрізка навпіл, і те, що в другій задачі потрібно спочатку за допомогою засічок із точки О знайти на прямій точки В і А. При доведенні варто шукати рівні трикутники і виділяти необхідні рівні елементи. У даному випадку порівняння дозволяє виділити головне, виступає як прийом раціонального запам'ятовування і відтворення знань.
Розглянемо прийоми формування вміння порівнювати на уроках систематизації, повторення, узагальнення знань. Вміння проміжного протиставлення можна формувати на уроках паралельного повторення, систематизації знань або вивченні понять осьової і центральної симетрії. Дії виконуються послідовно для одного і другого поняття (таблиця 4).
| Таблиця 4 | |
| Осьова симетрія (мал. 2) | Центральна симетрія (мал. 3) |
| 1) Візьмемо пряму а і точку А 2) Опустимо з точки А перпендикуляр на пряму а , 3) Продовжимо перпендикуляр в іншу півплощину 4) Відкладемо по іншу сторону від а на перпендикулярі відрізок АО=ОА1 5) Одержимо точку А1, симетричну точці А відносно прямої а Таке перетворення називається осьовою симетрією | 1) Візьмемо точки О і А 2) З'єднаємо точки А і О 3) Продовжимо півпряму по іншу сторону точки О 4) Відкладемо по іншу сторону від точки О на прямій відрізок АО=ОА1 5) Одержимо точку А1,симетричну точці А відносно точки О Таке перетворення називається центральною симетрією |
Потім учні доводять теореми про те, що симетрія на площині є рух (табл. 5).
| Таблиця 5 | ||||
| Що потрібно довести | Ідея доведення | Зв'язок з алгеброю | ||
| Осьова симетрія | Центральна симетрія | Осьова симетрія | Центральна симетрія | |
| АВ=А1В1 | Скористатися координатним методом | Розглянути рівні трикутники | У графіку парної функції Оу – вісь симетрії. Графіки взаємно обернених функцій симетричні відносно прямої у=х | У графіку непарної функції точка О (0; 0) – центр симетрії |
Далі пропонуємо учням назвати спільні і відмінні властивості понять.
Один із способів навчання умінню порівнювати – встановлення родо-видових відносин між поняттями. Невмінням учнів установлювати такі відносини пояснюється типова помилка – перенесення видових властивостей на родове поняття, що випливає через нечітке диференціювання властивостей роду і властивостей виду. Щоб запобігти такій помилці, можна запропонувати учням завдання на порівняння: якими властивостями відрізняється прямокутник від паралелограма? квадрат від ромба? квадрат від прямокутника? десятковий дріб від звичайного? пряма пропорційність від лінійної функції? бісектриса рівнобедреного трикутника, проведена з його вершини, від інших бісектрис кутів цього трикутника? які властивості загальні в названих парах понять? В чому причина того, що багато властивостей однакові? В чому причина розбіжності властивостей у порівнюваних поняттях? Яке з порівнюваних понять загальне, а яке частинне?
Без порівняння неможливе підведення під поняття, тобто розпізнавання. При цьому те поняття, до якого потрібно віднести дане поняття, виступає зі своїми властивостями як еталон. У процесі міркувань співставляються властивості „еталона” і піднесеного під нього поняття, і робиться висновок.
 Як відзначалося раніше, важливим методичним прийомом у формуванні уміння порівнювати є складання порівняльних таблиць, схем. Ця робота може виконуватися учнями як під керівництвом учителя, так і самостійно. Розглянемо порівняльну таблицю властивостей чотирикутників (табл. 6).
Як відзначалося раніше, важливим методичним прийомом у формуванні уміння порівнювати є складання порівняльних таблиць, схем. Ця робота може виконуватися учнями як під керівництвом учителя, так і самостійно. Розглянемо порівняльну таблицю властивостей чотирикутників (табл. 6).
Таблиця 6
Види чотирикутників
 –
–
Таку таблицю можна використовувати на уроках узагальнення і систематизації матеріалу в міру вивчення видів паралелограма.
Для роботи з таблицею можна давати такі завдання:
1. Порівняйте властивості паралелограма і прямокутника.
2. Які властивості в них однакові? Чому?
3. За якими властивостями відрізняється прямокутник від паралелограма? Чим це пояснити?
4. Чому в рядках 3, 4, 5, 9 властивості паралелограма, ромба, прямокутника, квадрата збігаються?
5. Чи є в паралелограма властивості, яких немає в прямокутника, ромба, квадрата? Поясніть причину.
Учні можуть скласти порівняльну таблицю властивостей перетворень подібності і руху, використовуючи як основу такі властивості подібності:
1. Це – перетворення.
2. Відстань між точками змінюється в те саме число раз.
3. Коефіцієнт подібності К 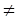 1.
1.
4. Перетворення подібності переводить прямі в прямі, півпрямі в півпрямі, відрізки у відрізки, кути – у рівні їм кути.
5. У подібних фігур відповідні кути рівні, а відповідні відрізки пропорційні.
6. Існує три ознаки подібності трикутників:
а) за рівністю двох кутів;
б) за пропорційністю двох сторін і рівності кутів між ними;
в) за пропорційністю трьох сторін.
7. Окремий випадок подібності – гомотетія.
8. Відношення периметрів подібних фігур дорівнює коефіцієнтові К.
9. Відношення площ подібних фігур дорівнює К2.
10. Послідовне виконання перетворень подібності є подібність.
11. Існує зворотне перетворення того ж виду.
12. Подібні фігури можна одержати, наприклад, за допомогою проекційної апаратури.
До складеної учнями таблиці можна запропонувати такі завдання на порівняння:
1. Якими властивостями рух відрізняється від подібності?
2. Чому рух має усі властивості подібності?
3. Яких властивостей немає в подібності в порівнянні з рухом?
4. Які, висновки можна зробити на основі порівняння?
Виконуючи ці завдання, учні вчаться проводити порівняння понять: по декількох ознаках. Цю таблицю можна використовувати при вивченні перетворень у дев'ятому класі, доповнивши її і пропонуючи додаткові завдання на порівняння.
Роботу з такими таблицями можна проводити з різними цілями: перевірити уміння порівнювати за системою ознак, формувати уміння порівнювати, повторити і систематизувати знання, встановити причинно-наслідкові зв'язки між властивостями понять, викласти матеріал блоками, раціонально заучувати і відтворювати матеріал. Учитель може організувати колективну роботу класу з таблицями, запропонувати учням самостійно заповнити половину таблиці або дати завдання скласти подібну таблицю додому, знаходячи самостійно властивості порівнюваних понять у підручнику. Ефективне складання порівняльних таблиць при встановленні міжпредметних зв'язків. У цьому випадку учні складають таблицю в класі під керівництвом вчителя або заповнюють у класі тільки одну сторону таблиці, а другу частину – додому.
Прикладами таких таблиць можуть бути: порівняльна таблиця властивостей дійсних чисел і векторів у шкільному курсі математики (табл. 7) і порівняльна таблиця зв'язку векторів у геометрії і фізиці (табл. 8).
Таблиця 7 | |
| Дійсні числа | Вектори |
1 Існують відносини рівності і нерівності
2. Є нуль
3. Існують протилежні числа:
а + (–а) = 0
4. Визначено дії додавання і віднімання чисел. Результат – число.
5. Виконуються закони додавання:
a + b = b + а,
a + (b + c) = (a + b) + c
6. Визначено дії множення і ділення чисел. Результат – число. Ділити на 0 не можна
7. Виконуються закони множення:
ab = bа,
а (bc) = (ab) c
(a + b) c= ас + bc
ab 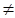 0, якщо а 0, якщо а 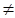 0, b 0, b 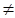 0
8. Існує взаємно однозначна відповідність між множиною дійсних чисел і точками координатної прямої
9. 0
8. Існує взаємно однозначна відповідність між множиною дійсних чисел і точками координатної прямої
9. 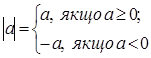 10.Напрямок на прямій
10.Напрямок на прямій
| 1. Існують відносини рівності і нерівності
2. Є нульовий вектор
3. Існують протилежні вектори:
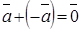 4. Визначено дії додавання і віднімання векторів. Результат – вектор.
5. Виконуються закони додавання:
4. Визначено дії додавання і віднімання векторів. Результат – вектор.
5. Виконуються закони додавання:
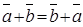
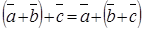 6. Визначено дію множення (ділення) вектора на число. Результат – вектор.
Визначено скалярне множення векторів. Результат – число
7. Виконуються закони множення:
6. Визначено дію множення (ділення) вектора на число. Результат – вектор.
Визначено скалярне множення векторів. Результат – число
7. Виконуються закони множення:
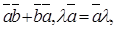
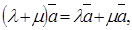
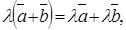
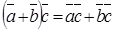 Не виконується:
Не виконується:
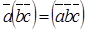
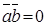 , може бути при , може бути при
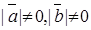 8. Існує взаємно однозначна відповідність між множиною векторів та точками координатної площини
9.
8. Існує взаємно однозначна відповідність між множиною векторів та точками координатної площини
9. 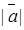 – довжина вектора – довжина вектора 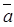 10. Напрямок на площині
10. Напрямок на площині
|
| Таблиця 8 | |
| Вектори в геометрії | Вектори у фізиці |
| Вектор – спрямований відрізок | Вектор – спрямований відрізок: сила, швидкість, прискорення, момент сил і т.п. |
Скалярне множення векторів
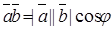
| Робота
1) при русі по похилій площині 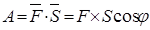 2) Ф
2) Ф 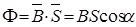 , де
Ф – магнітний потік,
В – магнітна індукція,
S – площа контуру , де
Ф – магнітний потік,
В – магнітна індукція,
S – площа контуру
|
| Обчислення довжини вектора | Знаходження значення рівнодіючої сили, швидкості та ін. |
| Розкладання вектора по координатним осям або по двох даним векторам | Розкладання сил, швидкостей, інших векторних величин по координатних осях або двом даним векторам |
| Нульовий вектор | Сума сил по замкнутому багатокутному контурі; сума сил, прикладених до центра і ваги фігури |
| Компланарні вектори | Сили, швидкості, прискорення та ін., що діють в одному або протилежних напрямках |
| Не компланарні вектори | Фізичні векторні величини, спрямовані один до одного під кутом а 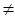 0 0
|
Крім порівняльних таблиць, при встановленні міжпредметних зв'язків можна використовувати такі завдання на порівняння:
1. Порівняйте формулу для скалярного множення векторів і для виконання роботи при русі матеріальної точки по похилій площині. Який висновок можна зробити на основі порівняння?
2. Порівняєте спосіб побудови правильного трикутника, вписаного в коло, і спосіб побудови правильного трикутника, вписаного в еліпс
3. Порівняєте способи побудови взаємно перпендикулярних діаметрів в колі і спряжених діаметрів еліпса (на уроках креслення). Що спільного в побудові?
4. Порівняйте формули, відомі з курсу фізики – 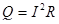 ,
, 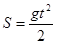 і геометрії –
і геометрії – 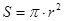 , з формулою з алгебри
, з формулою з алгебри 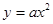 . Які висновки можна зробити на основі порівняння?
. Які висновки можна зробити на основі порівняння?
5. Порівняйте задачу „Довести, що якщо точка О є точкою перетину медіан 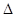 ABC, то виконується рівність
ABC, то виконується рівність 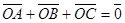 , з істотними ознаками центру ваги фігури в фізиці. Який висновок можна зробити на основі порівняння?
, з істотними ознаками центру ваги фігури в фізиці. Який висновок можна зробити на основі порівняння?
У навчальному процесі уміння порівнювати формується також при встановленні причинно-наслідкових зв'язків. З цією метою учням можна пропонувати такі завдання:
1. Побудуйте графіки функцій 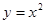 ;
; 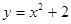 ;
; 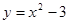 . Порівняєте їхнє положення відносно початку координат і відносно один одного. Які висновки можна зробити на основі порівняння? У чому причина такого розташування графіків?
. Порівняєте їхнє положення відносно початку координат і відносно один одного. Які висновки можна зробити на основі порівняння? У чому причина такого розташування графіків?
2. Додайте числа на координатній прямій 2 + (–4) і 3 + (–2). Порівняєте, з якої сторони від початку відліку вийшов результат у кожнім випадку. Чому в першому випадку результат ліворуч, а в другому – праворуч від точки О?
3. Порівняєте положення центрів вписаного в рівнобедрений трикутник і описаного довкола нього кіл. В чому причина такого їх взаємного розташування?
Учитель часто пропонує учням дати оцінку способу розв’язання задачі або доведення теореми з точки зору їх раціональності. Учням корисно навчитися порівнювати різні прийоми і способи заучування теорем з погляду їх раціональності й ефективності: запам'ятовувати детальне доведення, або запам'ятовувати тільки формулювання теореми й ідею доведення, або лише формулювання теореми, ідею і план доведення. Можна запропонувати одному учневі або декільком, оцінити оформлення практичних робіт, у тому числі моделей з математики, виконаних іншими учнями, оформлення розв’язання задач, доведень теорем і вибрати найбільш раціональне і гарне оформлення.
Прийом порівняння можна формувати, створюючи на уроках проблемні ситуації. Так, перед вивченням теореми Фалеса учням можна запропонувати практичну роботу: „На сторонах кута відкласти кілька рівних відрізків. Провести через них паралельні прямі до перетину їх з іншою стороною кута. Порівняти довжини отриманих відрізків на іншій стороні кута. Чи випадкова рівність довжин отриманих відрізків? У чому причина такої рівності? Чи можна строго довести істинність заміченої закономірності в загальному випадку?”
Інші приклади: „Майстер при виготовленні табурета, щоб перевірити, чи не буде він хитатися, натягає на кінці його ніжок пересічні мотузки. Новорічну ялинку ставлять у хрестовину. Для стійкості столу його ніжки іноді з'єднують хрестовиною”. Учням пропонується порівняти ці ситуації, знайти в них спільне, висунути гіпотезу на основі порівняння.
На уроках математики можна залучати учнів до порівняння різних випадків взаємного положення геометричних фігур.
Уміння порівнювати формується при пошуку зв'язків за аналогією. Порівняння тут виступає як основа прийому аналогії. Без порівняння й аналогії неможливий перенесення способу розв’язання однієї задачі на іншу того ж типу, висунути припущення про закономірність, визначених властивостей досліджуваних фігур. У курсі геометрії порівняння разом з аналогією широко застосовується при вивченні векторів і декартових координат на площині.
Багато аналогічних задач планіметрії корисно розглядати в порівнянні.
Учні при цьому не лише повторюють, систематизуючи раніше вивчений матеріал, але і використовують його як базу для вироблення нових умінь і навичок. Вони вчаться знаходити глибокі зв'язки між різними розділами геометрії, переносити раніше сформовані знання уміння і навички в нові умови. Наприклад, паралельно можна розглянути рішення задачі „Складіть рівняння прямої, що проходить через точки А(–1; 1); В(1;0)” і задачі з курсу дев'ятого класу „Складіть рівняння площини, що проходить через точки А (1; 0; 0); В(0; 2; 0); С(0; 0; 3)”.
У вчителя є багато можливостей для формування вміння порівнювати на різному навчальному матеріалі геометрії й у різних методичних ситуаціях. Учителі математики формують уміння порівнювати на уроках геометрії й алгебри паралельно, Важливо наполегливо рекомендувати учням активно застосовувати прийом порівняння при вивченні різних шкільних дисциплін.
ВИСНОВКИ
Проведена робота з досліджуваної теми дозволяє зробити наступні висновки:
1. Було проаналізовано стан проблеми формування прийомів мислення учнів у психолого-педагогічній і методичній літературі, а також шкільній практиці.
2. Провівши контрольну роботу з учнями основної школи, ми визначили їхній рівень сформованості та вміння порівнювати при навчанні математики.
3. З метою виявлення методичних умов ефективної організації процесу формування в учнів вміння порівнювати було проаналізовано методичну літературу, проведено бесіди з вчителями-предметниками, учнями 7-9 класів.
4. На основі отриманих результатів ми розробили і експериментально перевірили методики та завдання цілеспрямованого формування вміння порівнювати при навчанні математики в учнів 7-9 класів, результати виявилися втішними.
Порівняння зв'язане в навчальному пізнанні з всіма основними прийомами розумової діяльності, особливо з виділенням головного й узагальненням. Порівняння починається з аналізу і виділення головного; якщо учні опанували умінням виділяти головне, прийом порівняння формується значно швидше і на більш високому рівні. Сформований прийом порівняння дозволяє приступити до цілеспрямованого формування уміння узагальнювати; крім того, будь-яке порівняння повинно закінчуватися узагальненням, тобто тією добавкою до старих знань, заради якої відбувається порівняння. Застосування прийому порівняння сприяє досягненню позитивних результатів у навчанні і розвитку, якщо воно вводиться цілеспрямовано, усвідомлено, з урахуванням характеру матеріалу, порівнюваних обсягів, віку і рівня розвитку учнів.
 СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
1. Бабанский 10.К. Оптимизация учебно-воспитательного процесса.-М.Просвещение,1982.
2. Бевз Г. П. Методика розв'язування алгебраїчних задач. – К.: Рад. шк., 1975 – 240 с.
3. Бевз Г. П. Математика, 6 кл. – К.: Вежа, 2002. – 224 с.
4. Бевз Г. П. Алгебра: Підруч. для 7-9 кл. - К.: Освіта, 2001. - 303 с.
5. Богоявленский Н. Формирование приёмов умственной работы учащихся как путь развития мышления и активизации учения //Вопросы психологии.-1962.-М.-С.7 4-82.
6. Епишев О. Б., Крупич В. И. Учат школьников учиться математике: Формирование приемов учебной деятельности: Кн. для учителя. – М.: Просвещение, 1990. - 126 с.
7. Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статистика: Навч.-метод, посіб. – К.: КНЕУ, 2002. – 303 с
8. Зак А. З, Как определить уровень развития мышления школьника. – М.: Знание. - 1982. - 96 с,
9. Зеккер Л.М. Психологические процессы.: Изд-во Ленинград.ун-та, 1976.-342 с.
10. Выготский Л.С. Собр.соч. т.1-6.М.,1982-1384.
11. Груденов Я. И. Совершенствование методики работы учителя математики: Кн. для учителя. – М.: Просвещение, 1990. – 223 с.
12. Гусев В. А., Иванов А. И., Шаболин О. Д. Изучение величин на уроках математики и физики в средней школе. – М.: Просвещение, 1991. – 79 с.
13. Епишева О.Б.Друпич З.Л. Учить школьников учиться математике.-М.просвещение, I99C.-128 с.
14. Земляков. Геометрия в 9 классе.-U.гПросвещеяие,1988.–с.208.
15. Земляков А.Н.Геометрия в 9 классе.-М.: Просвещение, 1986.-2С8с.
16. Кабанова-Меллер Е.Н.Приемы учебной работы и овладение ими (в условиях развивающего обучения)//Вопросы психологии.-I98C.-C.145-I5C.
17. Кабанова-Меллер Е.Н.Роль образа в решении задач//Вопросы психологии. C.122-131C
18. Кабанова-Меллер В.И. Формирование приёмов умственной деятельности и умственное развитие учащихся.-М.:Просвещение,. 1968.-288с.
19. Калмыкова 3. И. Продуктивное мышление как основа обучаемости. – М.: Педагогика, 1981. - 200 с.
20. Калмыкова 3. И. Психологические принципы развивающего обучения. – М.: Знание, 1979. - 48 с.
21. Карнацевич Л. С, Мартынова М. П., Неменко В. М. Кабинет математики в школе. – К.: Рад. шк., 1978. – 127 с.
22. II.Крупская Н.К.Методические заметки. Педагог.соч. в десяти томах, т.З.-М.:Лзд-во АПН РСФСР, 1959.– с.552-560.
23. Менчинская Н.А. Мишление в процессе обучения//исследование мышления в советской психологии.-М., 1966.-с.349-357.
24. Методика викладання математики: Практикум / За ред. Г. П. Бевза. — К.: Вища шк. Головне вид-во, 1981. – 199 с.
25. Методика викладання математики: Наук.-метод, зб. / За ред. І. Є.
26. Методика преподавания математики в средней школе: Общая методика / В. А. Оганесян, ІО. М. Колягин, Г. Я. Луканкин, В. Я. Соминський. – 2-е изд., перераб. и доп. – М.: Просвещение, 1980.- 367 с.
27. Методика преподавания математики в средней школе: Частные методики: Учеб. пособие для физ.-мат. фак. пед. ин-тов / Ю. М. Колягин, Г. Я. Луканкин, Е. Л. Макрушин и др. – М.: Просвещение, 1977. – 480 с.
28. Методика преподавания математики в средней школе: Общая методика./Сост.: В. С. Черкасов, А. А. Столяр. – М.: Просвещение, 1985. – 336 с.
29. Методика преподавания математики в средней школе: Частная методика/Сост. В. И. Мишин. – М.: Просвещение, 1987. – 414 с.
30. Методика розв'язання задач на побудову/За ред. О. М. Астряба, О. С. Смо-горжевського. – К.: Рад. шк., 1962. – 387 с.
31. Мишин В.И. Методика преподавания математики в средней школе.-М.:Просвещение,1987.
32. Осинская З.Н. Активизация познавательной деятельности учащихся на уроках математики в 9-IC классах. Киев: Рад.школа, 119C.-143с.
33. Осинская В.Н.Формирование умственной культуры учащихся в процессе обучения математике.-К.:Рад.школа,1989.
34. Паламарчук В.Ф. Школа учит мыслить.-М.:Просвещение,1979.
35. Погорелов А.В. Геометрия. Учебное пособие дал 6–10 классов средней школы.-Ж. : Просведение, 1988.-ЗСЗ с.
36. Рубинштейн С.А.Принципы пути развития психологии. М.:Лзд-во АН СССР, 1958,-1.47 с.
37. Самостоятельная деятельность учащихся при обучений математики (формирование умений самостоятельной работы):Сб.статей (Состаз. С.И.Демидова, О.деяйщева)т И.:Просвещение,1985.-191 с. (Е-ка учителя математики).
38. Слепкань З.Л. Зсяхолого-педагогические основы обучения математике:Метод.пособие.-Киев:Рад.школа,1983.-192 с.
39. Талызина Н.5. Управление процессом усвоения знании.-М.:Изд-во Моск.ун-та,1975.-343с.
40. Ридман Л.М. Учитесь учиться математике.-М.просвещение,1985.
41. Эрдниев I.M., Эрдниев Б.П. Укрупнение дидактических единиц в обучении математике.-М.:Просвещение,198С.-255с.
Дата: 2019-07-24, просмотров: 375.