Математики
Порівняння в навчанні – це розумова операція, за допомогою якої встановлюються риси подібності і відмінності між визначеними предметами і явищами.
Пізнання будь-якого предмету і явища починається з того, що ми відрізняємо його від інших предметів і встановлюємо його подібність з родинними предметами. У цьому виявляються дві основні форми, у яких здійснюється порівняння: співставлення і протиставлення.
Протиставлення – форма порівняння, спрямована на з'ясування відмінного в предметах і явищах при виділенні істотних ознак і властивостей.
Співставлення – форма порівняння, спрямована на виділення істотних властивостей, загальних для ряду об'єктів.
У розумовій діяльності учня протиставлення і співставлення як форми порівняння виконуються в єдності і є засобом аналізу і синтезу досліджуваних понять, фактів , предметів. Але в навчальному процесі ці розумові операції найчастіше здійснюються послідовно.
Надзвичайно важлива роль порівняння при формуванні понять, узагальнені і систематизації знань. Порівняння - засіб зв'язку нових і раніше засвоєних знань, матеріалу підручника й особистого досвіду учнів.
У математиці важливо уміти встановлювати відмінності між близькими родинними поняттями (наприклад, між раціональними й ірраціональними числами, правильними і неправильними дробами) і подібність між віддаленими поняттями (трикутником і тетраедром).
По ступеню повноти розрізняють часткові і повні порівняння. Суть часткового порівняння у встановленні тільки подібного або тільки відмітного. Якщо в об'єктах знаходять ознаки подібності, то це зіставлення, якщо шукають відмінність – це протиставлення.
Повне порівняння вимагає встановлення подібності і відмінності. Часткове порівняння ефективне на етапах сприйняття й осмислення знань, дозволяє глибше усвідомити особливе в досліджуваному матеріалі, зрозуміти його зв'язок з раніше засвоєними знаннями.
Пізнавальні завдання на протиставлення можуть бути такими :
1. Чим відрізняється об'єкт А від об'єкта В?
2. Яких властивостей немає в об'єкті А в порівнянні з об'єктом В?
3. Якими додатковими властивостями володіє об'єкт А в порівнянні з об'єктом В?
4. Чим відрізняються формулювання...?
Приклади:
1. Чим відрізняється бісектриса трикутника від його медіани?
2. Які додаткові властивості має рівносторонній трикутник в порівнянні з рівнобедреним?
3. Чим відрізняється ромб від квадрата; ромб від паралелограма? Які властивості в них спільні?
4. Які додаткові властивості має прямокутник в порівнянні з паралелограмом?
З метою узагальнення матеріалу учням пропонуються завдання на співставлення об'єктів (находження спільного).
Приклади:
1. Які спільні властивості має симетрія, паралельний перенос, поворот? В чому причина загальності даних властивостей?
2. Що спільного в доведенні ознаки паралельності прямої і ознаки паралельності площин?
Повне порівняння ефективне на етапах узагальнення і систематизації знань.
Приклади:
1. Порівняйте ознаки рівності трикутників з ознаками подібності трикутників. Які висновки можна зробити на основі порівняння?
2. Порівняйте основні припущення про довжини і площі. Які висновки з цього можна зробити?
По способах здійснення розрізняють порівняння паралельні, послідовні відстрочені.
Паралельні порівняння застосовуються при одночасному вивченні взаємопов’язаних понять, теорем і задач, при викладі матеріалу блоками.
В дев’ятому класі доцільно в порівнянні паралельно вивчати поняття паралельних, мимобіжних та прямих, що перетинаються (таблиця 1).
Таблиця 1
| Прямі на площині і в просторі | ||
| Паралельні | Ті, що перетинаються | Мимобіжні |
| 1. Не мають спільних точок 2. Лежать в одній площині | 1. Мають одну спільну точку 2. Лежать в одній площині | 1. Не мають спільних точок 2. Не лежать в одній площині |
Доцільні завдання такого змісту:
1. Які ознаки спільні у паралельних прямих і прямих, що перетинаються; у паралельних і мимобіжних?
2. Які відмінні ознаки у паралельних і мимобіжних прямих?
Виконання таких завдань, по-перше, формує вміння аналізувати, порівнювати і, по-друге, попереджує типову помилку, коли учні в означенні мимобіжних прямих називають тільки першу ознаку.
Послідовне порівняння полягає в тому, що новий об'єкт порівнюється з раніше вивченим. Порівняння сприяє встановленню більш глибоких зв'язків раніше вивченого і нового матеріалу, полегшує засвоєння знань, допомагає побачити аналогії.
Розглянемо приклад послідовного порівняння під час вивчення у восьмому класі поняття рівності фігур за допомогою руху. Учні повторюють відомі їм означення рівності трикутників: 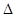 АВС=
АВС= 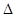 А1В1С1, якщо АВ=А1В1, ВС=В1С1, АС=А1С1,
А1В1С1, якщо АВ=А1В1, ВС=В1С1, АС=А1С1, 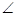 А=
А= 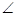 А1,
А1, 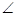 В=
В= 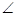 В1,
В1, 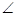 С=
С= 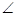 С1. Вчитель дає нове означення рівності фігур за допомогою руху. Порівнюючи ці означення, учні виділяють істотні ознаки між ними. Різні означення рівності трикутників – це наслідок відмінності їх теоретичних обґрунтувань. А щоб учні впевнилися в тотожності цих означень при їх різних формулюваннях, на прикладі з трикутниками доводиться, що із одного означення випливає інше і навпаки.
С1. Вчитель дає нове означення рівності фігур за допомогою руху. Порівнюючи ці означення, учні виділяють істотні ознаки між ними. Різні означення рівності трикутників – це наслідок відмінності їх теоретичних обґрунтувань. А щоб учні впевнилися в тотожності цих означень при їх різних формулюваннях, на прикладі з трикутниками доводиться, що із одного означення випливає інше і навпаки.
Відстроченими називаються порівняння об'єктів, що вивчалися на різних уроках, значно віддалених один від одного в часі.
У практиці навчання математики найбільш поширене послідовне порівняння. Але, оскільки вчителі все більш широко практикують вивчення матеріалу блоками, то часто застосовується і паралельне порівняння при одночасному вивченні взаємопов’язаних понять, теорем, задач. Завдяки використанню в навчанні послідовного порівняння і порівняння – протиставлення у свідомості школярів загальмовуються помилкові і закріплюються правильні тимчасові зв'язки, диференційовано встановлюються поняття, правила і закони.
Якщо порівняння різних предметів (фактів, явищ) здійснюється не по одній ознаці, а знаходять спільне і відмінне по різним ознакам і в різних напрямках, то таке порівняння називається комплексним.
Приклади:
o Чотирикутники порівнють за числом пар паралельних сторін;
o дроби відрізняють по відношенню величин чисельника і знаменника;
o додавання дійсних чисел і додавання векторів порівнють за виконуваністю законів додавання.
Порівняння однорідних предметів по одній ознаці веде до класифікації, розподілу об'єктів на дві групи, наприклад: функції – періодичні і неперіодичні, зростаючі й спадні.
Як і будь-який прийом розумової діяльності, порівняння має свій предмет, супроводжує визначену мету і пропонує свої шляхи реалізації в процесі навчання.
При вивченні математики предметом порівняння можуть бути об'єкти навколишньої дійсності, поняття, ознаки, результати дослідів, теореми і їх доведення, структури задач і методи їх розв’язань, операційний склад алгоритмів різних дій, способи навчальної роботи, а також факти, процеси, етапи роботи. На уроках учням пропонують порівнювати: взаємне положення прямих у=5х и у=5х-7 на координатній площині; істотні і несуттєві, доказові і характеристичні ознаки понять; способи роботи з метою вибору більш раціонального (наприклад, самоконтроль шляхом припущень або шляхом складання зворотної задачі).
Порівнюючи, учні повинні чітко розуміти, з якою метою це робиться. На уроці цілі порівняння часто називає сам учитель; при цьому необхідно викликати в учнів інтерес до оволодіння даним прийомом мислення.
Мета порівняння в навчальному процесі різноманітна: узагальнення і систематизації знань, виділення в них головного, істотного, пошук загальних ознак при формуванні понять; пошук аналогій у навчальному матеріалі; пошук закономірностей індуктивним шляхом; висування гіпотез; установлення міжпредметних зв'язків у навчальному матеріалі й у способах його вивчення; запобігання помилок за аналогією; побудова системи аналогів даного об'єкта; запобігання підміни істотних властивостей поняття несуттєвими властивостями; виділення істотного і несуттєвого в умові задачі, узагальнення її структури й усвідомлення границь варіації її умови усередині даного типу задач. Порівняння є одним з раціональних прийомів заучування і відтворення матеріалу, але, на жаль, недостатньо застосовується при вивченні математики. Без порівняння неможливий перенос способу рішення однієї задачі на іншу – аналогічну.
Інтерес до порівняння виникає в учнів в міру того, як вони усвідомлюють його роль в успішному оволодінні знаннями, починають розуміти, що цей прийом має загальнопізнавальний характер, що , навчивши порівнювати на уроках математики, вони зможуть використовувати порівняння при вивченні інших шкільних предметів, у життєвих ситуаціях. У навчальному процесі порівняння служить одним із засобів об'єднання матеріалу в блоки. На уроці порівняння виступає як самоціль. Воно найчастіше є основою більш складних прийомів розумової діяльності або способом раціонального заучування матеріалу.
Існує ряд дидактичних вимог до використання прийому порівняння в навчальному процесі:
1. Порівнювати треба тільки однорідні предмети.
Недоцільне порівняння, наприклад, таких понять, як “відрізок” і “точка”, “ромб” і “коло”.
2. Спільне між об'єктами порівняння можна встановлювати лише тоді, коли між ними є якась відмінність.
Різницю між об'єктами можна встановлювати тільки при наявності в них визначеної подібності.
Школярі не завжди усвідомлюють відносини між родинними поняттями, як відносини частинного і загального. Саме в такому випадку доречно порівнювати ці поняття за допомогою питань, наприклад: Що спільного і відмінного у функцій і послідовностей? Яке з цих понять є частинним випадком стосовно іншого і чому?
3. Порівнювати предмети слід за тими ознакам, що мають важливе, істотне значення.
Необхідно враховувати, що до порівняння учні не знають про істотність ознак. Крім того, істотність ознак також визначається в порівнянні. Тому вчитель спочатку підказує, по яких важливих ознаках варто проводити порівняння. Так при порівнянні задач варто звертати увагу на дані умов, характер зв'язку між даними і шуканими, тому що саме це визначає спосіб розв’язання. Зовнішня подібність або відмінність смислу задач не має істотного значення для способу їхнього рішення. У задач одного типу є загальне в істотному: структурі, умові, зв'язках між даними умови і шуканих величин – і розбіжність між несуттєвим у їхніх умовах і рішеннях.
Психологи установили, що учні легше знаходять у порівнюваних об'єктах або тільки спільне, або тільки відмінне. Присутність в порівнюваних об'єктах різного і подібного (загального) виявляється для учнів більш важкою справою, тому що вимагає розумової роботи в двох напрямках одночасно. Школярі затрудняються порівнювати процеси міркувань при виконанні вправ на знаходження процента від числа, числа за його процентом та процентного відношення двох чисел.
4. Порівнювати треба під певним кутом зору. У навчанні порівняння завжди цілеспрямоване. Ті самі об'єкти можуть мати подібність, якщо їх розглядати з однієї позиції, і можуть відрізнятися, якщо змінити “кут зору”. Наприклад, формули для обчислення площ паралелограма і трапеції зовні не мають нічого загального, але способи їхніх доведень однакові: суть виведення формул полягає в тому, що фігура перетвориться в такі фігури (або таку фігуру), площі яких заздалегідь відомі.
Прийоми розумової діяльності формуються стихійно або цілеспрямовано. Учні під керівництвом учителя порівнюють об'єкти за спільними, відмінними, та за тими й іншими ознаками одночасно. Але якщо при цьому сутності прийому, його операційному складові не приділяється належної уваги, то навіть встигаючі учні не можуть цілком назвати подібні і відмінні властивості понять, зробити план, схему порівняння.
Ю.К.Бабанський писав, що для успішного оволодіння будь-яким загальнонавчальним умінням або навичкою необхідно забезпечити наступний ланцюжок дій учнів:
- прийняття задачі, що вимагає оволодіння відповідним умінням і навиками;
- усвідомлення необхідності опанувати навиками, мотивація діяльності;
- засвоєння змісту навиків, послідовності і характеру дій, операцій, що необхідні для оволодіння цим навиком;
- виконання практичних дій, операцій, вправ по відпрацьовуванню навиків;
- поточний самоконтроль за ступенем оволодіння навиками;
- коригуючі дії спрямовані на відпрацювання навиків;
- застосування умінь і навичок у типових ситуаціях;
- застосування умінь і навичок у нестандартних ситуаціях;
- поглиблення і подальша автоматизація навиків шляхом використання його в повсякденній практичній діяльності [1 с.95].
Для вчителя, названий ланцюг дій виступає як методологічна схема діяльності по формуванню будь-якого загальнонаукового уміння, зокрема, прийому порівняння. Звичайно вчитель, приступаючи до формування уміння порівнювати, насамперед з'ясовує, що знають учні про цей прийом, які помилки допускають при порівнянні, тобто які рівні сформованості цього уміння в різних школярів, як вони розуміють сутність прийому порівняння, його операційний склад, мету застосування. Можна провести бесіду або письмову роботу на порівняння, запропонувавши учням наступні питання:
1. Що таке порівняння? Що означає “порівняти”?
2. Навіщо проводять порівняння?
3. Яка послідовність дій при порівнянь?
Практичні пізнавальні завдання, наприклад: порівняти способи розв’язання двох задач або доведення двох теорем, також допомагають виявити рівні оволодіння школярами умінням порівнювати. При цьому ніяких вказівок, плану, правил порівняння вчитель не дає.
Аналізуючи відповіді учнів на згадані питання, я прийшла до наступних висновків: багато учнів не могли назвати послідовності дій при порівнянні; не розуміють ролі порівняння в засвоєнні знань; взагалі, завдання на порівняння для учнів 7-9 класів незвичні й важкі.
Дата: 2019-07-24, просмотров: 469.