Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Функции и их графики.

1. Сформулируйте определение графика функции.
2. Что называется областью определения функции?
3. Как найти область определения функции по ее графику?
4. Что называется областью значений функции?
5. Как найти область значения функции по ее графику?
6. Какая функция называется четной?
7. Какая функция называется нечетной?
8. Как исследовать функцию на четность (нечетность) по ее графику?
9. Что такое нули функции?
10. Как определить нули функции по ее графику?
11. Закончите фразу: «Промежутки знакопостоянства – это…»
12. Как найти промежутки знакопостоянства функции по ее графику?
13. Что такое точка экстремума функции? Какие виды точек экстремумов вам известны?
14. Что такое экстремумы функции? Какие виды экстремумов вам известны?
15. Какие виды монотонности функции вам известны?
16.  Закончите фразу: «Промежутки монотонности – это…»
17. Как найти промежутки монотонности функции по ее графику?
18. Сформулируйте определения наибольшего и наименьшего значений функции.
19. Как найти наибольшее и наименьшее значения функции по ее графику?

 

Тема № 2.

Производная и ее применение

1. Сформулируйте определение производной функции в точке.
2. Закончите фразу: «Чтобы найти производную алгебраической суммы нескольких функций необходимо…»
3. Закончите фразу: «Чтобы найти производную произведения двух функций необходимо…»
4. Закончите фразу: «Чтобы найти производную отношения двух функций необходимо…»
5. Как при дифференцировании поступают с коэффициентами?
6. Что такое критическая точка функции?
7. Как при помощи производной определить характер монотонности функции?
8. Может ли критическая точка функции не являться точкой экстремума?
9. Как при помощи производной найти точку максимума (минимума) функции?
10. Перечислите известные вам производные алгебраических функций.

 

Тема № 3.

Тригонометрические функции

1. Какой поворот в математике называется поворотом на положительный (отрицательный) угол?
2. Сформулируйте определение угла в 1 радиан.
3. Воспроизведите алгоритм перехода от радианной меры угла к градусной мере и обратно.
4. Сформулируйте определения следующих тригонометрических функций: синуса, косинуса, тангенса и котангенса.
5. Перечислите значения синуса, косинуса, тангенса и котангенса 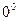, , 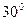,  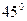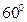и .
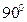6. Повторите мнемическое правило формул приведения.
7. Перечислите свойства следующих тригонометрических функций: синуса, косинуса, тангенса и котангенса

- Область определения

- Область значений

- Четность (нечетность)

- Нули функции

- Наименьший положительный период

- Промежутки монотонности

- Экстремумы функции (если они есть)

- Наибольшее и наименьшее значения функции (если они есть)

1. Сформулируйте определения обратных тригонометрических функций: арксинуса, арккосинуса и арктангенса.
2. Перечислите свойства обратных тригонометрических функций: арксинуса, арккосинуса и арктангенса

- Область определения

- Область значений

- Четность (нечетность)

- Нули функции

- Характер монотонности

- Экстремумы функции (если они есть)

- Наибольшее и наименьшее значения функции (если они есть)

1. Перечислите простейшие тригонометрические уравнения и условия, при которых они имеют решение.
2. Сформулируйте общее решение каждого из простейших тригонометрических уравнений.

 

Тема № 4.

Многогранники

1. Закончите фразу: «Двугранный угол – это…»
2. Что такое грань двугранного угла?
3. Что такое ребро двугранного угла?
4. Какая фигура называется трехгранным углом?
5. Что такое многогранный угол?
6. Что такое многогранник?
7. Какой многогранник называется выпуклым?
8. Что такое призма?
9. Какая призма называется прямой?
10. Какая призма называется правильной?
11. Что такое высота призмы?
12. Что такое диагональ призмы?
13. Что называется диагональным сечением призмы?
14. Чем образована боковая поверхность призмы?
15. Какой многогранник называе6тся параллелепипедом?
16. Сформулируйте определения прямого и прямоугольного параллелепипедов.
17. Какими фигурами являются диагональные сечения различных видов параллелепипедов?
18. Что такое куб?
19. Какой многогранник называется пирамидой?
20. Что такое правильная пирамида?
21. Сформулируйте определение апофемы.
22. Какая пирамида называется усеченной?
23. Какими фигурами являются диагональные сечения различных видов пирамид?
24. Какая пирамида называется тетраэдром?

 

Тема № 12.

Тела вращения

1. Какое тело называется цилиндром?
2. Что такое образующая цилиндра?
3. Что такое радиус цилиндра?
4. Какой цилиндр называется равносторонним?
5. Что такое ось цилиндра?
6. Какой фигурой является осевое сечение цилиндра?
7. Какой фигурой является сечение цилиндра плоскостью, параллельной плоскости основания?
8. Какая плоскость называется касательной плоскостью цилиндра?
9. Сформулируйте определения призм, описанных около и вписанных в цилиндр.
10. Какое тело вращения называется конусом?
11. Какой конус называется прямым?
12. Что такое радиус конуса?
13. Какой конус называется равносторонним?
14. Что такое ось конуса?
15. Какой фигурой является осевое сечение конуса?
16. Какой фигурой является сечение конуса плоскостью, параллельной плоскости основания?
17. Какая плоскость называется касательной плоскостью конуса?
18. Сформулируйте определения пирамид, описанных около и вписанных в конус.
19.  Что такое шар?
20. Сформулируйте определение сферы.
21. Что называют диаметром шара?
22. Что называют радиусом шара?
23. Какие точки шара называются диаметрально противоположными?
24. Сформулируйте определение диаметральной плоскости шара.
25. Что такое большой круг?
26. Что такое большая окружность?
27. Какая плоскость называется касательной плоскостью шара? Каким свойством она обладает?
28. Сформулируйте определения многогранников, описанных около и вписанных в шар.

 

Тема № 13.

Объемы многогранников

1. Какое тело называют простым?
2. Закончите фразу: «Равные тела имеют…»
3. Закончите фразу: «Если тело разбито на части, являющиеся простыми телами, то его объем равен…»
4. Закончите фразу: «Объем куба, ребро которого равно 1, равен…»
5. Как вычислить объем любой призмы?
6. Как вычислить объем прямоугольного параллелепипеда?
7. При каком условии две пирамиды с равными площадями оснований имеют равный объем?
8. По какой формуле вычисляется объем любой пирамиды?
9. Каким образом вычисляется объем усеченной пирамиды?
10. Закончите фразу: «Объемы двух подобных тел относятся, как…»

 

Тема № 14.

Функции и их графики.

1. Сформулируйте определение графика функции.
2. Что называется областью определения функции?
3. Как найти область определения функции по ее графику?
4. Что называется областью значений функции?
5. Как найти область значения функции по ее графику?
6. Какая функция называется четной?
7. Какая функция называется нечетной?
8. Как исследовать функцию на четность (нечетность) по ее графику?
9. Что такое нули функции?
10. Как определить нули функции по ее графику?
11. Закончите фразу: «Промежутки знакопостоянства – это…»
12. Как найти промежутки знакопостоянства функции по ее графику?
13. Что такое точка экстремума функции? Какие виды точек экстремумов вам известны?
14. Что такое экстремумы функции? Какие виды экстремумов вам известны?
15. Какие виды монотонности функции вам известны?
16.  Закончите фразу: «Промежутки монотонности – это…»
17. Как найти промежутки монотонности функции по ее графику?
18. Сформулируйте определения наибольшего и наименьшего значений функции.
19. Как найти наибольшее и наименьшее значения функции по ее графику?

 

Тема № 2.

Производная и ее применение

1. Сформулируйте определение производной функции в точке.
2. Закончите фразу: «Чтобы найти производную алгебраической суммы нескольких функций необходимо…»
3. Закончите фразу: «Чтобы найти производную произведения двух функций необходимо…»
4. Закончите фразу: «Чтобы найти производную отношения двух функций необходимо…»
5. Как при дифференцировании поступают с коэффициентами?
6. Что такое критическая точка функции?
7. Как при помощи производной определить характер монотонности функции?
8. Может ли критическая точка функции не являться точкой экстремума?
9. Как при помощи производной найти точку максимума (минимума) функции?
10. Перечислите известные вам производные алгебраических функций.

 

Тема № 3.

Тригонометрические функции

1. Какой поворот в математике называется поворотом на положительный (отрицательный) угол?
2. Сформулируйте определение угла в 1 радиан.
3. Воспроизведите алгоритм перехода от радианной меры угла к градусной мере и обратно.
4. Сформулируйте определения следующих тригонометрических функций: синуса, косинуса, тангенса и котангенса.
5. Перечислите значения синуса, косинуса, тангенса и котангенса 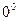, , 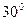,  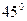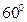и .
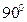6. Повторите мнемическое правило формул приведения.
7. Перечислите свойства следующих тригонометрических функций: синуса, косинуса, тангенса и котангенса

- Область определения

- Область значений

- Четность (нечетность)

- Нули функции

- Наименьший положительный период

- Промежутки монотонности

- Экстремумы функции (если они есть)

- Наибольшее и наименьшее значения функции (если они есть)

1. Сформулируйте определения обратных тригонометрических функций: арксинуса, арккосинуса и арктангенса.
2. Перечислите свойства обратных тригонометрических функций: арксинуса, арккосинуса и арктангенса

- Область определения

- Область значений

- Четность (нечетность)

- Нули функции

- Характер монотонности

- Экстремумы функции (если они есть)

- Наибольшее и наименьшее значения функции (если они есть)

1. Перечислите простейшие тригонометрические уравнения и условия, при которых они имеют решение.
2. Сформулируйте общее решение каждого из простейших тригонометрических уравнений.

 

Тема № 4.

Степень с рациональным показателем

1. Сформулируйте определение степени с рациональным показателем.
2. Сформулируйте определение корня п–ой степени.
3. Перечислите свойства степеней с рациональным показателем.
4. Перечислите свойства корней п–ой степени.
5. Выясните, при каких значениях а уравнение 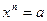не имеет корней (п – четное).
6. Выясните, при каких значениях а уравнение 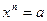 имеет 1 корень (п – четное).
7. Выясните, при каких значениях а уравнение 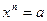 имеет 2 корня (п – четное).
8. Выясните, сколько корней имеет уравнение 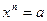 при различных значениях а (п – нечетное).

 

Тема № 5.