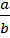sin A = ;        tg A = ;         cos A = ;       ctg A = ;

Формулы для вычисления радиусов вписанной ( r ) и описанной ( R ) окружностей.

R = 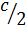= m;    r = 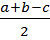, m –медиана, проведённая из вершины прямого угла .

Формула площади.         S = .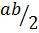

Произвольный треугольник.

Определение вида треугольника по его сторонам:

- если 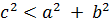, то треугольник остроугольный;

- если 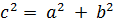, то треугольник прямоугольный;

- если 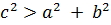, то треугольник тупоугольный; где c –наибольшая сторона

Соотношения между сторонами и углами.

1. Сумма внутренних углов треугольника равна 180 .

2. Сумма двух сторон треугольника больше его третьей стороны (неравенство треугольника).

3. Против большей стороны треугольника лежит больший угол и,наоборот, против большего угла лежит большая сторона.

4. a ² = b ² + c ² – 2 bc 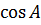 (теорема косинусов).

5. 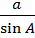 =  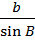=  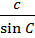= 2 R (теорема синусов).

Свойства медиан.

1. Медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.

2. Медиана треугольника делит его на два равновеликих треугольника

3. Три медианы треугольника делят его на шесть равновеликих треугольников.

4. m = 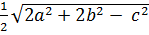, где m – медиана, проведённая к стороне с.

Свойства биссектрис.

1. Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности вписанной в треугольник.

2. Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам.

Свойство высот.

Прямые, содержащие высоты треугольника, пересекаются в одной точке.

Свойство серединных перпендикуляров.

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника.

Свойства средней линии треугольника.

1. Средняя линия треугольника параллельна стороне треугольника и равна её половине.

2. Средняя линия треугольника делит пополам любой отрезок, соединяющий вершину треугольника с какой-либо точкой основания.

Формулы для вычисления площади.

1. S = ;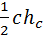

2. S = ;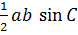

3. S = 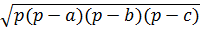 где p - полупериметр(формула Герона);

4. S = 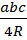, где R – радиус описанной окружности;

5. S = pr , где r – радиус вписанной окружности.

Формулы для вычисления радиусов вписанной ( r ) и описанной ( R ) окружностей.

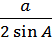    R = 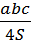,     R = ,         r = .

Пропорциональные площади треугольников.

1. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

2. Если два треугольника имеют равные углы, то их площади относятся как произведения сторон, заключающих эти углы.

3. Если два треугольника имеют общее основание (или равные основания), то их площади относятся как высоты, проведённые к этому основанию.

4. Если два треугольника имеют общую высоту (или равные высоты), то отношение их площадей равно отношению оснований.

Четырёхугольники.